Verifikationsfälle – Modalanalysen
Modalanalyse für einen Auslegerbalken
Problemstellung: Ein Auslegerbalken mit der Länge l, der Breite w und der Höhe h. Berechnen Sie die ersten drei Biegemodi und Eigenfrequenzen. (Beachten Sie, dass die Simulationsergebnisse orthogonales Biegen sowie Torsions- und Axialmodi enthalten. Der Ergebnisvergleich vergleicht die ersten drei Biegemodi aus einer Lösung mit geschlossener Form mit den äquivalenten Simulationsergebnissen.)
Quellenangabe: W. T. Thompson, Theory of Vibration with Applications, 2nd Edition, Prentice-Hall, Inc., Englewood Cliffs, NJ, 1981, pg. 220
Materialeigenschaften | Geometrische Eigenschaften |
|---|---|
Elastizitätsmodul E = 70e9 Pa Querkontraktionszahl ν = 0.35 Dichte ⍴ = 2700 kg/m^3 | l= 4 m b = 0.346 m h = 0.346 m |
Ergebnisvergleich – Schieberegler für die Simulationsqualität in der Standardposition
Ergebnisse | Ziel | Creo Simulate | Ansys Discovery Live | Creo Simulation Live | Prozentualer Fehler |
|---|---|---|---|---|---|
Frequenzmodus 1 (Hz) | 17.8 | 17.88 | 17.874 | 17.8 | 0 |
Frequenzmodus 3 (Hz) | 111.5 | 110.03 | 108.22 | 108.16 | 2.99 |
Frequenzmodus 6 (Hz) | 312.1 | 320.22 | 288.37 | 288.58 | 7.54 |
Ergebnisvergleich für Creo Ansys Simulation (Standardnetz)
Ergebnisse | Ziel | Ansys AIM | Creo Ansys Simulation | Prozentualer Fehler |
|---|---|---|---|---|
Frequenzmodus 1 (Hz) | 17.8 | 17.82 | 17.76 | 0.22 |
Frequenzmodus 3 (Hz) | 111.5 | 107.95 | 107.65 | 3.45 |
Frequenzmodus 6 (Hz) | 312.1 | 287.79 | 287.26 | 7.96 |
Modalanalyse für gelenkig gelagerten Balken
Problemstellung: Bestimmung der Grundfrequenz eines gelenkig gelagerten Balkens mit einer Länge von 80 in und eines gleichförmigen Querschnitts A = 4 in2, wie nachfolgend gezeigt.
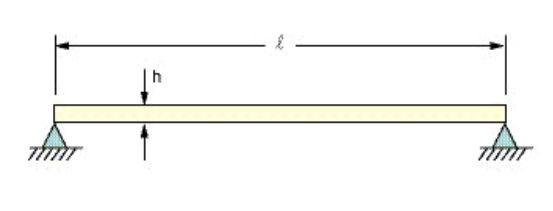
Quellenangabe: W. T. Thompson, Vibration Theory and Applications, 2nd Printing, Prentice-Hall, Inc., Englewood Cliffs, NJ, 1965, pg. 18, ex. 1.5-1
Materialeigenschaften | Geometrische Eigenschaften |
|---|---|
Elastizitätsmodul E = 3e7 psi Querkontraktionszahl ν = 0.3 Dichte ⍴= 0.2836 lb/in^3 | l = 80 in b = 2 in h = 2 in |
Ergebnisvergleich – Schieberegler für die Simulationsqualität in der Standardposition

(Einfache Stützung angenähert durch Hinzufügen einer Randbedingung von 0.125 in aufgeprägten Flächen.)
Ergebnisse | Ziel | Creo Simulate | Ansys Discovery Live | Creo Simulation Live | Prozentualer Fehler |
|---|---|---|---|---|---|
Frequenzmodus 1 (Hz) | 28.766 | 28.67 | 35.089 | 35.5 | 23.4 |
Ergebnisvergleich für Creo Ansys Simulation (Standardnetz)
Ergebnisse | Ziel | Ansys AIM | Creo Ansys Simulation | Prozentualer Fehler |
|---|---|---|---|---|
Frequenzmodus 1 (Hz) | 28.766 | 28.561 | 28.56 | 0.70 |
Modalanalyse für eine ringförmige Platte
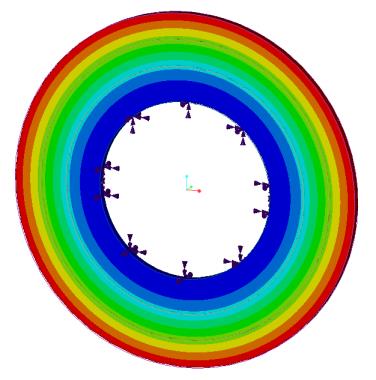
Problemstellung: Für eine Baugruppe mit drei ringförmigen Platten (fest in Radialrichtung, tangentialer und axialer Richtung) wird eine zylinderförmige Stützstruktur auf die zylindrische Fläche der Bohrung angewendet. Bestimmen Sie die ersten sechs Eigenfrequenzen.

Quellenangabe: R. J. Blevins, Formula for Natural Frequency and Mode Shape, Van Nostrand Reinhold Company Inc., 1979, Table 11-2, Case 4, pg. 247
Materialeigenschaften | Geometrische Eigenschaften |
|---|---|
Elastizitätsmodul E = 2.9008e7 psi Querkontraktionszahl ν = 0.3 Dichte ⍴ = 0.28383 lb/in^3 | Innendurchmesser der Innenplatte = 20 in. Innendurchmesser der mittleren Platte = 28 in Innendurchmesser der Außenplatte = 34 in Außendurchmesser der Außenplatte = 40 in Dicke aller Platten = 1 in |
Ergebnisvergleich – Schieberegler für die Simulationsqualität in der Standardposition
Ergebnisse | Ziel | Creo Simulate | Ansys Discovery Live | Creo Simulation Live | Prozentualer Fehler |
|---|---|---|---|---|---|
Frequenzmodus 1 (Hz) | 310.9 | 310.92 | 322.84 | 327.6 | 5.36 |
Frequenzmodus 2 (Hz) | 318.1 | 316.37 | 328.56 | 333.3 | 4.79 |
Frequenzmodus 3 (Hz) | 318.1 | 316.50 | 328.59 | 333.4 | 4.80 |
Frequenzmodus 4 (Hz) | 351.6 | 347.80 | 359.83 | 364.6 | 3.70 |
Frequenzmodus 5 (Hz) | 351.6 | 347.94 | 360.74 | 365.9 | 4.08 |
Frequenzmodus 6 (Hz) | 442.4 | 436.54 | 449.31 | 454.7 | 2.77 |
Ergebnisvergleich für Creo Ansys Simulation (Standard-Netzauflösung)
Ergebnisse | Ziel | Ansys AIM | Creo Ansys Simulation | Prozentualer Fehler |
|---|---|---|---|---|
Frequenzmodus 1 (Hz) | 310.9 | 309.64 | 311.55 | 0.21 |
Frequenzmodus 2 (Hz) | 318.1 | 314.99 | 316.91 | 0.38 |
Frequenzmodus 3 (Hz) | 318.1 | 315 | 317.09 | 0.32 |
Frequenzmodus 4 (Hz) | 351.6 | 345.97 | 348.03 | 1.01 |
Frequenzmodus 5 (Hz) | 351.6 | 345.98 | 349.18 | 0.97 |
Frequenzmodus 6 (Hz) | 442.4 | 434.15 | 436.20 | 1.04 |
Modalanalyse einer rechteckigen Platte
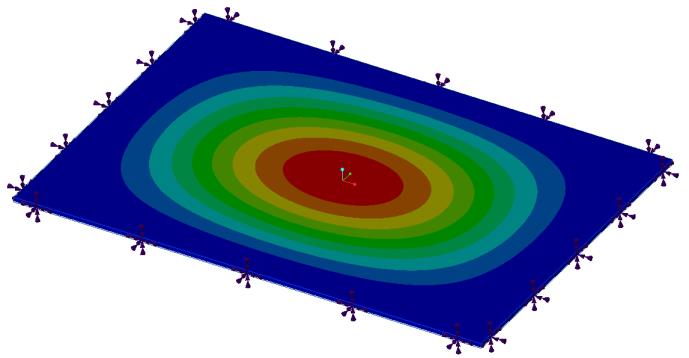
Problemstellung: Eine rechteckige Platte mit festen Stützen, wobei die Bemaßung der Platte wie folgt ist: Länge = 6 in, Breite = 4 in und Dicke = 0.063 in. Bestimmen Sie die Eigenfrequenz und die Eigenmodenform.
Quellenangabe: R. Blevins, Formula for Natural Frequency and Mode Shape, Van Nostrand Reinhold Company Inc., 1979, Table 11-6
Materialeigenschaften | Geometrische Eigenschaften |
|---|---|
Elastizitätsmodul E = 1.0e7 psi Querkontraktionszahl ν = 0.33 Dichte ⍴ = 0.1 lbm/in^3 | Länge = 6 in Breite = 4 in Dicke = 0.063 in |
Ergebnisvergleich – Schieberegler für die Simulationsqualität in der Standardposition
Ergebnisse | Ziel | Creo Simulate | Ansys Discovery Live | Creo Simulation Live | Prozentualer Fehler |
|---|---|---|---|---|---|
Frequenzmodus 1 (Hz) | 1016 | 1019.35 | 1125.2 | 1125.16 | 10.74 |
Ergebnisvergleich für Creo Ansys Simulation (Standard-Netzauflösung)
Ergebnisse | Ziel | Ansys AIM | Creo Ansys Simulation | Prozentualer Fehler |
|---|---|---|---|---|
Frequenzmodus 1 (Hz) | 1016 | 1020.6 | 1024.43 | 0.83 |