Probleme von statischen Analysen
Dieses Kapitel enthält Probleme von statischen Analysen und die Ergebnisse von strukturmechanischen Analysen. In einer statischen Analyse berechnet Creo Simulate Verformungen, Spannungen und Dehnungen in Ihrem Modell, die durch bestimmte Lasten und Randbedingungen entstehen. Creo Simulate berechnet zudem automatisch alle vordefinierten Messgrößen. Diese Liste der Messgrößen variiert je nach dem Analysetyp.
|
|
Beachten Sie, dass Verschiebungswerte immer absolute Werte sind.
|
Dieses Kapitel enthält die folgenden Modelle:
mvss001: 2D Achsensymmetrische zylindrische Schale
|
Analysetyp:
|
Statisch (Static)
|
|
Modelltyp:
|
2D-Achsensymmetrie
|
|
Vergleich:
|
NASTRAN No. V2411
|
|
Hintergrundinformation:
|
• P.E. Grafton und D.R. Strome, "Analysis of Axisymmetrical Shells by the Direct Stiffness Method," AIAA Journal, 1(10): 2342-2347.
• J.W. Jones and H.H. Fong, "Evaluation of NASTRAN," Structural Mechanics Software Series, Vol. IV (N. Perrone and W. Pilkey, eds.), 1982.
|
|
Beschreibung:
|
Bestimmen Sie die radiale Auslenkung am belasteten Ende eines Auslegerzylinders in einem achsensymmetrischen Modell.
|

Element B ist optional. Es sorgt für genauere Ergebnisse im Bereich um das belastete Ende und reduziert die Berechnungszeit. |
Spezifikationen
Art des Elements: | 2D-Schalenelement (2) | |
Einheiten: | IPS | |
Bemaßungen: | Länge: 6 Radius: 5 Dicke: 0.01 | |
Materialeigenschaften: | Massendichte: 0 Massenspezifische Materialkosten: 0 Elastizitätsmodul: 1e7 | Querkontraktionszahl: 0.3 Wärmeausdehnung: 0 Leitfähigkeit: 0 |
Randbedingung: | platziert auf Punkt A: konstant in allen FG | |
Last: | platziert auf Punkt C: FX = 1 Verteilung: Nicht zutreffend Räumliche Verteilung: Nicht zutreffend | |
Vergleich der Ergebnisdaten
Theorie | MSC/NASTRAN | Struktur | % Differenz | |
|---|---|---|---|---|
Radiale Auslenkung @ Last (a=disp_x_radial) | 2.8769e-3 | 2.8715e-3 | 2.8725e-3 | 0.15 % |
Konvergenz %: 0.5 % Lokale Verschiebung und DE | Max P: 7 | Anz. Gleichungen: 33 | ||
mvss002: 2D Achsensymmetrische flache kreisförmige Platte
Analysetyp: | Statisch (Static) |
Modelltyp: | 2D-Achsensymmetrie |
Vergleich: | ANSYS No. 15 |
Hintergrundinformation: | Timoshenko, S. Strength of Materials, Part II, Advanced Theory and Problems. 3. Auflage. NY: D. Van Nostrand Co., Inc. 1956, S. 96, 97 und 103. |
Beschreibung: | Eine flache kreisförmige Platte in einem achsensymmetrischen Modell wird verschiedenen Kantenbedingungen und Flächenbelastungen ausgesetzt. Bestimmen Sie für jeden Fall die maximale Spannung. |

Spezifikationen
Art des Elements: | 2D-Schalenelement (1) | |
Einheiten: | IPS | |
Bemaßungen: | Radius: 40 Dicke: 1 | |
Materialeigenschaften: | Massendichte: 0 Massenspezifische Materialkosten: 0 Elastizitätsmodul: 3e7 | Querkontraktionszahl: 0.3 Wärmeausdehnung: 0 Leitfähigkeit: 0 |
Randbedingungen: | Position | Freiheitsgrade |
|---|---|---|
arretiert | platziert auf Punkt B: | konstant in allen FG |
einfach | platziert auf Punkt B: | konstant in VerschX und VerschY |
Lasten: | Ort/Betrag: | Verteilung: | Räumliche Verteilung: |
|---|---|---|---|
arretiert | platziert auf Kante A-B: FY = 6 | pro Flächeneinheit | gleichmäßig |
einfach | platziert auf Kante A-B: FY = 1.5 | pro Flächeneinheit | gleichmäßig |
Vergleich der Ergebnisdaten
Theorie | ANSYS | Struktur | % Differenz | |
|---|---|---|---|---|
Maximale Spannung (m=max_prin_mag, a=clamped) | 7200 | 7152 | 7200 | 0.0 % |
Konvergenz %: 0.0 % Lokale Verschiebung und DE | Max P: 5 | Anz. Gleichungen: 15 | ||
Maximale Spannung (m=max_prin_mag, a=simple) | 2970 | 2989 | 29701 | 0.0 % |
Konvergenz %: 0.0 % Lokale Verschiebung und DE | Max P: 5 | Anz. Gleichungen: 16 | ||
1 Vorzeichen des Ergebnisses hängt von der Richtung der Last ab.
mvss003: 2D Ebener Spannungszustand Auslegerplatte
Analysetyp: | Statisch (Static) |
Modelltyp: | 2D Ebener Spannungszustand |
Vergleich: | NASTRAN No. V2408A |
Hintergrundinformation: | Singer, Ferdinand L. Strength of Materials. Harper & Row, 1962, Art. 52, S. 133. |
Beschreibung: | Bestimmen Sie die Biegespannung am befestigten Ende einer Auslegerplatte, die einer Schublast in der Ebene ausgesetzt ist. |
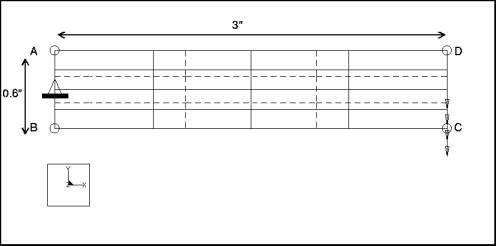
Spezifikationen
Art des Elements: | 2D-Plattenelement (1) | |
Einheiten: | IPS | |
Bemaßungen: | Länge: 3 Höhe: 0.6 Dicke: 0.1 | |
Materialeigenschaften: | Massendichte: 0 Massenspezifische Materialkosten: 0 Elastizitätsmodul: 1.07e7 | Querkontraktionszahl: 0 Wärmeausdehnung: 0 Leitfähigkeit: 0 |
Randbedingungen: | platziert auf Kante A-B: konstant in VerschX, VerschY | |
Lasten: | platziert auf Kante C-D: FY= –200 Verteilung: pro Längeneinheit Räumliche Verteilung: gleichmäßig | |
Die theoretischen Ergebnisse basieren auf der elementaren Balkentheorie. Structure modelliert die tatsächliche physische Struktur. Dabei werden die einzelnen Spannungswerte an den Ecken erfasst, die Bedingungen unterliegen. Wenn Sie die Querkontraktionszahl auf 0 einstellen, liegt das Modell in seiner elementaren Form vor. | ||
Vergleich der Ergebnisdaten
Theorie | MSC/NASTRAN | Struktur | % Differenz | |
|---|---|---|---|---|
Biegespannung @ Knoten A (m=max_stress_xx) | 6.0e4 | 5.5190e4 | 6.0121e4 | 0.20 % |
Konvergenz %: 0.0 % Lokale Verschiebung und DE | Max P: 4 | Anz. Gleichungen: 22 | ||
mvss004: 2D Ebener Dehnungszustand Dickwandiger Zylinder
Analysetyp: | Statisch (Static) |
Modelltyp: | 2D Ebener Dehnungszustand |
Vergleich: | The MacNealHarder Accuracy Tests |
Hintergrundinformation: | MacNeal, R.H., und Harder, R.L. "A Proposed Standard Set of Problems to Test Finite Element Accuracy." Finite Elements in Analysis and Design I. Elsevier Science Publishers, 1985. |
Beschreibung: | Ein dickwandiger Zylinder in einem symmetrischen Modell wird einer internen Druckbelastung ausgesetzt. Bestimmen Sie die radiale Verlagerung am Innenradius für zwei nahezu nicht komprimierbare Materialien. |
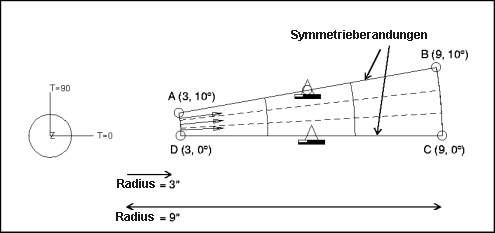
Spezifikationen
Art des Elements: | 2D-Volumenkörper (1) | |
Einheiten: | IPS | |
Bemaßungen: | Außenradius: 9.0 Innenradius: 3.0 | |
Materialeigenschaften: | Massendichte: 0 Massenspezifische Materialkosten: 0 Elastizitätsmodul: 1000 | Querkontraktionszahl: • 0.49 (Fall 1) • 0.499 (Fall 2) |
Randbedingungen (UCS): | platziert auf Kanten A-B & C-D: konstant in allen FG außer TransR | |
Lasten: | platziert auf Kante A-D: Drucklast = 1 Verteilung: Nicht zutreffend Räumliche Verteilung: gleichmäßig | |
Vergleich der Ergebnisdaten
Theorie | Struktur | % Differenz | |
|---|---|---|---|
Radiale Verschiebung @ Innenradius (Fall 1) (m=rad_disp) | 5.0399e-3 | 5.0394e-3 | <0.01 % |
Konvergenz %: 1 % Lokale Verschiebung und DE | Max P: 6 | Anz. Gleichungen: 38 | |
Radiale Verschiebung @ Innenradius (Fall 2) (m=rad_disp) | 5.0602e-3 | 5.0553e-3 | 0.09 % |
Konvergenz %: 1.0 % Lokale Verschiebung und DE | Max P: 6 | Anz. Gleichungen: 38 | |
mvss005: 2D Achsensymmetrischer dickwandiger Zylinder
Analysetyp: | Statisch (Static) |
Modelltyp: | 2D-Achsensymmetrie |
Vergleich: | NASTRAN No. V2410 |
Hintergrundinformation: | Crandall S.H., Dahl N.C., und Larnder T.J. An Introduction to the Mechanics of Solids. 2. Auflage. NY: McGraw-Hill Book Co., 1972, S. 293-297. |
Beschreibung: | Bestimmen Sie die Spannung bei den Radien r = 6.5" und r = 11.5". Ein dickwandiger Zylinder in einem achsensymmetrischen Modell wird einer internen Druckbelastung ausgesetzt. |
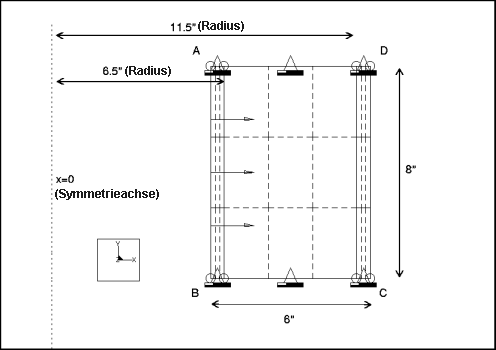
Spezifikationen
Art des Elements: | 2D-Volumenkörper (3) | |
Einheiten: | IPS | |
Bemaßungen: | Innenradius: 6 Höhe: 8 Dicke: 6 | |
Materialeigenschaften: | Massendichte: 0 Massenspezifische Materialkosten: 0 Elastizitätsmodul: 3e7 | Querkontraktionszahl: 0 Wärmeausdehnung: 0 Leitfähigkeit: 0 |
Randbedingungen (UCS): | platziert auf Kanten A-D & B-C: konstant in VerschY und RotZ | |
Lasten: | platziert auf Kante A-B: Drucklast = 10 Verteilung: pro Flächeneinheit Räumliche Verteilung: gleichmäßig | |
Vergleich der Ergebnisdaten
Theorie | MSC/NASTRAN | Struktur | % Differenz | ||
|---|---|---|---|---|---|
@ r = 6.5 | Radialspannung (m=r6_5_radial) | -8.03 | -8.05 | -7.9720 | 0.72 % |
Spannungsbogen (m=r6_5_hoop) | 14.69 | 14.73 | 14.69 | 0.0 % | |
@ r = 11.5 | Radialspannung (m=r11_5_radial) | -0.30 | -0.30 | -2.6636e-1 | 0.0 % |
Spannungsbogen (m=r11_5_hoop) | 6.96 | 6.96 | 6.96 | 0.0 % | |
Konvergenz %: 0.25 % Lokale Verschiebung und DE | Max P: 4 | Anz. Gleichungen: 54 | |||
mvss006: 3D Auslegerbalken
Analysetyp: | Statisch (Static) |
Modelltyp: | 3D |
Vergleich: | NASTRAN No. V2405 |
Hintergrundinformation: | Roark, R.J., und Young, W.C. Formulas for Stress and Strain. NY: McGraw-Hill Book Co., 1982, S. 96. |
Beschreibung: | Ein Auslegerbalken wird an seinem freien Ende einer Last ausgesetzt. Bestimmen Sie die Auslenkung am freien Ende und die Biegespannung am festen Ende. |

Spezifikationen
Art des Elements: | Balken (1) | |
Einheiten: | IPS | |
Bemaßungen: | Länge: 30 | |
Balkeneigenschaften: | Bereich: 0.310 IYY: 0.0241 Schub FY: 10001 CY: 0.5 | J: 0.0631 IZZ: 0.0390 Schub FZ: 10001 CZ: 0.375 |
Materialeigenschaften: | Massendichte: 0 Massenspezifische Materialkosten: 0 Elastizitätsmodul: 1.0e7 | Querkontraktionszahl: 0.3 Wärmeausdehnung: 0 Leitfähigkeit: 0 |
Randbedingungen: | platziert auf Punkt A: konstant in allen FG | |
Lasten: | platziert auf Punkt B: FY = 100 Verteilung: Nicht zutreffend Räumliche Verteilung: Nicht zutreffend | |
1 Strukturbalken berücksichtigen Schub, das dargestellte theoretische Problem hingegen nicht. Dies wird durch die Werte für den Schubfaktor ausgeglichen.
Vergleich der Ergebnisdaten
Theorie | MSC/NASTRAN | Struktur | % Differenz | |
Auslenkung @ Spitze (m=max_disp_y) | 2.3077 | 2.3077 | 2.3094 | 0.073% |
Biegespannung @ Befestigtes Ende(m=max_beam_bending) | 38461 | 38461 | 38461 | 0.0 % |
Konvergenz %: 0.0 % Lokale Verschiebung und DE | Max P: 4 | Anz. Gleichungen: 24 | ||
mvss007: 3D Balken mit mehreren Randbedingungen
Analysetyp: | Statisch (Static) |
Modelltyp: | 3D |
Vergleich: | ANSYS No. 2 |
Hintergrundinformation: | Timoshenko, S. Strength of Materials, Part I, Elementary Theory and Problems. 3. Auflage. NY: D. Van Nostrand Co., Inc., 1955, S. 98, Problem 4. |
Beschreibung: | Ein 30"-WF-Standardbalken, unterstützt wie in der folgenden Abbildung, wird an den Überhängen gleichmäßig belastet. Bestimmen Sie die maximale Biegespannung und Auslenkung in der Mitte des Balkens. |

Spezifikationen
Art des Elements: | Balken (4) | |
Einheiten: | IPS | |
Bemaßungen: | Länge: 480 | |
Balkeneigenschaften: | Bereich: 50.65 IYY: 1 Schub FY: 0.8333 CY: 15 | J: 7893 IZZ: 7892 Schub FZ: 0.8333 CZ: 15 |
Materialeigenschaften: | Massendichte: 0 Massenspezifische Materialkosten: 0 Elastizitätsmodul: 3e7 | Querkontraktionszahl: 0.3 Wärmeausdehnung: 0 Leitfähigkeit: 0 |
Randbedingungen | Position | Freiheitsgrade |
|---|---|---|
platziert auf Punkt B: platziert auf Punkt D: | konstant in allen FG außer RotY und RotZ konstant in VerschY und VerschZ |
Lasten | Ort/Betrag | Verteilung | Räumliche Verteilung |
|---|---|---|---|
platziert auf Kante A-B: FY = 833.33 platziert auf Kante D-E: FY = 833.33 | pro Längeneinheit pro Längeneinheit | gleichmäßig gleichmäßig |
Vergleich der Ergebnisdaten
Theorie | ANSYS | Struktur | % Differenz | |
|---|---|---|---|---|
Max. Biegespannung @ Mitte (m=max_beam_bending) | 11400 | 11404 | 11403.91 | 0.03 % |
Max. Auslenkung @ Mitte (m=disp_center) | 0.182 | 0.182 | 0.182 | 0.0 % |
Konvergenz %: 0.0 % Lokale Verschiebung und DE | Max P: 4 | Anz. Gleichungen: 96 | ||
mvss008: 3D Balken mit parallelogrammförmigen Schalenelementen
Analysetyp: | Statisch (Static) |
Modelltyp: | 3D |
Vergleich: | The MacNealHarder Accuracy Tests |
Hintergrundinformation: | MacNeal, R.H., und Harder, R.L. "A Proposed Standard Set of Problems to Test Finite Element Accuracy." Finite Elements in Analysis and Design I. Elsevier Science Publishers, 1985. |
Beschreibung: | Ein gerader Auslegerbalken, der aus parallelogrammförmigen Elementen zusammengesetzt ist, wird an seinem freien Ende vier verschiedenen Lasten ausgesetzt: • Verlängerung • Schub in der Ebene • Schub außerhalb der Ebene • Verdrehlasten Ermitteln Sie die Verschiebung in Richtung der Last für jeden Fall. |
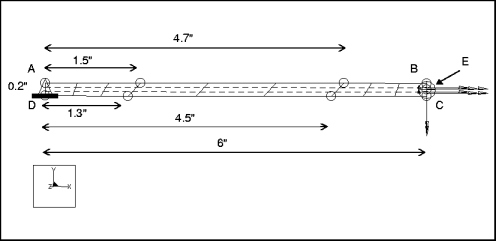
Spezifikationen
Art des Elements: | Schalenelement (3) | |
Einheiten: | IPS | |
Bemaßungen: | Länge: 6 Breite: 0.2 Dicke: 0.1 | |
Materialeigenschaften: | Massendichte: 0 Massenspezifische Materialkosten: 0 Elastizitätsmodul: 1e7 | Querkontraktionszahl: 0.3 Wärmeausdehnung: 0 Leitfähigkeit: 0 |
Randbedingungen: | platziert auf Kante A-D: konstant in allen FG | |
Lasten: | Ort/Betrag: | Verteilung: | Räumliche Verteilung: |
|---|---|---|---|
Verlängerung | platziert auf Kante B-C: FX = 1 | Gesamtlast | gleichmäßig |
in_plane | platziert auf Kante B-C: FY = 1 | Gesamtlast | gleichmäßig |
out_plane | platziert auf Kante B-C: FZ = 1 | Gesamtlast | gleichmäßig |
Verdrehung | platziert auf Punkt E: MX = 1 | Gesamtlast | Nicht zutreffend |
Vergleich der Ergebnisdaten
Theorie | Struktur | % Differenz | |
|---|---|---|---|
Verschiebung der Spitze in Richtung der Last (l=extension, m=max_disp_x) | 3e-5 | 2.998e-5 | 0.06 % |
Verschiebung der Spitze in Richtung der Last (l=in_plane, m=max_disp_y) | 0.1081 | 0.1078 | 0.27 % |
Verschiebung der Spitze in Richtung der Last (l=out_plane, m=max_disp_z) | 0.4321 | 0.4309 | 0.27 % |
Verschiebung der Spitze in Richtung der Last (l=twist, m=max_rot_x) | 0.034081 | 0.03424 | 0.46% |
Konvergenz %: 0.9 % Lokale Verschiebung und DE | Max P: 6 | Anz. Gleichungen: 396 | |
1 In Tabelle 3 (S. 10) der MacNeal-Harder-Referenz für die Verdrehlast an einem geraden Balken liegt ein Druckfehler vor. Der Wert muss 0.03408 lauten.
mvss009: 3D Balken mit trapezoidförmigen Schalenelementen
Analysetyp: | Statisch (Static) |
Modelltyp: | 3D |
Vergleich: | The MacNealHarder Accuracy Tests |
Hintergrundinformation: | MacNeal, R.H., und Harder, R.L. "A Proposed Standard Set of Problems to Test Finite Element Accuracy." Finite Elements in Analysis and Design I. Elsevier Science Publishers, 1985. |
Beschreibung: | Ein gerader Auslegerbalken, der aus trapezoidförmigen Elementen zusammengesetzt ist, wird an seinem freien Ende vier verschiedenen Lasten ausgesetzt: • Verlängerung • Schub in der Ebene • Schub außerhalb der Ebene • verdrehen Ermitteln Sie die Verschiebung in Richtung der Last für jeden Fall. |

Spezifikationen
Art des Elements: | Schalenelement (3) | |
Einheiten: | IPS | |
Bemaßungen: | Länge: 6 Breite: 0.2 Dicke: 0.1 | |
Materialeigenschaften: | Massendichte: 0 Massenspezifische Materialkosten: 0 Elastizitätsmodul: 1e7 | Querkontraktionszahl: 0.3 Wärmeausdehnung: 0 Leitfähigkeit: 0 |
Randbedingungen: | platziert auf Kante A-D: konstant in allen FG | |
Lasten: | Ort/Betrag: | Verteilung: | Räumliche Verteilung: |
|---|---|---|---|
Verlängerung | platziert auf Kante B-C: FX = 1 | Gesamtlast | gleichmäßig |
in_plane | platziert auf Kante B-C: FY = 1 | Gesamtlast | gleichmäßig |
out_plane | platziert auf Kante B-C: FZ = 1 | Gesamtlast | gleichmäßig |
Verdrehung | platziert auf Punkt E: MX = 1 | Gesamtlast | Nicht zutreffend |
Vergleich der Ergebnisdaten
Theorie | Struktur | % Differenz | |
|---|---|---|---|
Verschiebung der Spitze in Richtung der Last (l=extension, m=max_disp_x) | 3e-5 | 2.998e-5 | 0.08 % |
Verschiebung der Spitze in Richtung der Last (l=in_plane, m=max_disp_y) | 0.1081 | 0.1079 | 0.32 % |
Verschiebung der Spitze in Richtung der Last (l=out_plane, m=max_disp_z) | 0.4321 | .4311 | 0.23% |
Verschiebung der Spitze in Richtung der Last (l=twist, m=max_rot_x) | 0.034081 | 0.03381 | 0.79% |
Konvergenz %: 0.7 % Lokale Verschiebung und DE | Max P: 6 | Anz. Gleichungen: 906 | |
1 In Tabelle 3 (S. 10) der MacNeal-Harder-Referenz für die Verdrehlast an einem geraden Balken liegt ein Druckfehler vor. Der Wert muss 0.03408 lauten.
mvss010: 3D Gekrümmter Balken mit Schalen modelliert
Analysetyp: | Statisch (Static) |
Modelltyp: | 3D |
Vergleich: | The MacNealHarder Accuracy Tests |
Hintergrundinformation: | MacNeal, R.H., und Harder, R.L. "A Proposed Standard Set of Problems to Test Finite Element Accuracy." Finite Elements in Analysis and Design I. Elsevier Science Publishers, 1985. |
Beschreibung: | Ein gekrümmter Balken, der einen Bogen von 90  umspannt, ist an einem Ende befestigt und am anderen Ende frei. Bestimmen Sie die Verlagerung der Spitze in Richtung der Last, wenn der Balken am freien Ende einer Last innerhalb und außerhalb der Ebene ausgesetzt wird (2 Fälle). umspannt, ist an einem Ende befestigt und am anderen Ende frei. Bestimmen Sie die Verlagerung der Spitze in Richtung der Last, wenn der Balken am freien Ende einer Last innerhalb und außerhalb der Ebene ausgesetzt wird (2 Fälle). |

Spezifikationen
Art des Elements: | Schalenelement (2) | |
Einheiten: | IPS | |
Bemaßungen: | Außenradius: 4.32 Innenradius: 4.12 Dicke: 0.1 | |
Materialeigenschaften: | Massendichte: 0 Massenspezifische Materialkosten: 0 Elastizitätsmodul: 1e7 | Querkontraktionszahl: 0.25 Wärmeausdehnung: 0 Leitfähigkeit: 0 |
Randbedingungen: | platziert auf Kante A-D: konstant in allen FG | |
Lasten: | Ort/Betrag: | Verteilung: | Räumliche Verteilung: |
|---|---|---|---|
in_plane | platziert auf Kante B-C: FY = 1 | Gesamtlast | gleichmäßig |
out_plane | platziert auf Kante B-C: FZ = 1 | Gesamtlast | gleichmäßig |
Vergleich der Ergebnisdaten
Theorie | Struktur | % Differenz | |
|---|---|---|---|
Verschiebung der Spitze in Richtung der Last (l=in_plane, m=tip_disp_y) | 0.08734 | 0.08833 | 1.13% |
Verschiebung der Spitze in Richtung der Last (l=out_plane, m=tip_disp_z) | 0.5022 | 0.50057 | 0.32 % |
Konvergenz %: 0.3 % Lokale Verschiebung und DE | Max P: 6 | Anz. Gleichungen: 234 | |
mvss011: 3D Gelenkig gelagerte rechteckige Platte
Analysetyp: | Statisch (Static) |
Modelltyp: | 3D |
Vergleich: | The MacNealHarder Accuracy Tests |
Hintergrundinformation: | MacNeal, R.H., und Harder, R.L. "A Proposed Standard Set of Problems to Test Finite Element Accuracy." Finite Elements in Analysis and Design I. Elsevier Science Publishers, 1985. |
Beschreibung: | Eine flache Platte wird an allen vier Kanten gelenkig gelagert. Ein Viertel der Platte ist symmetrisch modelliert. Die Platte wird durch gleichmäßigen Druck und eine Punktlast im Zentrum zwei verschiedenen Lasten ausgesetzt. Ermitteln Sie die Verschiebung im Mittelpunkt der Platte. |
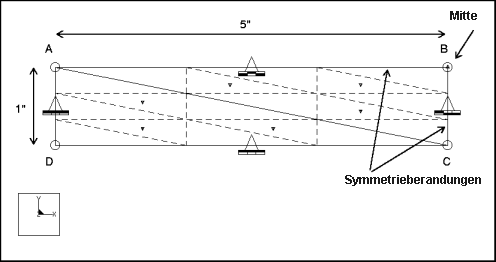
Spezifikationen
Art des Elements: | Schalenelement (2) | |
Einheiten: | IPS | |
Bemaßungen: | Länge: 5 Breite: 1 Dicke: 0.0001 | |
Materialeigenschaften: | Massendichte: 0 Massenspezifische Materialkosten: 0 Elastizitätsmodul: 1.7472e7 | Querkontraktionszahl: 0.3 Wärmeausdehnung: 0 Leitfähigkeit: 0 |
Randbedingungen | Position | Freiheitsgrade |
|---|---|---|
platziert auf Kanten A-D, C-D: platziert auf Kante A-B: platziert auf Kante B-C: | konstant in VerschX, VerschY und VerschZ konstant in VerschY, RotX und RotZ konstant in VerschX, RotY und RotZ |
Lasten: | Ort/Betrag: | Verteilung: | Räumliche Verteilung: |
|---|---|---|---|
Druck | platziert auf allen Schalen: Druck = 1e4 | Gesamtlast pro Flächeneinheit | gleichmäßig |
Punkt | platziert auf Punkt B: FZ = 1e4 | Nicht zutreffend | Nicht zutreffend |
Vergleich der Ergebnisdaten
Theorie | Struktur | % Differenz | |
|---|---|---|---|
Verschiebung @ Mittelpunkt (l=pressure, m=disp_z_cen) | 12.97 | 12.97 | 0.0 % |
Verschiebung @ Mittelpunkt (l=point, m=disp_z_cen) | 16.96 | 16.81 | 0.88% |
Konvergenz %: 0.8 % Lokale Verschiebung und DE | Max P: 9 | Anz. Gleichungen: 438 | |
mvss012: 3D Arretierte rechteckige Platte
Analysetyp: | Statisch (Static) |
Modelltyp: | 3D |
Vergleich: | The MacNealHarder Accuracy Tests |
Hintergrundinformation: | MacNeal, R.H., und Harder, R.L. "A Proposed Standard Set of Problems to Test Finite Element Accuracy." Finite Elements in Analysis and Design I. Elsevier Science Publishers, 1985. |
Beschreibung: | Ein Viertel einer an vier Kanten arretierten rechteckigen Platte ist symmetrisch modelliert. Die Platte wird durch gleichmäßigen Druck und eine Punktlast im Zentrum zwei verschiedenen Lasten ausgesetzt. Ermitteln Sie die Verschiebung im Mittelpunkt der Platte. |

Spezifikationen
Art des Elements: | Schalenelement (2) | |
Einheiten: | IPS | |
Bemaßungen: | Länge: 5 Breite: 1 Dicke: 0.0001 | |
Materialeigenschaften: | Massendichte: 0 Massenspezifische Materialkosten: 0 Elastizitätsmodul: 1.7472e7 | Querkontraktionszahl: 0.3 Wärmeausdehnung: 0 Leitfähigkeit: 0 |
Randbedingungen | Position | Freiheitsgrade |
|---|---|---|
platziert auf Kanten A-D, D-C: platziert auf Kante A-B: platziert auf Kante B-C: | konstant in allen FG konstant in VerschY, RotX und RotZ konstant in VerschX, RotY und RotZ |
Lasten: | Ort/Betrag: | Verteilung: | Räumliche Verteilung: |
|---|---|---|---|
Druck | platziert auf allen Schalen: Druck = 1e4 | pro Flächeneinheit | gleichmäßig |
Punkt | platziert auf Punkt B: FZ = 1e4 | Nicht zutreffend | Nicht zutreffend |
Vergleich der Ergebnisdaten
Theorie | Struktur | % Differenz | |
|---|---|---|---|
Verschiebung @ Mittelpunkt (l=pressure, m=measure1) | 2.56 | 2.604 | 1.71 % |
Verschiebung @ Mittelpunkt (l=point, m=measure1) | 7.23 | 7.168 | 0.85% |
Konvergenz %: 1.3 % Lokale Verschiebung und DE | Max P: 9 | Anz. Gleichungen: 625 | |
mvss013: 3D Halbkugelförmige Schale
Analysetyp: | Statisch (Static) |
Modelltyp: | 3D |
Vergleich: | The MacNealHarder Accuracy Tests |
Hintergrundinformation: | MacNeal, R.H., und Harder, R.L. "A Proposed Standard Set of Problems to Test Finite Element Accuracy." Finite Elements in Analysis and Design I. Elsevier Science Publishers, 1985. |
Beschreibung: | Ein Viertel einer offenen Halbkugel ist symmetrisch modelliert und wird am Äquator im Abstand von 90  mit wechselnden Punktlasten belastet. Bestimmen Sie die radiale Verlagerung an jedem Ansatzpunkt der Last. mit wechselnden Punktlasten belastet. Bestimmen Sie die radiale Verlagerung an jedem Ansatzpunkt der Last. |

Spezifikationen
Art des Elements: | Schalenelement (4) | |
Einheiten: | IPS | |
Bemaßungen: (mit Hilfe eines Viertelmodells) | Radius: 10 Bogen: 90o Dicke: 0.04 | |
Materialeigenschaften: | Massendichte: 0 Massenspezifische Materialkosten: 0 Elastizitätsmodul: 6.825e7 | Querkontraktionszahl: 0.3 Wärmeausdehnung: 0 Leitfähigkeit: 0 |
Randbedingungen | Position | Freiheitsgrade |
|---|---|---|
platziert auf Kurve A-C: platziert auf Kurve G-E: platziert auf Punkt D | konstant in VerschP, RotR und RotT konstant in VerschP, RotR und RotT konstant in VerschT |
Lasten: | Ort/Betrag: | Verteilung: | Räumliche Verteilung |
|---|---|---|---|
platziert auf Punkt C: FR = 1 platziert auf Punkt E: FR = 1 | Nicht zutreffend Nicht zutreffend | Nicht zutreffend Nicht zutreffend |
Vergleich der Ergebnisdaten
Theorie | Struktur | % Differenz | |
|---|---|---|---|
Radiale Verlagerung @ Last (m=disp_rad) | 0.0924 | 0.0933 | 0.97 % |
Konvergenz %: 0.6 % Lokale Verschiebung und DE | Max P: 9 | Anz. Gleichungen: 1965 | |
mvss014: 3D-Auslegerbalken verdreht um 90

Analysetyp: | Statisch (Static) |
Modelltyp: | 3D |
Vergleich: | The MacNealHarder Accuracy Tests |
Hintergrundinformation: | MacNeal, R.H., und Harder, R.L. "A Proposed Standard Set of Problems to Test Finite Element Accuracy." Finite Elements in Analysis and Design I. Elsevier Science Publishers, 1985. |
Beschreibung: | Ein um 90  verdrehter Auslegerbalken wird an seinem freien Ende Lasten innerhalb und außerhalb der Ebene ausgesetzt. Ermitteln Sie die Verschiebung in Richtung der Last für jeden Fall. verdrehter Auslegerbalken wird an seinem freien Ende Lasten innerhalb und außerhalb der Ebene ausgesetzt. Ermitteln Sie die Verschiebung in Richtung der Last für jeden Fall. |

Spezifikationen
Art des Elements: | Volumenkörper (2) | |
Einheiten: | IPS | |
Bemaßungen: | Länge: 12 Breite: 1.1 Dicke: 0.32 Verdrehungswinkel 90o (vom festen zum freien Ende) | |
Materialeigenschaften: | Massendichte: 0 Massenspezifische Materialkosten: 0 Elastizitätsmodul: 29e6 | Querkontraktionszahl: 0.22 Wärmeausdehnung: 0 Leitfähigkeit: 0 |
Randbedingungen: | platziert auf ursprünglicher Fläche: konstant in allen FG | |
Lasten: | Ort/Betrag: | Verteilung: | Räumliche Verteilung: |
|---|---|---|---|
in_plane | platziert auf freier Endfläche: FY = 1 | Gesamtlast | gleichmäßig |
out_plane | platziert auf freier Endfläche: FZ = 1 | Gesamtlast | gleichmäßig |
Vergleich der Ergebnisdaten
Theorie | Struktur | % Differenz | |
|---|---|---|---|
Verschiebung der Spitze in Richtung der Last (l=in_plane, m=disp_tip_y1) | 0.005424 | 0.005428 | 0.73% |
Verschiebung der Spitze in Richtung der Last (l=out_of_plane, m=disp_tip_z1) | 0.001754 | 0.001760 | 0.342% |
Konvergenz %: 0.8 % Lokale Verschiebung und DE | Max P: 5 | Anz. Gleichungen: 590 | |
mvss015: 3D Scordelis-Lo-Dach
Analysetyp: | Statisch (Static) |
Modelltyp: | 3D |
Vergleich: | The MacNealHarder Accuracy Tests |
Hintergrundinformation: | MacNeal, R.H., und Harder, R.L. "A Proposed Standard Set of Problems to Test Finite Element Accuracy." Finite Elements in Analysis and Design I. Elsevier Science Publishers, 1985. |
Beschreibung: | Ein Scordelis-Lo-Dach bildet ein Viertel eines gewölbten Daches, das symmetrisch modelliert ist und gleichmäßig belastet wird. Bestimmen Sie die vertikale Verlagerung am Mittelpunkt der geraden Seite (des gesamten Daches). |

Spezifikationen
Art des Elements: | Schalenelement (1) | |
Einheiten: | IPS | |
Bemaßungen: (mit Hilfe eines Viertelmodells) | Länge: 25 Radius: 25 Bogen: 40o Dicke: 0.25 | |
Materialeigenschaften: | Massendichte: 0 Massenspezifische Materialkosten: 0 Elastizitätsmodul: 4.32e8 | Querkontraktionszahl: 0 Wärmeausdehnung: 0 Leitfähigkeit: 0 |
Randbedingungen | Position | Freiheitsgrade |
|---|---|---|
(UCS) (UCS) (UCS) | platziert auf Kurve A-B: platziert auf Kurve A-D: platziert auf Kurve C-D | konstant in VerschZ, RotR und RotT konstant in VerschT, RotZ und RotR konstant in VerschR und VerschT |
Lasten: | Ort/Betrag: | Verteilung: | Räumliche Verteilung: |
|---|---|---|---|
platziert auf Fläche A-B-C-D: FZ = 90 | pro Flächeneinheit | gleichmäßig |
Vergleich der Ergebnisdaten
Theorie | Struktur | % Differenz | |
|---|---|---|---|
Vertikale Verlagerung @ Punkt B (m=disp_z_mid) | 0.3024 | 0.3008 | 0.53 % |
Konvergenz %: 0.2 % Lokale Verschiebung und DE | Max P: 7 | Anz. Gleichungen: 148 | |
mvss016: 2D Achsensymmetrischer Zylinder/Kugel
Analysetyp: | Statisch (Static) |
Modelltyp: | 2D-Achsensymmetrie |
Hintergrundinformation: | NAFEMS, LSB1, Nr. IC 39 |
Beschreibung: | Ein achsensymmetrischer Zylinder und ein halbkugelförmiger Behälter werden einem gleichmäßigen internen Druck ausgesetzt. Bestimmen Sie die Gebindespannung an der Außenfläche bei Punkt D. |

Spezifikationen
Art des Elements: | 2D-Schalenelement (4) | |
Einheiten: | MKS | |
Bemaßungen: | Radius: 1 Dicke: 0.025 | |
Materialeigenschaften: | Massendichte: 0.007 Massenspezifische Materialkosten: 0 Elastizitätsmodul: 210000 | Querkontraktionszahl: 0.3 Wärmeausdehnung: 0 Leitfähigkeit: 0 |
Randbedingungen | Position | Freiheitsgrade |
|---|---|---|
constraint1 | platziert auf Punkt A: platziert auf Punkt E: | konstant in VerschX und RotZ konstant in VerschY |
Lasten: | Ort/Betrag: | ||
|---|---|---|---|
load1 | platziert auf allen 2D-Schalenelementen: interner Druck = 1 | ||
Vergleich der Ergebnisdaten
Theorie | Struktur1 | % Differenz | |
|---|---|---|---|
Szz auf Außenfläche | 38.5 | 38.62 | 0.3 % |
Konvergenz %: 0.8 % Lokale Verschiebung und DE | Max P: 7 | Anz. Gleichungen: 72 | |
1 Sie können die Ergebnisse im Statusbericht nicht anzeigen. Definieren Sie stattdessen ein Ergebnisfenster für die Spannung ZZ (unten), und fragen Sie den Wert an Punkt D ab.
mvss017: 2D Konische Membran mit Gravitationslast
Analysetyp: | Statisch (Static) |
Modelltyp: | Ebener Spannungszustand |
Hintergrundinformation: | NAFEMS, LSB1, Nr. IC 2 |
Beschreibung: | Eine konische Membran ist einer gleichmäßigen Beschleunigung in globaler X-Richtung ausgesetzt. Bestimmen Sie die direkte Spannung Sxx an Punkt B. |

Spezifikationen
Art des Elements: | 2D-Plattenelement (2) | |
Einheiten: | MKS | |
Bemaßungen: | Dicke: 0.1 | |
Materialeigenschaften: | Massendichte: 0.007 Massenspezifische Materialkosten: 0 Elastizitätsmodul: 210000 | Querkontraktionszahl: 0.3 Wärmeausdehnung: 0 Leitfähigkeit: 0 |
Randbedingungen: | Position | Freiheitsgrade |
|---|---|---|
constraint1 | platziert auf Kurven A-B, B-C: platziert auf Punkt B: | konstant in VerschX konstant in VerschX, VerschY |
Lasten: | Ort/Betrag: |
|---|---|
load1 | Globale Beschleunigung: GX = 9.81 |
Vergleich der Ergebnisdaten
Theorie | Struktur | % Differenz | |
|---|---|---|---|
Spannung XX an Punkt B (m=measure1) | 0.247 | 0.247 | 0 % |
Konvergenz %: 0.7 % Lokale Verschiebung und DE | Max P: 7 | Anz. Gleichungen: 248 | |
mvss018: 3D Z-Schnitt Auslegerplatte
Analysetyp: | Statisch (Static) |
Modelltyp: | 3D |
Hintergrundinformation: | NAFEMS, LSB1, Nr. IC 29 |
Beschreibung: | Eine Auslegerplatte im Z-Schnitt wird an ihrem freien Ende durch zwei gleichmäßig verteilte Kantenschübe einem Drehmoment ausgesetzt. Bestimmen Sie die direkte Spannung Sxx in der Mittenebene der Platte. |
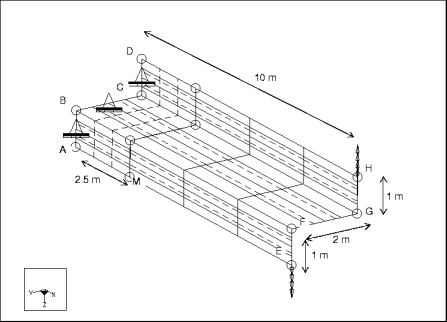
Spezifikationen
Art des Elements: | Schalenelement (6) | |
Einheiten: | MKS | |
Bemaßungen: | Länge: 10 Dicke: 0.1 | |
Materialeigenschaften: | Massendichte: 0.007 Massenspezifische Materialkosten: 0 Elastizitätsmodul: 210000 | Querkontraktionszahl: 0.3 Wärmeausdehnung: 0 Leitfähigkeit: 0 |
Randbedingungen | Position | Freiheitsgrade |
|---|---|---|
constraint1 | platziert auf Kurven A-B, B-C und C-D: | konstant in VerschX, VerschY und VerschZ |
Lasten: | Ort/Betrag: | Verteilung | Räumliche Verteilung |
|---|---|---|---|
load1 | platziert auf Kurve E-F: FZ=0.6 platziert auf Kurve G-H: FZ=0.6 | Gesamtlast Gesamtlast | gleichmäßig gleichmäßig |
Vergleich der Ergebnisdaten
Theorie | Struktur1 | % Differenz | |
|---|---|---|---|
Sxx in Mittenebene an Punkt M | 108.8 | 110.02 | 1.1 % |
Konvergenz %: 0.4 % Lokale Verschiebung und DE | Max P: 7 | Anz. Gleichungen: 870 | |
1 Sie können die Ergebnisse im Statusbericht nicht anzeigen. Definieren Sie stattdessen ein Ergebnisfenster für die Spannung XX (oben und unten), und fragen Sie den Wert an Punkt M ab. Bilden Sie dann den Durchschnitt der Werte für oben (118) und unten (105.56).
mvss019: 3D Zylindrische Schale mit Kantenmoment
Analysetyp: | Statisch (Static) |
Modelltyp: | 3D |
Hintergrundinformation: | NAFEMS, LSB1, Nr. IC 19 |
Beschreibung: | Eine zylindrische Schale im 3D-Raum wird an einer Kante mit einem gleichmäßigen normalen Kantenmoment belastet. Ermitteln Sie die tangentiale Spannung der Außenfläche an Punkt E. |
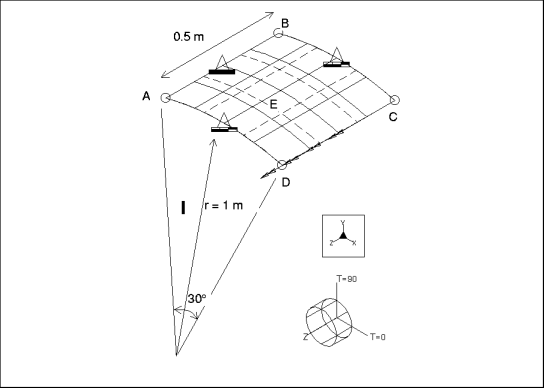
Spezifikationen
Art des Elements: | Schalenelement (1) | |
Einheiten: | MKS | |
Bemaßungen: | Radius: 1 Dicke: 0.01 | |
Materialeigenschaften: | Massendichte: 0.007 Massenspezifische Materialkosten: 0 Elastizitätsmodul: 210000 | Querkontraktionszahl: 0.3 Wärmeausdehnung: 0 Leitfähigkeit: 0 |
Randbedingungen | Position | Freiheitsgrade |
|---|---|---|
constraint1 | platziert auf Kurve A-B: platziert auf Kurven A-D und B-C: | konstant in allen FG konstant in VerschZ, RotX und RotY |
Lasten: | Ort/Betrag: | Verteilung | Räumliche Verteilung |
|---|---|---|---|
load1 | platziert auf Kurve C-D: MZ=0.001 | Kraft pro Längeneinheit | gleichmäßig |
Vergleich der Ergebnisdaten
Theorie | Struktur1 | % Differenz | |
|---|---|---|---|
Sxx auf Außenfläche an Punkt E | 60.0 | 59.6 | .67 % |
Konvergenz %: 0.9 % Lokale Verschiebung und DE | Max P: 5 | Anz. Gleichungen: 66 | |
1 Sie können die Ergebnisse im Statusbericht nicht anzeigen. Definieren Sie stattdessen ein Ergebnisfenster mit Flächenraster für die Spannung XX (oben), und fragen Sie den Wert an Punkt E ab.
mvss020: Balkenquerschnitte
Analysetyp: | Statisch (Static) |
Modelltyp: | 3D |
Vergleich: | Theorie |
Hintergrundinformation: | Roark, R.J., und Young, W.C. Formulas for Stress and Strain. 5. Auflage. NY: McGraw Hill Book Co. 1982, S. 64. |
Beschreibung: | Ein Auslegerbalken wird transversalen Lasten in Y- und Z-Richtung und einer axialen Last in X-Richtung ausgesetzt. Bestimmen Sie die Auslenkung am freien Ende, die Biegespannung am festen Ende und die axiale Spannung entlang des Balkens. |
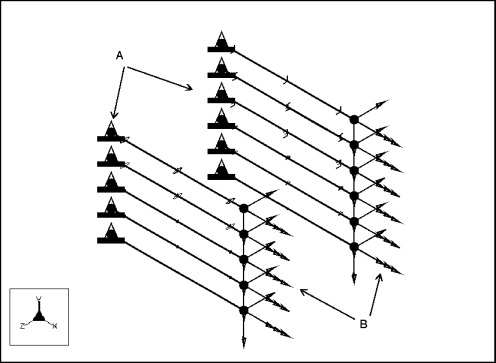
Dieses Balkenprofilmodell verwendet die folgenden Elementtypen und Ergebnisse:
In allen Fällen hängt die Verlagerung von der Richtung der Last ab. Die Ergebnisse unter Auslenkung an der Spitze können bei diesem Problem daher sowohl positiv als auch negativ sein. |
Quadratischer Balken
Spezifikationen
Art des Elements: | Quadratischer Balken | |
Einheiten: | IPS | |
Bemaßungen: | a: 0.25 | |
Balkeneigenschaften: | Bereich: 0.0625 IYY: 0.000325521 Schub FY: 10001 CY: 0.125 | J: 0.000549316 IZZ: 0.000325521 Schub FZ: 10001 CZ: 0.125 |
Materialeigenschaften: | Massendichte: 0 Massenspezifische Materialkosten: 0 Elastizitätsmodul: 3e7 | Querkontraktionszahl: 0.3 Wärmeausdehnung: 0 Leitfähigkeit: 0 |
Randbedingungen: | platziert auf Punkt A: konstant in allen FG | |
Last: | Position: | Betrag: |
axial | platziert auf Punkt B | FX=100 |
quer y | platziert auf Punkt B | FY=100 |
quer z | platziert auf Punkt B | FZ=100 |
1 Strukturbalken berücksichtigen Schub, das dargestellte theoretische Problem hingegen nicht. Dies wird durch die Werte für den Schubfaktor ausgeglichen.
Vergleich der Ergebnisdaten (Quadratischer Balken)
Last | Messgröße | Theorie | Struktur | % Differenz |
|---|---|---|---|---|
Auslenkung an der Spitze: | ||||
axial | sq_d_x | 1.6e-3 | 1.6e-3 | 0 % |
quer y | sq_d_y | 9.216e1 | 9.216e1 | 0 % |
quer z | sq_d_z | 9.216e1 | 9.216e1 | 0 % |
Spannung: | ||||
axial | sq_s_ten | 1.6e3 | 1.6e3 | 0 % |
quer y | sq_s_bnd | 1.152003e6 | 1.15200e6 | 0 % |
quer z | sq_s_bnd | 1.152003e6 | 1.15200e6 | 0 % |
Last | Lkle Versch & DE | Max P | Anz. Gleichungen | |
|---|---|---|---|---|
Konvergenz: | ||||
axial | 0 % | 2 | 264 | |
quer y | 0 % | 2 | 264 | |
quer z | 0 % | 2 | 264 | |
Rechteckiger Balken
Spezifikationen
Art des Elements: | Rechteckiger Balken | |
Einheiten: | IPS | |
Bemaßungen: | b: 1 d: 0.25 | |
Balkeneigenschaften: | Bereich: 0.25 IYY: 0.0208333 Schub FY: 10001 CY: 0.125 | J: 0.00438829 IZZ: 0.00130208 Schub FZ: 10001 CZ: 0.5 |
Materialeigenschaften: | Massendichte: 0 Massenspezifische Materialkosten: 0 Elastizitätsmodul: 3e7 | Querkontraktionszahl: 0.3 Wärmeausdehnung: 0 Leitfähigkeit: 0 |
Randbedingungen: | platziert auf Punkt A: konstant in allen FG | |
Last: | Position: | Betrag: |
axial | platziert auf Punkt B | FX=100 |
quer y | platziert auf Punkt B | FY=100 |
quer z | platziert auf Punkt B | FZ=100 |
1 Strukturbalken berücksichtigen Schub, das dargestellte theoretische Problem hingegen nicht. Dies wird durch die Werte für den Schubfaktor ausgeglichen.
Vergleich der Ergebnisdaten (Rechteckiger Balken)
Last | Messgröße | Theorie | Struktur | % Differenz |
|---|---|---|---|---|
Auslenkung an der Spitze: | ||||
axial | rct_d_x | 4.0e-4 | 4.0e-4 | 0 % |
quer y | rct_d_y | 2.304e1 | 2.304e1 | 0 % |
quer z | rct_d_z | 1.44 | 1.44 | 0 % |
Spannung: | ||||
Last | Messgröße | Theorie | Struktur | % Differenz |
axial | rct_s_ten | 4.0e2 | 4.0e2 | 0 % |
quer y | rct_s_bnd | 2.880e5 | 2.880e5 | 0 % |
quer z | rct_s_bnd | 7.200e4 | 7.200e4 | 0 % |
Last | Lkle Versch & DE | Max P | Anz. Gleichungen | |
|---|---|---|---|---|
Konvergenz: | ||||
axial | 0 % | 2 | 264 | |
quer y | 0 % | 2 | 264 | |
quer z | 0 % | 2 | 264 | |
Hohler rechteckiger Balken
Spezifikationen
Art des Elements: | Hohler rechteckiger Balken | |
Einheiten: | IPS | |
Bemaßungen: | b: 1 bi: 0.875 d: 0.25 di: 0.125 | |
Balkeneigenschaften: | Bereich: 0.140625 IYY: 0.013855 Schub FY: 10001 CY: 0.125 | J: 0.00343323 IZZ: 0.00115967 Schub FZ: 10001 CZ: 0.5 |
Materialeigenschaften: | Massendichte: 0 Massenspezifische Materialkosten: 0 Elastizitätsmodul: 3e7 | Querkontraktionszahl: 0.3 Wärmeausdehnung: 0 Leitfähigkeit: 0 |
Randbedingungen: | platziert auf Punkt A: konstant in allen FG | |
Last: | Position: | Betrag: |
axial | platziert auf Punkt B | FX=100 |
quer y | platziert auf Punkt B | FY=100 |
quer z | platziert auf Punkt B | FZ=100 |
1 Strukturbalken berücksichtigen Schub, das dargestellte theoretische Problem hingegen nicht. Dies wird durch die Werte für den Schubfaktor ausgeglichen.
Vergleich der Ergebnisdaten (Hohler rechteckiger Balken)
Last | Messgröße | Theorie | Struktur | % Differenz |
|---|---|---|---|---|
Auslenkung an der Spitze: | ||||
axial | hrct_d_x | 7.112e-4 | 7.111e-4 | 0.02 % |
quer y | hrct_d_y | 2.5869e1 | 2.5876e1 | 0.027% |
quer z | hrct_d_z | 2.1653 | 2.1677 | 0.10% |
Spannung: | ||||
Last | Messgröße | Theorie | Struktur | % Differenz |
axial | hrct_s_ten | 7.112e2 | 7.111e2 | 0.01% |
quer y | hrct_s_bnd | 3.2337e5 | 3.2336e5 | 0.003% |
quer z | hrct_s_bnd | 1.0826e5 | 1.0826e5 | 0 % |
Last | Lkle Versch & DE | Max P | Anz. Gleichungen | |
|---|---|---|---|---|
Konvergenz: | ||||
axial | 0 % | 2 | 264 | |
quer y | 0 % | 2 | 264 | |
quer z | 0 % | 2 | 264 | |
U-Balken
Spezifikationen
Art des Elements: | U-Balken | |
Einheiten: | IPS | |
Bemaßungen: | b: 1 di: 1 t: 0.125 tw: 0.125 | |
Balkeneigenschaften: | Bereich: 0.375 IYY: 0.0369466 Schub FY: 10001 CY: 0.625 | J: 0.00179932 IZZ: 0.0898438 Schub FZ: 10001 CZ: 0.645833 |
Materialeigenschaften: | Massendichte: 0 Massenspezifische Materialkosten: 0 Elastizitätsmodul: 3e7 | Querkontraktionszahl: 0.3 Wärmeausdehnung: 0 Leitfähigkeit: 0 |
Randbedingungen: | platziert auf Punkt A: konstant in allen FG | |
Last: | Position: | Betrag: |
axial | platziert auf Punkt B | FX=100 |
quer y | platziert auf Punkt B | FY=100 |
quer z | platziert auf Punkt B | FZ=100 |
1 Strukturbalken berücksichtigen Schub, das dargestellte theoretische Problem hingegen nicht. Dies wird durch die Werte für den Schubfaktor ausgeglichen.
Vergleich der Ergebnisdaten (U-Balken)
Last | Messgröße | Theorie | Struktur | % Differenz |
|---|---|---|---|---|
Auslenkung an der Spitze: | ||||
axial | chnl_d_x | 2.6667e-4 | 2.666667e-04 | 0 % |
quer y | chnl_d_y | 3.339e-1 | 4.004507e-01 | 19.93 % |
quer z | chnl_d_z | 8.1198e-1 | 8.1198e-1 | 0 % |
Spannung: | ||||
Last | Messgröße | Theorie | Struktur | % Differenz |
axial | chnl_s_ten | 2.6667e2 | 2.6667e2 | 0 % |
quer y | chnl_s_bnd | 2.087e4 | 2.087e4 | 0 % |
quer z | chnl_s_bnd | 5.244e4 | 5.244e4 | 0 % |
Konvergenz: | ||||
Last | Lkle Versch & DE | Max P | Anz. Gleichungen | |
axial | 0 % | 4 | 264 | |
quer y | 0 % | 4 | 264 | |
quer z | 0 % | 4 | 264 | |
I-Balken
Spezifikationen
Art des Elements: | I-Balken | |
Einheiten: | IPS | |
Bemaßungen: | b: 1 di: 1 t: 0.125 tw: 0.125 | |
Balkeneigenschaften: | Bereich: 0.375 IYY: 0.0209961 Schub FY: 10001 CY: 0.625 | J: 0.00179932 IZZ: 0.0898438 Schub FZ: 10001 CZ: 0.5 |
Materialeigenschaften: | Massendichte: 0 Massenspezifische Materialkosten: 0 Elastizitätsmodul: 3e7 | Querkontraktionszahl: 0.3 Wärmeausdehnung: 0 Leitfähigkeit: 0 |
Randbedingungen: | platziert auf Punkt A: konstant in allen FG | |
Last: | Position: | Betrag: |
axial | platziert auf Punkt B | FX=100 |
quer y | platziert auf Punkt B | FY=100 |
quer z | platziert auf Punkt B | FZ=100 |
1 Strukturbalken berücksichtigen Schub, das dargestellte theoretische Problem hingegen nicht. Dies wird durch die Werte für den Schubfaktor ausgeglichen.
Vergleich der Ergebnisdaten (I-Balken)
Last | Messgröße | Theorie | Struktur | % Differenz |
|---|---|---|---|---|
Auslenkung an der Spitze: | ||||
axial | I_d_x | 2.6667e-4 | 2.6667e-4 | 0 % |
quer y | I_d_y | 3.3391e-1 | 3.3573e-1 | 0.54% |
quer z | I_d_z | 1.4288 | 1.4296 | 0.05 % |
Spannung: | ||||
Last | Messgröße | Theorie | Struktur | % Differenz |
axial | I_s_ten | 2.6667e2 | 2.6667e2 | 0 % |
quer y | I_s_bnd | 2.0870e4 | 2.0869e4 | 0.004 % |
quer z | I_s_bnd | 7.1442e4 | 7.14418e4 | 0.001% |
Last | Lkle Versch & DE | Max P | Anz. Gleichungen | |
|---|---|---|---|---|
Konvergenz: | ||||
axial | 0 % | 2 | 264 | |
quer y | 0 % | 2 | 264 | |
quer z | 0 % | 2 | 264 | |
L-Balken
Spezifikationen
Art des Elements: | L-Balken | |
Einheiten: | IPS | |
Bemaßungen: | b: 1 d: 1 t: 0.125 tw: 0.125 | |
Balkeneigenschaften: | Bereich: 0.25 IYY: 0.0105794 Schub FY: 10001 CY: 0.789352 | J: 0.00119955 IZZ: 0.0423177 Schub FZ: 10001 CZ: 0.433047 |
Materialeigenschaften: | Massendichte: 0 Massenspezifische Materialkosten: 0 Elastizitätsmodul: 3e7 | Querkontraktionszahl: 0.3 Wärmeausdehnung: 0 Leitfähigkeit: 0 |
Randbedingungen: | platziert auf Punkt A: konstant in allen FG | |
Last: | Position: | Betrag: |
axial | platziert auf Punkt B | FX=100 |
quer y | platziert auf Punkt B | FY=100 |
quer z | platziert auf Punkt B | FZ=100 |
1 Strukturbalken berücksichtigen Schub, das dargestellte theoretische Problem hingegen nicht. Dies wird durch die Werte für den Schubfaktor ausgeglichen.
Vergleich der Ergebnisdaten (L-Balken)
Last | Messgröße | Theorie | Struktur | % Differenz |
|---|---|---|---|---|
Auslenkung an der Spitze: | ||||
axial | L_d_x | 4.0e-4 | 4.0e-4 | 0 % |
quer y | L_d_y | 7.0892e-1 | 7.089233e-01 | 0.0004 % |
quer z | L_d_z | 2.8357 | 2.835700 | 0 % |
Spannung: | ||||
Last | Messgröße | Theorie | Struktur | % Differenz |
axial | L_s_ten | 4e2 | 4e2 | 0 % |
quer y | L_s_ben | 5.5611e4 | 5.595900e+04 | 0.62 % |
quer z | L_s_ben | 1.228e5 | 1.227991e+05 | 0.0007 % |
Last | Lkle Versch & DE | Max P | Anz. Gleichungen | |
|---|---|---|---|---|
Konvergenz: | ||||
axial | 0 % | 2 | 264 | |
quer y | 0 % | 2 | 264 | |
quer z | 0 % | 2 | 264 | |
Rhombusförmiger Balken
Spezifikationen
Art des Elements: | Rhombusförmiger Balken | |
Einheiten: | IPS | |
Bemaßungen: | b: 0.25 d: 0.25 | |
Balkeneigenschaften: | Bereich: 0.03125 IYY: 8.13802e5 Schub FY: 10001 CY: 0.125 | J: 0.000146484 IZZ: 8.13802e5 Schub FZ: 10001 CZ: 0.125 |
Materialeigenschaften: | Massendichte: 0 Massenspezifische Materialkosten: 0 Elastizitätsmodul: 3e7 | Querkontraktionszahl: 0.3 Wärmeausdehnung: 0 Leitfähigkeit: 0 |
Randbedingungen: | platziert auf Punkt A: konstant in allen FG | |
Last: | Position: | Betrag: |
axial | platziert auf Punkt B | FX=100 |
quer y | platziert auf Punkt B | FY=100 |
quer z | platziert auf Punkt B | FZ=100 |
1 Strukturbalken berücksichtigen Schub, das dargestellte theoretische Problem hingegen nicht. Dies wird durch die Werte für den Schubfaktor ausgeglichen.
Vergleich der Ergebnisdaten (Rhombusförmiger Balken)
Last | Messgröße | Theorie | Struktur | % Differenz |
|---|---|---|---|---|
Auslenkung an der Spitze: | ||||
axial | dmnd_d_x | 3.2e-3 | 3.2e-3 | 0 % |
quer y | dmnd_d_y | 3.6864e2 | 3.6864e2 | 0 % |
quer z | dmnd_d_z | 3.6864e2 | 3.6864e2 | 0 % |
Spannung: | ||||
Last | Messgröße | Theorie | Struktur | % Differenz |
axial | dmnd_s_ten | 3.2e3 | 3.2e3 | 0 % |
quer y | dmnd_s_bnd | 4.608e6 | 4.608e6 | 0 % |
quer z | dmnd_s_bnd | 4.608e6 | 4.608e6 | 0 % |
Last | Lkle Versch & DE | Max P | Anz. Gleichungen | |
|---|---|---|---|---|
Konvergenz: | ||||
axial | 0 % | 2 | 264 | |
quer y | 0 % | 2 | 264 | |
quer z | 0 % | 2 | 264 | |
Massiver kreisförmiger Balken
Spezifikationen
Art des Elements: | Massiver kreisförmiger Balken | |
Einheiten: | IPS | |
Bemaßungen: | r: 0.25 | |
Balkeneigenschaften: | Bereich: 0.19635 IYY: 0.00306796 Schub FY: 10001 CY: 0.25 | J: 0.00613592 IZZ: 0.00306796 Schub FZ: 10001 CZ: 0.25 |
Materialeigenschaften: | Massendichte: 0 Massenspezifische Materialkosten: 0 Elastizitätsmodul: 3e7 | Querkontraktionszahl: 0.3 Wärmeausdehnung: 0 Leitfähigkeit: 0 |
Randbedingungen: | platziert auf Punkt A: konstant in allen FG | |
Last: | Position: | Betrag: |
axial | platziert auf Punkt B | FX=100 |
quer y | platziert auf Punkt B | FY=100 |
quer z | platziert auf Punkt B | FZ=100 |
1 Strukturbalken berücksichtigen Schub, das dargestellte theoretische Problem hingegen nicht. Dies wird durch die Werte für den Schubfaktor ausgeglichen.
Vergleich der Ergebnisdaten (Massiver kreisförmiger Balken)
Last | Messgröße | Theorie | Struktur | % Differenz |
|---|---|---|---|---|
Auslenkung an der Spitze: | ||||
axial | crcl_d_x | 5.093e-4 | 5.092e-4 | 0.019% |
quer y | crcl_d_y | 9.77848 | 9.77995 | 0.015% |
quer z | crcl_d_z | 9.77848 | 9.77995 | 0.015% |
Spannung: | ||||
axial | crcl_s_ten | 5.093e2 | 5.092e2 | 0.019% |
quer y | crcl_s_bnd | 2.44462e5 | 2.44462e5 | 0 % |
quer z | crcl_s_bnd | 2.44462e5 | 2.44462e5 | 0 % |
Last | Lkle Versch & DE | Max P | Anz. Gleichungen | |
|---|---|---|---|---|
Konvergenz: | ||||
axial | 0 % | 2 | 264 | |
quer y | 0 % | 2 | 264 | |
quer z | 0 % | 2 | 264 | |
Hohler kreisförmiger Balken
Spezifikationen
Art des Elements: | Hohler kreisförmiger Balken | |
Einheiten: | IPS | |
Bemaßungen: | ri: 0.25 | |
Balkeneigenschaften: | Bereich: 0.147262 IYY: 0.00287621 Schub FY: 100001 CY: 0.25 | J: 0.00575243 IZZ: 0.00287621 Schub FZ: 10001 CZ: 0.25 |
Materialeigenschaften: | Massendichte: 0 Massenspezifische Materialkosten: 0 Elastizitätsmodul: 3e7 | Querkontraktionszahl: 0.3 Wärmeausdehnung: 0 Leitfähigkeit: 0 |
Randbedingungen: | platziert auf Punkt A: konstant in allen FG | |
Last: | Position: | Betrag: |
axial | platziert auf Punkt B | FX=100 |
quer y | platziert auf Punkt B | FY=100 |
quer z | platziert auf Punkt B | FZ=100 |
1 Strukturbalken berücksichtigen Schub, das dargestellte theoretische Problem hingegen nicht. Dies wird durch die Werte für den Schubfaktor ausgeglichen.
Vergleich der Ergebnisdaten (Hohler kreisförmiger Balken)
Last | Messgröße | Theorie | Struktur | % Differenz |
|---|---|---|---|---|
Auslenkung an der Spitze: | ||||
axial | hcr_d_x | 6.7906e-4 | 6.7906e-4 | 0 % |
quer y | hcr_d_y | 1.04304e1 | 1.04331e1 | 0.025% |
quer z | hcr_d_z | 1.04304e1 | 1.04332e1 | 0.026% |
Spannung: | ||||
axial | hcr_s_ten | 6.7906e2 | 6.7906e2 | 0 % |
quer y | hcr_s_bnd | 2.6076e5 | 2.6075e5 | 0.003% |
quer z | hcr_s_bnd | 2.6076e5 | 2.6076e5 | – |
Last | Lkle Versch & DE | Max P | Anz. Gleichungen | |
|---|---|---|---|---|
Konvergenz: | ||||
axial | 0 % | 2 | 264 | |
quer y | 0 % | 2 | 264 | |
quer z | 0 % | 2 | 264 | |
Ellipsenförmiger Balken
Spezifikationen
Art des Elements: | Ellipsenförmiger Balken | |
Einheiten: | IPS | |
Bemaßungen: | a: 1 b: 0.25 | |
Balkeneigenschaften: | Bereich: 0.785398 IYY: 0.19635 Schub FY: 10001 CY: 0.25 | J: 0.0461999 IZZ: 0.0122718 Schub FZ: 10001 CZ: 1 |
Materialeigenschaften: | Massendichte: 0 Massenspezifische Materialkosten: 0 Elastizitätsmodul: 3e7 | Querkontraktionszahl: 0.3 Wärmeausdehnung: 0 Leitfähigkeit: 0 |
Randbedingungen: | platziert auf Punkt A: konstant in allen FG | |
Last: | Position: | Betrag: |
axial | platziert auf Punkt B | FX=100 |
quer y | platziert auf Punkt B | FY=100 |
quer z | platziert auf Punkt B | FZ=100 |
1 Strukturbalken berücksichtigen Schub, das dargestellte theoretische Problem hingegen nicht. Dies wird durch die Werte für den Schubfaktor ausgeglichen.
Vergleich der Ergebnisdaten (Ellipsenförmiger Balken)
Last | Messgröße | Theorie | Struktur | % Differenz |
|---|---|---|---|---|
Auslenkung an der Spitze: | ||||
axial | elps_d_x | 1.2732e-4 | 1.2732e-4 | 0 % |
quer y | elps_d_y | 1.527887e-1 | 1.531516e-01 | 0.24 % |
quer z | elps_d_z | 2.4446 | 2.445098 | 0.02 % |
Spannung: | ||||
axial | elps_s_ten | 1.273239e2 | 1.27324e2 | 0 % |
quer y | elps_s_bnd | 1.527887e4 | 1.527887e4 | 0 % |
quer z | elps_s_bnd | 6.11155e4 | 6.111550e4 | 0 % |
Last | Lkle Versch & DE | Max P | Anz. Gleichungen | |
|---|---|---|---|---|
Konvergenz: | ||||
axial | 0 % | 2 | 264 | |
quer y | 0 % | 2 | 264 | |
quer z | 0 % | 2 | 264 | |
Hohler ellipsenförmiger Balken
Spezifikationen
Art des Elements: | Hohler ellipsenförmiger Balken | |
Einheiten: | IPS | |
Bemaßungen: | a: 1 b: 0.25 ai: 0.875 | |
Balkeneigenschaften: | Bereich: 0.184078 IYY: 0.081253 Schub FY: 10001 CY: 0.25 | J: 0.0191184 IZZ: 0.00507832 Schub FZ: 10001 CZ: 1 |
Materialeigenschaften: | Massendichte: 0 Massenspezifische Materialkosten: 0 Elastizitätsmodul: 3e7 | Querkontraktionszahl: 0.3 Wärmeausdehnung: 0 Leitfähigkeit: 0 |
Randbedingungen: | platziert auf Punkt A: konstant in allen FG | |
Last: | Position: | Betrag: |
axial | platziert auf Punkt B | FX=100 |
quer y | platziert auf Punkt B | FY=100 |
quer z | platziert auf Punkt B | FZ=100 |
1 Strukturbalken berücksichtigen Schub, das dargestellte theoretische Problem hingegen nicht. Dies wird durch die Werte für den Schubfaktor ausgeglichen.
Vergleich der Ergebnisdaten (Hohler ellipsenförmiger Balken)
Last | Messgröße | Theorie | Struktur | % Differenz |
|---|---|---|---|---|
Auslenkung an der Spitze: | ||||
axial | hel_d_x | 5.4325e-4 | 5.4324e-4 | 0.0018% |
quer y | hel_d_y | 3.6922e-1 | 3.7091e-1 | 0.45% |
quer z | hel_d_z | 5.9075 | 5.9091 | 0.027% |
Spannung: | ||||
axial | hel_s_ten | 5.4325e2 | 5.4324e2 | 0.0018% |
quer y | hel_s_bnd | 3.6922e4 | 3.6921e4 | 0.0027% |
quer z | hel_s_bnd | 1.4769e5 | 1.4768e5 | 0.0067% |
Last | Lkle Versch & DE | Max P | Anz. Gleichungen | |
|---|---|---|---|---|
Konvergenz: | ||||
axial | 0 % | 2 | 264 | |
quer y | 0 % | 2 | 264 | |
quer z | 0 % | 2 | 264 | |
mvss021:Dickwandiger Zylinder unter internem Druck
Analysetyp: | Statisch (Static) |
Modelltyp: | 3D |
Hintergrundinformation: | Roark, R.J., und Young, W.C. Formulas for Stress and Strain. NY: McGraw-Hill Book Co., 5. Auflage, Tabelle 32, Fall 1. |
Beschreibung: | Ein dickwandiger Zylinder, der internem Druck ausgesetzt ist, kann sich frei in allen Richtungen ausdehnen. Ermitteln Sie die maximale radiale Spannung und Umfangsspannung. |

Spezifikationen
Art des Elements: | Tetraeder (133) | |
Einheiten: | IPS | |
Bemaßungen: | Länge: 20 Ro: 6 Ri: 4 | |
Materialeigenschaften: | Masse-Dichte: 0.0002614 Massenspezifische Materialkosten: 0 Elastizitätsmodul: 1.06e7 | Querkontraktionszahl: 0.33 Wärmeausdehnung: 1.25e05 Leitfähigkeit: 9.254 |
Randbedingungen | Position | Freiheitsgrade |
|---|---|---|
constraint1 | platziert auf Punkt A: platziert auf Punkt B: platziert auf Punkt D: | konstant in VerschX, VerschY und VerschZ konstant in VerschY konstant in VerschY und VerschZ |
Lasten: | Ort/Betrag: | Verteilung | Räumliche Verteilung |
|---|---|---|---|
Druck | platziert auf allen Innenflächen: Druck = 1000 | Gesamtlast pro Flächeneinheit | gleichmäßig |
Vergleich der Ergebnisdaten
Theorie | Struktur | % Differenz | |
|---|---|---|---|
 yy entlang den Kanten C-E & F-G yy entlang den Kanten C-E & F-G | 2600 | 2603.7325 | 0.14% |
 xx entlang den Kanten C-E & F-G xx entlang den Kanten C-E & F-G | 1000 | 999.1724 | 0.08 % |
Mehrfach-Konvergenz %: Die Analyse konvergiert zu unter 1 % der Messwerte. | Max P: 6 | Anz. Gleichungen: 1875 | |
mvss022: Dünnwandiger kugelförmiger Behälter unter Eigengewicht
Analysetyp: | Statisch (Static) |
Modelltyp: | 3D Zyklische Symmetrie |
Hintergrundinformation: | Roark, R.J., und Young, W.C. Formulas for Stress and Strain. NY: McGraw-Hill Book Co., 5. Auflage, Tabelle 29, Fall 3c. |
Beschreibung: | Ein dünnwandiger halbkugelförmiger Behälter wird seinem Eigengewicht ausgesetzt (Gravitationslast). Ermitteln Sie die Gebindespannung an den Punkten A und B. |

Spezifikationen
Art des Elements: | Schalenelemente (3) | |
Einheiten: | IPS | |
Bemaßungen: | R: 10 | |
Materialeigenschaften: | Masse-Dichte: 0.0002588 Massenspezifische Materialkosten: 0 Elastizitätsmodul: 1.0e7 | Querkontraktionszahl: 0.3 Wärmeausdehnung: 0 Leitfähigkeit: 0 |
Randbedingungen | Position | Freiheitsgrade |
|---|---|---|
constraint1 | Kanten @  = 0 & = 0 &  = 90: = 90:Kante @ z = 0: Platziert auf Punkt C @ r = 10,  = 0, z = 0: = 0, z = 0: | Zyklische Symmetrie konstant in VerschZ konstant in VerschR, VerschT und VerschZ |
Last: | Richtung: | Betrag: |
|---|---|---|
Gravitation | x y z | 0.0 386.4 0.0 |
Vergleich der Ergebnisdaten
Theorie | Struktur | % Differenz | |
|---|---|---|---|
 zz an Punkt A: zz an Punkt A: | 1 | 0.987 | 1.3% |
 tt an Punkt B: tt an Punkt B: | -1 | -0.982 | 1.8% |
Adaptive Mehrfach-Konvergenz %: Die Analyse konvergiert zu unter 4.9 % der lokalen Verschiebung und der Element-Dehnungsenergie. Sie konvergiert zu 1.7 % der globalen RMS-Spannung. | Max P: 9 | Anz. Gleichungen: 773 | |
mvsl001: Statische Analyse zusammengesetzter Schichten
Analysetyp: | Statisch mit orthotropen Materialeigenschaften |
Modelltyp: | 3D |
Vergleich: | Theorie |
Hintergrundinformation: | Noor, A.K., und Mathers, M.D., "Shear-Flexible Finite-Element Models of Laminated Composite Plates and Shells." NASA TN D-8044; Langley Research Center, Hampton, Va. Dezember 1975. |
Beschreibung: | Ermitteln Sie das maximale Biegemoment und die Querverformung einer mit Spannpratzen befestigten orthotropen quadratischen Platte, die aus 9 Schichten besteht. |
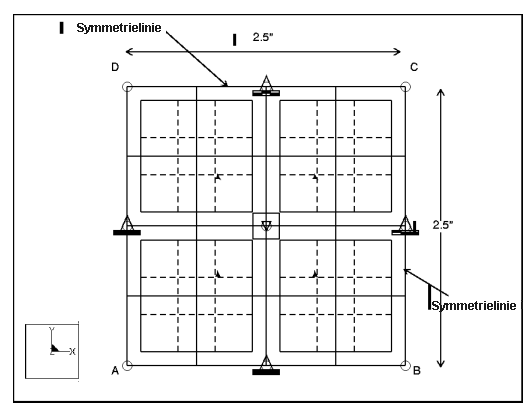
Spezifikationen
Art des Elements: | Schalenelement (4) | ||
Einheiten: | IPS | ||
Bemaßungen: | Länge: 2.5 Breite: 2.5 Dicke: 0.5 | ||
Schaleneigenschaften: | |||
Dehnsteifigkeit | A11=10.266 | A12=0.1252 | A16=0 |
A22=10.266 | A26=0 | ||
A66=0.3 | |||
Dehnbiegungs-Kopplungssteifigkeit | B11=0 | B12=0 | B16=0 |
B22=0 | B26=0 | ||
B66=0 | |||
Biegesteifigkeit | D11=0.25965 | D12=0.0026082 | D16=0 |
D22=0.1681 | D26=0 | ||
D66=0.00625 | |||
Querschubsteifigkeiten | A55=0.275004 | A45=0 | A44=0.275004 |
Masse pro Flächeneinheit | 7.2915e5 | ||
Rotationsträgheit pro Flächeneinheit | 1.5191e5 | ||
Wärmekoeffizienten: | |||
Kraft | N11=0 | N22=0 | N12=0 |
Moment | M11=0 | M22=0 | M12=0 |
Orte der Spannungsauswertung | CZ | Faserorientierung (Grad) | Material |
In Ergebnissen angegebene Position "Oben" | 0.25 | 0 | trniso1 |
In Ergebnissen angegebene Position "Unten" | 0.25 | 0 | trniso1 |
Materialeigenschaften: | |||
Masse-Dichte: 0.00014583 | Massenspezifische Materialkosten: 0 | ||
Elastizitätsmodule | E1=4e1 | E2=1 | E3=1 |
Querkontraktionszahl | Nu21=0.25 | Nu31=0.25 | Nu32=0 |
Schubmodule | G21=0.6 | G31=0.6 | G32= E2/[2*(1+Nu32)] |
Koeffizienten der Wärmeausdehnung | a1=0 | a2=0 | a3=0 |
Randbedingungen: | symmetrische Randbedingungen an Kanten B-C und C-D befestigt an Kanten A-B und A-D | ||
Lasten: | gleichmäßige Drucklast auf der Gesamtfläche = 1 | ||
Vergleich der Ergebnisdaten
Theorie | Struktur | % Differenz | |
|---|---|---|---|
Verschiebung (Displacement) | 11.596 | 11.84151 | 2.11% |
Biegemoment1 | 1.4094 | 1.41307 | 0.26 % |
Konvergenz %: 1.1 % der lokalen Verlagerung und Element-Dehnungsenergie und 2.2 % der globalen RMS-Spannung. | Max P: 3 | Anz. Gleichungen: 76 | |
1 Um dieses Ergebnis von Creo Simulate zu überprüfen, erstellen Sie ein Abfrageergebnisfenster für die Quantität Moment:Shell Resultant:XX. Öffnen Sie das Ergebnisfenster, und fragen Sie den Wert in der linken oberen Ecke des Modells ab. Sie erreichen dies durch View:Model Min. Der absolute Wert dieser negativen Zahl, der größer ist als der Wert, den Sie durch View:Model Max erhalten, wird hier angezeigt.