Equations des propriétés de type coque
Ce document décrit très brièvement la représentation mathématique des propriétés mécaniques des coques dans Creo Simulate. Il définit également la terminologie utilisée pour décrire les propriétés de type coque et les résultats de coque dans Creo Simulate.
Ce document est séparé selon les sections suivantes :
Rubrique
Présentation
Les formules indiquées dans ce document expriment les relations fondamentales entre les forces de type coque, moments, déformations, changements de courbure et propriétés et les résultats. Ces formules sont fournies pour définir sans ambigüité les conventions utilisées pour décrire les différentes données de modélisation et de résultats des coques.
Vous spécifiez des propriétés qui définissent le comportement mécanique des coques stratifiées sur la version de raideur du stratifié de la boîte de dialogue Définition de propriétés de type coque (Shell Property Definition). Pour en savoir plus, consultez la section A propos des propriétés de type coque. Au point pour lequel vous souhaitez afficher les résultats, vous définissez les propriétés suivantes relatives à l'orientation du matériau :
• raideur en dilatation de coque
• raideur en cisaillement transverse de coque
• raideur de couplage en traction-flexion de coque
• raideur en flexion de coque
• coefficient de moment thermique résultant de coque
• coefficient de force thermique résultante de coque
• masse par unité de surface
• inertie de rotation par unité de surface
Vous pouvez réviser les grandeurs de résultats suivantes par rapport à l'orientation du matériau au point d'intérêt ou par rapport à un repère. Pour en savoir plus, consultez la section Résultats relatifs.
• rotation du feuillet moyen de coque autour des axes X et Y
• déformation de feuillet moyen
• changement de courbure du feuillet moyen de coque
• moment résultant de coque
• force résultante de coque
• force de cisaillement transverse de coque
• contrainte
• déplacement du feuillet moyen de coque
Pour en savoir plus sur les symboles représentant ces termes, consultez la section Liste des symboles.
Ces formules et leurs descriptions n'ont pas pour but de constituer un didacticiel sur l'analyse de coques. Des informations plus détaillées sur la modélisation des coques stratifiées ou orthotropes sont disponibles dans les textes rédigés par Jones (1), Reddy (2), Tsai (3), Ugural (4) et d'autres. La section Bibliographie décrit ces textes.
Les figures et les équations présentées dans cette section sont données pour des coques plates ou des plaques. Les concepts d'ingénierie présentés ici sont une généralisation pour les coques courbées, mais les descriptions mathématiques des coques courbées sont plus compliquées et ne seront pas indiquées ici.
Formule de calcul des propriétés de type coque
Une coque est une section de votre modèle Creo Simulate. Elle est mince par rapport à sa largeur et à sa longueur. D'un point de vue du calcul, il est efficace de modéliser les régions minces de votre structure à l'aide de coques. Cette efficacité est en partie due à l'hypothèse de base concernant le comportement des coques. C'est-à-dire que le comportement mécanique d'une coque peut être approximé par la description du comportement mécanique du feuillet moyen de la coque.
Ainsi, le déplacement d'une coque peut être décrit par le déplacement et la rotation de son feuillet moyen, la déformation d'une coque peut être décrite par la déformation et les changements de courbure de son feuillet moyen et l'équilibre d'une coque peut être décrit par l'équilibre des contraintes intégrées par l'épaisseur de la coque.
La figure ci-dessous présente une coque rectangulaire plate dont les arêtes sont alignées avec les axes X et Y d'un repère cartésien. Le plan XY de ce repère est à mi-chemin entre les surfaces supérieure et inférieure de la coque, c'est-à-dire que le feuillet moyen de la coque est à z=0. La coque a une épaisseur t de sorte que la surface supérieure soit à z = t/2 et la surface inférieure à z = –t/2, comme illustré dans la figure suivante :

Comme mentionné ci-avant, l'hypothèse est acceptée que le déplacement d'un point (x, y, z) au niveau de la coque peut être exprimé en termes de déplacement et de rotation du point (x, y, 0) sur le feuillet moyen de la coque. Plus spécifiquement, il est accepté que :

où :
•  sont les composantes de déplacement dans les directions x, y et z respectivement ;
sont les composantes de déplacement dans les directions x, y et z respectivement ;
 sont les composantes de déplacement dans les directions x, y et z respectivement ;
sont les composantes de déplacement dans les directions x, y et z respectivement ;•  sont les composantes de déplacement du feuillet moyen ;
sont les composantes de déplacement du feuillet moyen ;
 sont les composantes de déplacement du feuillet moyen ;
sont les composantes de déplacement du feuillet moyen ;•  sont les (petites) rotations du feuillet moyen sur les axes x et y, respectivement.
sont les (petites) rotations du feuillet moyen sur les axes x et y, respectivement.
 sont les (petites) rotations du feuillet moyen sur les axes x et y, respectivement.
sont les (petites) rotations du feuillet moyen sur les axes x et y, respectivement.De la même façon, les composants de déformation  et
et  en tout point (x, y, z) peuvent être exprimés en termes de déformations du feuillet moyen (ou de la membrane) (
en tout point (x, y, z) peuvent être exprimés en termes de déformations du feuillet moyen (ou de la membrane) ( ) et de changements de courbure (
) et de changements de courbure ( ) comme suit :
) comme suit :
 et
et  en tout point (x, y, z) peuvent être exprimés en termes de déformations du feuillet moyen (ou de la membrane) (
en tout point (x, y, z) peuvent être exprimés en termes de déformations du feuillet moyen (ou de la membrane) ( ) et de changements de courbure (
) et de changements de courbure ( ) comme suit :
) comme suit :
Notez que l'Equation (A.2) contient les composants de déformation en cisaillement de tenseur,  et
et  , mais pas les composants de déformation en cisaillement d'ingénierie, qui correspondent au double des valeurs des composants de déformation en cisaillement de tenseur.
, mais pas les composants de déformation en cisaillement d'ingénierie, qui correspondent au double des valeurs des composants de déformation en cisaillement de tenseur.
 et
et  , mais pas les composants de déformation en cisaillement d'ingénierie, qui correspondent au double des valeurs des composants de déformation en cisaillement de tenseur.
, mais pas les composants de déformation en cisaillement d'ingénierie, qui correspondent au double des valeurs des composants de déformation en cisaillement de tenseur.Pour les coques plates, les composantes de déformation en cisaillement de tenseur sont les suivantes :

et

Les forces résultantes de la coque ( ), les moments résultants de la coque (
), les moments résultants de la coque ( ) et les forces de cisaillement transverse de la coque (
) et les forces de cisaillement transverse de la coque ( ) sont obtenus en intégrant les composants de contrainte
) sont obtenus en intégrant les composants de contrainte  à l'épaisseur de la coque. Les forces résultantes de coque sont données par :
à l'épaisseur de la coque. Les forces résultantes de coque sont données par :
 ), les moments résultants de la coque (
), les moments résultants de la coque ( ) et les forces de cisaillement transverse de la coque (
) et les forces de cisaillement transverse de la coque ( ) sont obtenus en intégrant les composants de contrainte
) sont obtenus en intégrant les composants de contrainte  à l'épaisseur de la coque. Les forces résultantes de coque sont données par :
à l'épaisseur de la coque. Les forces résultantes de coque sont données par :
Les moments résultants de coque sont donnés par :

Les forces de cisaillement transverse de coque sont données par :

La figure ci-dessous illustre les conventions relatives aux signes utilisées pour les forces et les moments résultants ainsi que les forces de cisaillement transverse. Notez qu'un moment positif,  , entraîne une déformation positive,
, entraîne une déformation positive,  , dans la moitié supérieure de la coque (z > 0) et une déformation négative dans la moitié inférieure de la coque (z < 0).
, dans la moitié supérieure de la coque (z > 0) et une déformation négative dans la moitié inférieure de la coque (z < 0).
 , entraîne une déformation positive,
, entraîne une déformation positive,  , dans la moitié supérieure de la coque (z > 0) et une déformation négative dans la moitié inférieure de la coque (z < 0).
, dans la moitié supérieure de la coque (z > 0) et une déformation négative dans la moitié inférieure de la coque (z < 0).
La relation entre les résultantes de coque d'un côté et les déformations de feuillet moyen et les changements de courbure de l'autre est donnée par :

et :

Dans l'équation (A.6), les grandeurs  (où i,j = 1, 2, 6) sont appelées raideurs en dilatation, les grandeurs
(où i,j = 1, 2, 6) sont appelées raideurs en dilatation, les grandeurs  sont appelées raideurs en flexion, les grandeurs
sont appelées raideurs en flexion, les grandeurs  sont appelées raideurs de couplage en traction-flexion et les grandeurs
sont appelées raideurs de couplage en traction-flexion et les grandeurs  (où k,l = 4,5) sont appelées raideur en cisaillement transverse. Les grandeurs
(où k,l = 4,5) sont appelées raideur en cisaillement transverse. Les grandeurs  et
et  représentent les déformations en cisaillement transverse au niveau du feuillet moyen. Les grandeurs
représentent les déformations en cisaillement transverse au niveau du feuillet moyen. Les grandeurs  et
et  représentent les forces thermiques et moments résultants respectivement.
représentent les forces thermiques et moments résultants respectivement.
 (où i,j = 1, 2, 6) sont appelées raideurs en dilatation, les grandeurs
(où i,j = 1, 2, 6) sont appelées raideurs en dilatation, les grandeurs  sont appelées raideurs en flexion, les grandeurs
sont appelées raideurs en flexion, les grandeurs  sont appelées raideurs de couplage en traction-flexion et les grandeurs
sont appelées raideurs de couplage en traction-flexion et les grandeurs  (où k,l = 4,5) sont appelées raideur en cisaillement transverse. Les grandeurs
(où k,l = 4,5) sont appelées raideur en cisaillement transverse. Les grandeurs  et
et  représentent les déformations en cisaillement transverse au niveau du feuillet moyen. Les grandeurs
représentent les déformations en cisaillement transverse au niveau du feuillet moyen. Les grandeurs  et
et  représentent les forces thermiques et moments résultants respectivement.
représentent les forces thermiques et moments résultants respectivement.Les résultantes de raideur et thermiques de coque introduites dans les équations (A.6) et (A.7) sont définies par l'intégration des propriétés de matériau de la coque sur l'épaisseur de la coque. Les raideurs en dilatation, flexion et traction-flexion sont données par :
 et :
et :
et :

où  sont les raideurs réduites du matériau.
sont les raideurs réduites du matériau.
 sont les raideurs réduites du matériau.
sont les raideurs réduites du matériau.La raideur en cisaillement transverse est donnée par :

où :
•  sont les raideurs (non réduites) du matériau et
sont les raideurs (non réduites) du matériau et
 sont les raideurs (non réduites) du matériau et
sont les raideurs (non réduites) du matériau et•  sont les coefficients de correction du cisaillement qui, pour une coque homogène, sont souvent
sont les coefficients de correction du cisaillement qui, pour une coque homogène, sont souvent 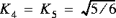 .
.
 sont les coefficients de correction du cisaillement qui, pour une coque homogène, sont souvent
sont les coefficients de correction du cisaillement qui, pour une coque homogène, sont souvent 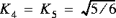 .
.Notez que si le matériau de la coque est distribué symétriquement sur le feuillet moyen, l'intégrale de l'équation (A.9) disparaît et les raideurs de couplage en traction-flexion  sont pareillement à zéro.
sont pareillement à zéro.
 sont pareillement à zéro.
sont pareillement à zéro.Les forces thermiques et les moments résultants sont donnés par :
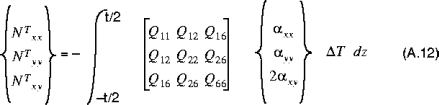
et :

où :
•  sont les coefficients de dilatation thermique du matériau et
sont les coefficients de dilatation thermique du matériau et
 sont les coefficients de dilatation thermique du matériau et
sont les coefficients de dilatation thermique du matériau et•  est le changement de température de l'état sans contrainte.
est le changement de température de l'état sans contrainte.
 est le changement de température de l'état sans contrainte.
est le changement de température de l'état sans contrainte.Si le changement de température est uniforme dans l'épaisseur de la coque,  dans les équations (A.12) et (A.13) peut être supprimé de l'intégrale, ce qui donne pour résultat les équations (A.14) et (A.15) :
dans les équations (A.12) et (A.13) peut être supprimé de l'intégrale, ce qui donne pour résultat les équations (A.14) et (A.15) :
 dans les équations (A.12) et (A.13) peut être supprimé de l'intégrale, ce qui donne pour résultat les équations (A.14) et (A.15) :
dans les équations (A.12) et (A.13) peut être supprimé de l'intégrale, ce qui donne pour résultat les équations (A.14) et (A.15) :

où  sont appelés les coefficients thermiques résultants de coque, donnés par :
sont appelés les coefficients thermiques résultants de coque, donnés par :
 sont appelés les coefficients thermiques résultants de coque, donnés par :
sont appelés les coefficients thermiques résultants de coque, donnés par :

Les propriétés massiques des coques sont également obtenues par l'intégration des données de propriété du matériau dans l'épaisseur de la coque. La masse par unité de surface,  , est donnée par :
, est donnée par :
 , est donnée par :
, est donnée par :
où  est la densité du matériau.
est la densité du matériau.
 est la densité du matériau.
est la densité du matériau.L'inertie de rotation par unité de surface,  , est donnée par :
, est donnée par :
 , est donnée par :
, est donnée par :
Liste des symboles
Le tableau suivant définit les symboles utilisés dans ce document :
Symbole | Définition |
|---|---|
 | coefficients de dilatation thermique |
 (i,j = 1,2,6) (i,j = 1,2,6) | raideur en dilatation de coque |
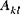 (k,l = 4,5) (k,l = 4,5) | raideur en cisaillement transverse de coque |
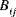 (i,j = 1,2,6) (i,j = 1,2,6) | raideur de couplage en traction-flexion de coque |
 | rotation du feuillet moyen de coque autour des axes X et Y |
 (k,l = 4,5) (k,l = 4,5) | raideur du matériau |
 (i,j = 1,2,6) (i,j = 1,2,6) | raideur en flexion de coque |
 | changement de température |
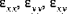 | déformation |
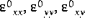 | déformation de feuillet moyen (ou membrane) |
 | changement de courbure du feuillet moyen de coque |
 (k,l = 4,5) (k,l = 4,5) | coefficients de correction du cisaillement |
 | moment résultant de coque |
 | moment thermique résultant de coque |
 | coefficient de moment thermique résultant de coque |
 | force résultante de coque |
 | force thermique résultante de coque |
 | coefficient de force thermique résultante de coque |
 | force de cisaillement transverse de coque |
 (i,j = 1,2,6) (i,j = 1,2,6) | raideur réduite du matériau |
 | masse par unité de surface |
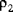 | inertie de rotation par unité de surface |
 | contrainte |
t | épaisseur de coque |
 | déplacement |
 | déplacement du feuillet moyen de coque |
x, y | coordonnées de feuillet moyen |
z | coordonnée perpendiculaire au feuillet moyen de coque |
Bibliographie
1. Jones, Robert M. Mechanics of Composite Materials. Washington, DC : Scripta Book Company, 1975.
2. Reddy, J.N. Energy and Variational Method in Applied Mechanics. New York : John Wiley & Sons, 1984.
3. Tsai, S. W. et H. T. Hahn Introduction to Composite Materials. Westport, CT : Technomic Publishing Co., 1980.
4. Ugural, A. C. Stresses in Plates and Shells. New York : McGraw-Hill Book Company, 1981.