Modélisation de l'érosion des particules
L'érosion est un phénomène entraînant une perte de matière due à l'impact répété de particules solides sur une surface. L'érosion endommage les tuyaux, les vannes et autres passage d'écoulement. Il est donc important d'étudier le taux d'érosion et d'identifier les zones susceptibles d'être érodées dans les passages d'écoulement.
La modélisation de l'érosion basée sur CFA comprend les étapes suivantes :
1. Les données de champ d'écoulement, telles que la vitesse, sont obtenues par la résolution des équations de Navier-Stokes.
2. Les particules sont libérées dans le champ d'écoulement et suivies individuellement pour obtenir des informations telles que la vitesse et l'angle d'impact.
3. Les informations d'impact des particules sont utilisées dans une équation d'érosion pour calculer le taux d'érosion ou la perte de la masse surfacique causée par les particules percutantes.
Les équations d'érosion étudient les effets de différents paramètres sur l'érosion :
Références : Mazdak Parsi et al. "A comprehensive review of solid particle erosion modeling for oil and gas wells and pipelines applications" (2014)
• Caractéristiques des particules, comme la taille, la forme, la densité, la dureté, etc.
• Informations concernant l'impact des particules, notamment la vitesse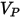 
ou l'angle d'impact 
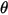, l'interaction particule-particule, etc.
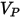ou l'angle d'impact 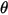, l'interaction particule-particule, etc.• Propriétés des parois cibles, notamment la densité de matière telles que la densité de matière, la dureté, etc.
Les équations d'érosion calculent le taux d'érosion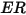 
, défini comme la quantité perdue de matière constituant une paroi (due à l'impact des particules solides) divisée par la masse des particules solides percutantes.
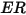, défini comme la quantité perdue de matière constituant une paroi (due à l'impact des particules solides) divisée par la masse des particules solides percutantes.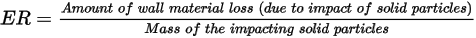
Creo Flow Analysis utilise les modèles d'érosion détaillés aux sections suivantes :
Références : Mazdak Parsi etc. "CFD simulation of sand particle erosion in gas-dominant multiphase flow" (2015)
Modèle de Finne
L'équation d'érosion de Finne est la suivante :
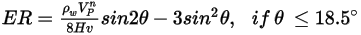
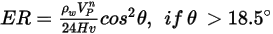
où,
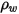 | Densité de matière constituant la paroi (kg/m3) |
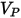 | Vitesse d'impact des particules (m/s) |
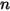 | Exposant de vitesse (égal à 2 pour la plupart des applications industrielles) |
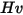 | Dureté Vickers (Pa) |
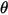 | Angle d'impact (degré) |
 | Ce modèle sous-estime l'enlèvement de matière pour les angles d'impact de particules supérieurs à 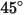 et aucune érosion n'est prévue pour les impacts normaux. |
Modèle de Zhang
L'équation d'érosion de Zhang est la suivante :
où,
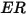 | Taux d'érosion |
 |  |
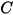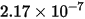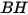 | Dureté Brinell de la matière constituant la paroi (Pa) |
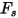 | Facteur de forme des particules |
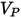 | Vitesse d'impact des particules (m/s) |
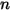 | Exposant de vitesse (égal à 2.41) |
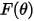 | Fonction d'angle d'impact |
Le facteur de forme des particules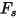 
possède les valeurs suivantes pour les différents types de particules de sable :
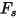possède les valeurs suivantes pour les différents types de particules de sable :Valeur | Type de particule de sable |
|---|---|
1.0 | Abrasive ou angulaire |
0.53 | Semi-arrondie |
0.2 | Entièrement arrondie |
La fonction d'angle d'impact est donnée comme suit :
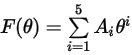
Le tableau suivant répertorie les valeurs de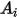 
:
: |  |  |  |  |
|---|---|---|---|---|
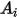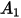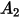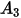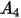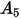5.40 | -10.11 | 10.93 | -6.33 | 1.42 |
Modèle d'Oka
L'équation d'érosion d'Oka et al. est la suivante :
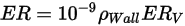
Equation 2.406
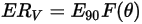
Equation 2.407
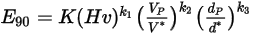
Equation 2.408
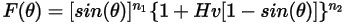
Equation 2.409
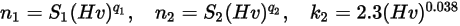
Equation 2.410
où,
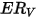 | Taux d'érosion volumétrique (mm3/kg) |
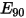 | Dommages de l'érosion à un angle d'impact normal (mm3/kg) |
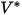 | Vitesse d'impact de référence (m/s) |
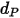 | Diamètre des particules (m) |
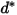 | Diamètre des particules de référence (m) |
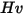 | Dureté Vickers (GPa) |
Les valeurs des différents coefficients utilisés dans l'équation 2.406, l'équation 2.407, l'équation 2.408, l'équation 2.409 et l'équation 2.410 apparaissent dans le tableau suivant :
 |  |  |  |  |  |  |
|---|---|---|---|---|---|---|
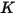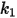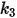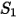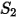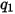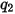60 | -0.12 | 0.19 | 0.71 | 2.4 | 0.14 | -0.94 |
Modèle de DNV
L'équation d'érosion de DNV est la suivante :
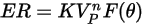
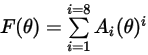
où,
 |  |
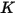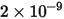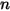 (exposant de vitesse) |  |
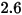Le tableau ci-dessous répertorie les valeurs de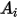 
:
: |  |  |  |  |  |  |  |
|---|---|---|---|---|---|---|---|
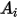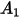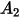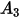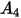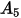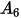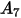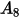9.370 | -42.295 | 110.864 | -175.804 | 170.137 | -98.398 | 31.211 | -4.170 |
Modèle de Mansouri
Mansouri a développé l'équation d'érosion suivante :
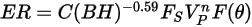
Equation 2.413
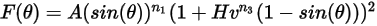
Equation 2.414
où,
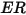 | Taux d'érosion |
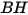 | Dureté Brinell de la matière constituant la paroi (Pa) |
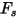 | Facteur de forme des particules |
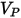 | Vitesse d'impact des particules (m/s) |
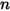 | Exposant de vitesse |
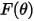 | Fonction d'angle d'impact |
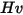 | Dureté Vickers (Pa) |
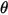 | Angle d'impact (degré) |
Le tableau suivant contient les valeurs des différents paramètres utilisés dans l'équation 2.413 et l'équation 2.414 de l'équation d'érosion de Mansouri (2015).
 |  |  |  |  |  |
|---|---|---|---|---|---|
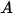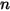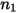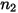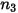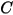0.6947 | 2.41 | 0.2 | 0.85 | 0.65 | 4.49e-07 |
Modèle de Grant-Tabakoff
L'équation d'érosion du modèle de Grant-Tabakoff est la suivante :
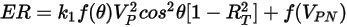
Equation 2.415
où,
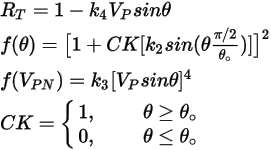
Equation 2.416
où,
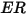 | Taux d'érosion |
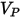 | Vitesse d'impact des particules (m/s) |
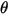 | Angle d'impact (degré) |
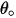 | Angle d'érosion maximale (degré) |
Le taux d'érosion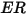 
dans l'équation 2.415 est défini comme la quantité, en milligramme, de matière enlevée par unité de masse (gramme) de particules percutantes. L'unité de vitesse est le ft/s.
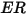dans l'équation 2.415 est défini comme la quantité, en milligramme, de matière enlevée par unité de masse (gramme) de particules percutantes. L'unité de vitesse est le ft/s.
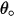correspond à l'angle d'érosion maximale. Par exemple, 
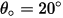pour un alliage à base d'aluminium.Les valeurs des différents coefficients du modèle de Grant-Tabakoff sont répertoriées dans le tableau suivant :
 |  |  |  |
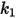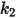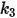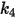3.67e-06 | 0.585 | 6e-12 | 0.0016 |