Fonctions
Les fonctions suivantes de l'Editeur d'expression (Expression Editor) permettent la manipulation mathématique et logique des vecteurs et des scalaires :
• Opérateurs
◦ Communs aux vecteurs et aux scalaires, tels que l'addition et la soustraction
◦ Scalaires uniquement, tels que les racines carrées et les logarithmes
◦ Vecteurs uniquement, tels que les produits scalaires et vectoriels
• Fonctions logiques
• Fonctions trigonométriques et hyperboliques
• Autres fonctions
• Tables
Opérateurs
Les opérateurs permettent la manipulation mathématique des vecteurs et des scalaires. Dans le tableau ci-après, a b et c sont des scalaires, et U, V et W des vecteurs.
|
Opérateurs d'expression
|
Fonction
|
Exemple
|
|---|---|---|
|
Opérateurs : scalaires et/ou vecteurs
|
||
|
Addition
|
a = b+c ou V = U+W
|
|
|
Soustraction
|
a = b-c ou V = U-W
|
|
|
*
|
Multiplication de deux scalaires ou d'un scalaire et d'un vecteur
|
a = b*c ou V = a*U (mais pas V = U*W)
|
|
Opérateur : scalaires uniquement
|
||
|
/
|
Division
|
a = b/c
|
|
exp(scalaire)
|
Fonction exponentielle de base e
|
a = exp(b) élève e à la puissance de b : a= eb
|
|
ln(scalaire)
|
Fonction de logarithme naturel pour e
|
a = ln(b) renvoie le logarithme naturel de b
|
|
sqrt(scalaire)
|
Fonction racine carrée
|
a = sqrt(b)
|
|
^
|
Fonction exponentielle
|
a= b^c élève b à la puissance de c : a= bc
|
|
Opérateur : vecteurs uniquement
|
||
|
&
|
Produit scalaire d'un vecteur
|
a = V&U (a = |V| |U| cos (angle))
|
|
^
|
Produit vectoriel d'un vecteur
|
V=U^W (|V| = |U| |W| x sin (angle) 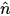 ), la règle de la main droite est appliquée. ), la règle de la main droite est appliquée. |
|
len(vecteur)
|
Renvoie la longueur du vecteur V
|
a = len(V)
|
|
normalize(vecteur)
|
Renvoie un vecteur unitaire normalisé V/|V|
|
V = normalize(U)
|
|
rotate(vecteur,angle,direction,centre)
|
Renvoie un vecteur pivoté en fonction de l'angle de rotation, de la règle de la main droite, de l'axe de rotation et d'un centre de rotation facultatif. (Si aucun centre n'est défini, la valeur par défaut est 0,0,0.)
|
Vrot = rotate(V,alpha,U,W), où V correspond au vecteur à faire pivoter, alpha à l'angle exprimé en radians et U à l'axe de rotation. La règle de la main droite est appliquée. W est un point central facultatif défini comme vecteur.
|
Fonctions logiques
Les fonctions logiques permettent d'inclure des instructions logiques.
|
Opérateurs d'expression
|
Fonction
|
Exemple
|
|---|---|---|
|
true
|
vrai logique
|
|
|
false
|
faux logique
|
|
|
<
|
inférieur à
|
|
|
>
|
supérieur à
|
|
|
==
|
Egal en comparaison logique
|
a = (b==3) ? 1 : 2
|
|
ou
|
ou logique
|
|
|
et
|
et logique
|
|
|
!
|
négation logique
|
!< pas inférieur à
|
|
a = expression ? b : c
|
a = b si l'expression est vraie ;
a = c si l'expression est fausse
|
a = (b>3) ? 1 : 2 ==> (si b est supérieur à 3, a = 1, sinon a = 2)
|
Fonctions trigonométriques et hyperboliques
Les fonctions trigonométriques et hyperboliques permettent d'inclure les fonctions correspondantes dans les instructions mathématiques.
|
Expressions transcendantes
|
Fonction
|
|---|---|
|
Trigonométriques
|
|
|
sin(radians)
|
Fonction sinus
|
|
cos(radians)
|
Fonction cosinus
|
|
cot(radians)
|
Fonction cotangente
|
|
tan(radians)
|
Fonction tangente
|
|
asin ()
|
Fonction sinus inverse, renvoie une valeur en radians
|
|
acos ()
|
Fonction cosinus inverse, renvoie une valeur en radians
|
|
acot()
|
Fonction cotangente inverse, renvoie une valeur en radians
|
|
atan ()
|
Fonction tangente inverse, renvoie une valeur en radians
|
|
atan2(y,x)
|
Fonction tangente inverse à deux variables (-pi, pi), renvoie une valeur en radians
|
|
Hyperboliques
|
|
|
sinh ()
|
Fonction sinus hyperbolique
|
|
cosh ()
|
Fonction cosinus hyperbolique
|
|
coth()
|
Fonction cotangente hyperbolique
|
|
tanh ()
|
Fonction tangente hyperbolique
|
|
asinh()
|
Fonction sinus hyperbolique inverse
|
|
acosh()
|
Fonction cosinus hyperbolique inverse
|
|
acoth()
|
Fonction cotangente hyperbolique inverse
|
|
atanh()
|
Fonction tangente hyperbolique inverse
|
Fonctions associées à l'affichage
Les fonctions associées à l'affichage s'appliquent au panneau Affichage (Display). Elles vous permettent d'effectuer les opérations suivantes :
• Activer la création d'une nouvelle variable avec toutes les fonctions d'une variable dérivée. Les fonctions incluent la possibilité d'afficher cette fonction sur des entités géométriques telles que des frontières et des isosurfaces.
• Accéder aux variables aux points de contrôle
• Définir des variables utilisateur pour les tracés XY
Variables définies par l'utilisateur pour l'affichage 3D
display.varname : définit les variables utilisateur telles que les contours, les isosurfaces et les vecteurs des tracés 3D. La nouvelle variable apparaît dans le panneau Propriétés (Properties) sous Variable (Variable) dans l'onglet Vue (View).
#display.varname: dispname [unit] : (facultatif) définit un nouveau nom avec son unité pour une variable d'affichage définie par l'utilisateur.
Exemple :
display.pref = flow.P - 101325
#display.pref : pression manométrique [Pa]
Lorsque vous utilisez ces expressions, l'entité de pression manométrique apparaît sous les valeurs de la propriété Variable (Variable), comme illustré ci-dessous.
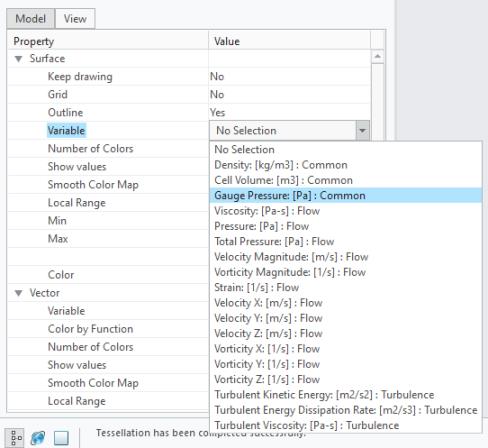
Variables aux points de contrôle
Vous pouvez accéder aux variables de cellule locales à n'importe quel point de contrôle en utilisant le format suivant :
module[.subname].var@probe.name
Coordonnées du point :
probe.coord@probe_name
Exemple :
inletP = flow.P@probe."Point01"+101325
Variable défini par l'utilisateur pour le tracé XY
plot.varname : définit une variable utilisateur que vous pouvez utiliser dans les tracés XY. La nouvelle variable commune est ajoutée en tant que valeur pour la propriété Variable (Variable) dans le panneau Propriétés (Properties).
#plot.varname: dispname [unit] : (Facultatif) définit un nouveau nom avec unité pour une variable définie par l'utilisateur.
Exemple :
plot.head = (flow.pt@outlet - flow.pt@inlet)/998/9.8
#plot.head: hauteur de charge[m]
• N'ajoutez pas d'espace avant le signe deux-points lorsque vous définissez un nouveau nom de variable d'affichage ou de tracé et une unité. • Les unités par défaut des variables d'affichage et de tracé apparaissent entre crochets. Par exemple, l'unité par défaut Pa s'affiche pour la variable de pression. Si vous définissez une unité correctement, l'unité s'affiche à l'écran. Dans cet exemple, lorsque vous changez l'unité finale qui apparaît, ses valeurs sont également converties. Si vous ne définissez pas l'unité correctement, le logiciel ignore l'unité. |
Autres fonctions
Opérateurs d'expression | Fonction | Exemple |
|---|---|---|
abs(x) | Fonction valeur absolue | |
max(x,y) | Fonction maximale | a=max(b,c) ==> a=b si b>c ou a=c si c>=b |
min(x,y) | Fonction minimale | a=min(b,c) ==> a=b si b<c ou a=c si c<=b |
mod(x,y) | Fonction modulo | a=mod(c,b) ==> a = le reste de c divisé par b |
sgn(x) | Renvoie un marqueur (-1, 0 ou 1) indiquant le signe | a=sgn(b) ==> a= -1 si b<0 a = 0 si b=0 a = 1 si b>0 |
step(x) | Une fonction en escalier renvoie 0 ou 1 en fonction de la valeur par rapport à zéro | a= step(b) ==> a = 0 si b<0 a = 1 si b>=0 |
Tables
La fonction de table permet d'inclure des données à partir de fichiers de table externes situés dans le même répertoire que le fichier de projet (*.spro).
Expressions de table | Fonction |
|---|---|
table(nom de fichier,x) | Interpole à partir d'une table à une dimension |
table(nom de fichier,x,y) | Interpole à partir d'une table à deux dimensions |
Exemple :
Utilisation de tables :
# Extraction d'informations dans les tables
p = table("inlet_pressure.txt",temps)
densité = table("R134a_density.txt",température,pression)
• Format de table : une dimension (nom de fichier,x) : permet d'accéder à une table de données à une dimension située dans le même répertoire que le fichier de projet (*.spro).
◦ Format de table à une dimension pour une distribution uniforme
<?xml version="1.0" encoding="ISO-8859-1"?>
<table size="n" min="xmin" max="xmax" outside="flat | extrapolation">
# comments (x assumed to have uniform distribution)
v1
v2
...
vn
</table/>
<table size="n" min="xmin" max="xmax" outside="flat | extrapolation">
# comments (x assumed to have uniform distribution)
v1
v2
...
vn
</table/>
◦ Format de table à une dimension pour une distribution non uniforme
<?xml version="1.0" encoding="ISO-8859-1"?>
<table size="n" outside="flat | extrapolation">
# You can add comments by putting the hashmark “#” in front .. but do not insert comments before the xml line (line 1)
x1 v1
x2 v2
xn vn
</table/>
<table size="n" outside="flat | extrapolation">
# You can add comments by putting the hashmark “#” in front .. but do not insert comments before the xml line (line 1)
x1 v1
x2 v2
xn vn
</table/>
Dans le format, outside = “flat” or outside = "extrapolation", sous la balise table, définit la façon dont une valeur est déterminée lorsque l'entrée x, y est hors limites.
• Format de table : deux dimensions (nom de fichier,x,y) : permet d'accéder à une table de données à deux dimensions située dans le même répertoire que le fichier de projet (*.spro).
◦ Format de table à deux dimensions pour une distribution uniforme
<?xml version="1.0" encoding="ISO-8859-1"?>
<table size="nx my" min="xmin ymin" max="xmax ymax" outside="flat | extrapolation">
# comment
# values table (x and y assumed to have uniform distribution
v(x1,y1) v(x2,y1) … v(xn,y1)
v(x1,y2) v(x2,y2) … v(xn,y2)
...
v(x1,ym) v(x2,ym) … v(xn,ym)
</table>
<table size="nx my" min="xmin ymin" max="xmax ymax" outside="flat | extrapolation">
# comment
# values table (x and y assumed to have uniform distribution
v(x1,y1) v(x2,y1) … v(xn,y1)
v(x1,y2) v(x2,y2) … v(xn,y2)
...
v(x1,ym) v(x2,ym) … v(xn,ym)
</table>
◦ Format de table à deux dimensions pour une distribution non uniforme
<?xml version="1.0" encoding="ISO-8859-1"?>
<table size="nx my" outside ="flat | extrapolation">
# x and y variable ranges
x1 x2 … xn
y1 y2 … ym
# values table
v(x1,y1) v(x2,y1) … v(xn,y1)
v(x1,y2) v(x2,y2) … v(xn,y2)
...
v(x1,ym) v(x2,ym) … v(xn,ym)
</table>
<table size="nx my" outside ="flat | extrapolation">
# x and y variable ranges
x1 x2 … xn
y1 y2 … ym
# values table
v(x1,y1) v(x2,y1) … v(xn,y1)
v(x1,y2) v(x2,y2) … v(xn,y2)
...
v(x1,ym) v(x2,ym) … v(xn,ym)
</table>
Dans le format, outside = “flat” or outside = "extrapolation", sous la balise table, définit la façon dont une valeur est déterminée lorsque l'entrée x, y est hors limites.
Pour ajouter un commentaire, placez une dièse ("#") devant le texte. N'insérez pas de commentaires avant la ligne xml (ou ligne 1). |