Modèles eulériens et équations principales
Cette section décrit les équations principales pour les modèles multiphases de mélange et VOF, et la modélisation de turbulence et des frontières dans les écoulements multiphases.
Equations principales multiphasiques générales
Dans l'approche d'Euler-Euler, les différents composants ou phases d'un système multiphase sont considérés comme des continuums interpénétrants sur le plan mathématique qui partagent la même pression d'écoulement. Etant donné que toutes les phases partagent l'espace physique ou le volume, cette approche introduit le concept de fraction volumique de phase pour décrire le transport des phases. Les fractions volumiques de phase sont considérées comme des fonctions continues de l'espace et du temps, et leur somme est égale à 1. On applique les lois de conservation pour chaque phase afin d'élaborer un ensemble d'équations principales qui sont fermées par des relations constitutives théoriques ou empiriques. Dans le cadre de l'approche d'Euler-Euler, deux types de modèles sont communément utilisés :
• Modèle à plusieurs fluides eulérien ou non homogène : résout directement les équations principales sur chaque phase, incluant les équations d'énergie cinétique, d'énergie, de turbulence, d'espèce et de fraction volumique. Les interactions entre phases, à savoir les transferts d'énergie cinétique, de masse, d'espèce et de chaleur interphase, sont modélisées par des sous-modèles physiques.
En utilisant le scalaire de phase général, ϕq, q pour la nième phase q, l'équation généralisée pour la phase q présente la forme suivante :
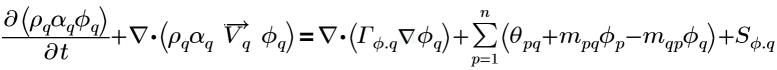
équation 2.54
où,
ρq | Densité q |
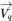 | vitesse |
Sϕq | Terme source |
Tϕq | Coefficient de diffusion |
αq | Fraction volumique dans la nième phase q |
et ϕq représente les variables dépendantes dans un système multiphasique :
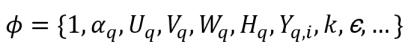
équation 2.55
où,
Uq, Vq, Wq | Composantes de vitesse de phase |
Hq | Enthalpie totale de phase |
Yqi | Fraction massique de l'espèce "i" dans la nième phase q |
k | énergie cinétique turbulente |
ε | Taux de dissipation d'énergie cinétique turbulente pour les modèles k-ε |
Dans l'équation 2.54, le second terme du côté droit représente les échanges interphase. Plus précisément :
p | nième phase p |
n | Nombre de phases dans le système multiphasique |
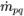 | Transfert de masse entre la nième phase q et la nième phase q |
θpq | Echange direct entre phases des grandeurs de transport incluant l'énergie cinétique, l'énergie et l'espèce |
L'utilisation de sous-modèles pour les échanges interphase d'espèce, de masse, d'énergie cinétique et de chaleur vous permet d'élaborer l'ensemble complet d'équations principales d'écoulement à partir des équations de transport qui sont généralisées ici.
• Modèle multiphasique homogène : alternative simplifiée et plus économique au modèle non homogène. L'approche de modélisation homogène consiste à moyenner les équations principales d'écoulement, d'énergie et de turbulence de phase de manière à produire un ensemble d'équations de transport de mélange, tout en continuant à résoudre les fractions volumiques de phase. Pour le scalaire de mélange, ϕm, l'équation principale généralisée est exprimée comme suit :
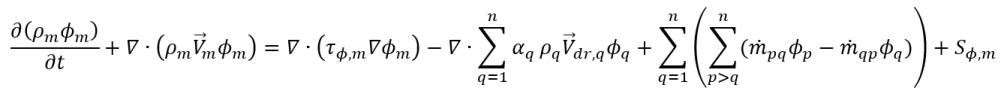
équation 2.56
où,
m | Mélange de phases |
Toutes les variables avec m | Valeurs moyennées de mélange ou de phase |
et 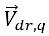 correspond à la différence entre la vitesse de la phase q et la vitesse du mélange :
correspond à la différence entre la vitesse de la phase q et la vitesse du mélange :
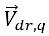 correspond à la différence entre la vitesse de la phase q et la vitesse du mélange :
correspond à la différence entre la vitesse de la phase q et la vitesse du mélange :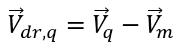
Le modèle multiphasique homogène est un cas limite de l'écoulement multiphasique d'Euler-Euler dans lequel le taux de transfert interphase est important. Il repose sur l'hypothèse fondamentale selon laquelle toutes les phases partagent le même champ de pression. Grâce à cette hypothèse, le modèle homogène favorise la simplification du modèle à plusieurs fluides eulérien non homogène en supposant que toutes les phases partagent un même champ de vitesse, de température et de turbulence. Cette approche constitue une bonne alternative au modèle à plusieurs fluides eulérien complet grâce à sa facilité d'implémentation et aux économies de calcul qu'elle permet de réaliser. Sur le plan physique, en évitant la nécessité de recourir à des modèles d'échange interphase dans les équations d'énergie cinétique et d'énergie, le modèle homogène peut se révéler tout aussi efficace que le modèle à plusieurs fluides complet dans des cas tels que les écoulements à surface libre (VOF), la cavitation ou d'autres écoulements multiphases très variés.
Dans Creo Flow Analysis, le module multiphase actuel adopte uniquement l'approche de modélisation homogène. Il se concentre sur la modélisation des écoulements à surface libre (modèle VOF) et des écoulements diphasiques liquide-gaz homogènes (modèle de mélange). En principe, vous pouvez appliquer cette fonctionnalité de modélisation aux écoulements à n phases.
Modèles multiphasiques de mélange et VOF
Les modèles multiphases de mélange et VOF utilisent l'approche de modélisation homogène. L'équation de transport de la fraction volumique à chaque phase est obtenue à partir de l'équation 2.54. Les équations principales d'énergie cinétique et d'énergie du mélange dérivent de l'utilisation de l'équation 2.56 et des lois de conservation de la masse, de l'énergie cinétique et de l'énergie. L'ensemble d'équations principales est présenté dans cette section.
• Equation de fraction volumique de la phase q
Dans l'équation 2.54, la définition de ϕq=1 obtient l'équation de fraction volumique de la phase q :
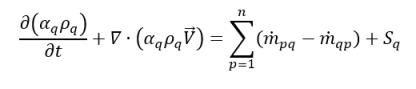
équation 2.57
où les termes de vitesse d'échange de masse 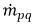 et
et 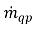 représentent respectivement l'intensité de la source et du puits pour la phase q. Dans un processus de transfert de masse interphase, l'un de ces deux termes est généralement nul. Considérez l'exemple suivant :
représentent respectivement l'intensité de la source et du puits pour la phase q. Dans un processus de transfert de masse interphase, l'un de ces deux termes est généralement nul. Considérez l'exemple suivant :
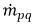 et
et 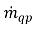 représentent respectivement l'intensité de la source et du puits pour la phase q. Dans un processus de transfert de masse interphase, l'un de ces deux termes est généralement nul. Considérez l'exemple suivant :
représentent respectivement l'intensité de la source et du puits pour la phase q. Dans un processus de transfert de masse interphase, l'un de ces deux termes est généralement nul. Considérez l'exemple suivant :Dans un processus d'évaporation, la phase liquide q perd de la masse, 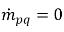 et
et 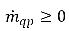 , alors que dans la phase vapeur,
, alors que dans la phase vapeur, 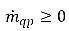 et
et 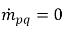 .
.
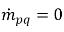 et
et 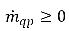 , alors que dans la phase vapeur,
, alors que dans la phase vapeur, 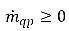 et
et 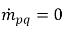 .
.Dans le cas d'un système à n phases, une somme des fractions volumiques de phase satisfait à la contrainte physique :
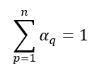
équation 2.58
Ou la conservation de la masse totale :
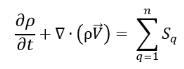
équation 2.59
où les grandeurs du mélange sont définies comme suit :
◦ Densité volumique moyenne du mélange
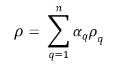
équation 2.60
◦ Vitesse massique moyenne du mélange :
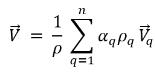
équation 2.61
• Equation d'énergie cinétique du mélange : s'obtient en additionnant les équations d'énergie cinétique de toutes les phases du système. Dans l'équation 2.56, lorsque vous définissez 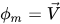 , vous obtenez
, vous obtenez
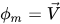 , vous obtenez
, vous obtenez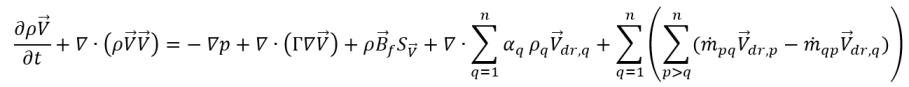
équation 2.62
où les grandeurs du mélange sont définies ci-après :
◦ Viscosité volumique moyenne du mélange :

équation 2.63
Le coefficient de diffusion Γ dans l'équation 2.62 est calculé à l'aide de la viscosité dynamique du mélange μ et de la viscosité turbulente μt. Les deux derniers termes sur la droite représentent l'échange d'énergie cinétique induit par le transfert d'énergie cinétique direct et par le transfert de masse. Ils sont déterminés par les vitesses de dérive de phase 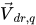 définies sous la forme :
définies sous la forme :
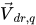 définies sous la forme :
définies sous la forme :
équation 2.69
Dans l'approche homogène, vous pouvez modéliser cette vitesse de dérive à l'aide d'un modèle algébrique. Toutefois, le modèle de mélange et VOF actuel ne suppose aucun glissement entre les phases :
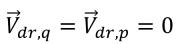
Par conséquent, les deux termes d'échange d'énergie cinétique sont nuls.
◦ Equation d'énergie du mélange
Sans vitesse de glissement, l'équation d'énergie du mélange prend la forme suivante :
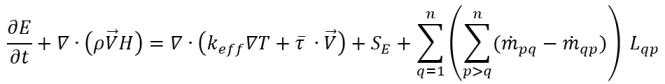
équation 2.70
où les variables du mélange sont définies ci-après :
▪ Conductivité thermique volumique moyenne
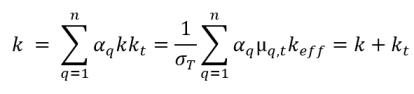
équation 2.71
▪ Energie et enthalpie massiques moyennes du mélange
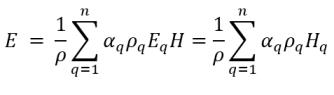
équation 2.72
Dans l'équation 2.70 d'énergie du mélange, le terme d'échauffement visqueux, 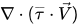 , est calculé comme dans l'écoulement monophase, et SE est la source de chaleur externe/utilisateur totale.
, est calculé comme dans l'écoulement monophase, et SE est la source de chaleur externe/utilisateur totale.
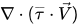 , est calculé comme dans l'écoulement monophase, et SE est la source de chaleur externe/utilisateur totale.
, est calculé comme dans l'écoulement monophase, et SE est la source de chaleur externe/utilisateur totale.Le dernier terme sur la droite correspond au transfert de chaleur sur l'interface causé par le transfert de masse. En partant du principe que les phases partagent la même température, le terme Lgp dépend de la définition de Hq et de Hp dans l'équation d'énergie résolue.
Comme décrit dans le module Chaleur (Heat), l'enthalpie statique d'un matériau comporte deux parties : l'enthalpie de référence d'état standard et l'enthalpie sensible. Si vous supposez que la phase q et la phase p correspondent aux phases liquide et vapeur, les enthalpies statiques totales de phase sont les suivantes :
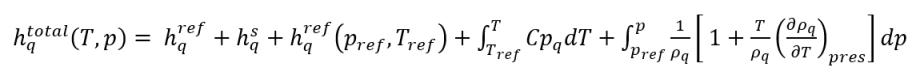
équation 2.73
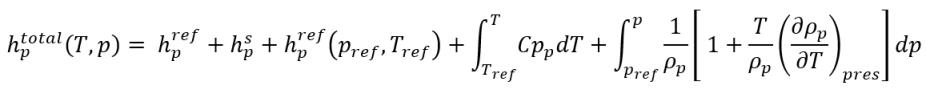
équation 2.74
où,
pref | pression de référence |
Tref | température de référence |
hq,ref | enthalpies de référence d'état standard de phase q |
hp,ref | enthalpies de référence d'état standard de phase p |
La différence des enthalpies de référence
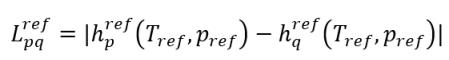
équation 2.75
correspond à la chaleur latente à la température de référence Tref et à la pression de référence pref.
▪ Inclusion de l'enthalpie de référence standard :
Dans l'équation 2.70, si l'enthalpie H désigne l'enthalpie totale du mélange, vous avez :
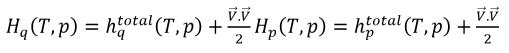
équation 2.76
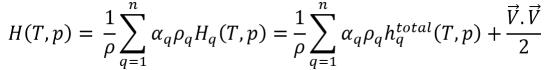
équation 2.77
La différence due aux enthalpies de formation de phase ou la chaleur latente, Lpq, a déjà été incluse dans l'équation d'énergie. La grandeur est définie sur zéro :
Lpq = 0
Et le transfert de chaleur découlant du transfert de masse, qui correspond au dernier terme à droite de l'équation 2.70, est nul dans l'équation d'énergie du mélange.
▪ Exclusion de l'enthalpie de référence standard :
Dans un solveur de mécanique des fluides numérique, l'enthalpie totale n'est pas résolue directement. A la place, seule l'enthalpie sensible relative à la température de saturation est incluse dans l'enthalpie résolue et l'énergie interne :
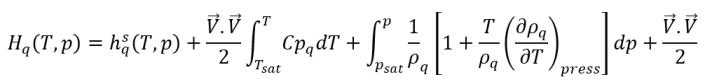
équation 2.79
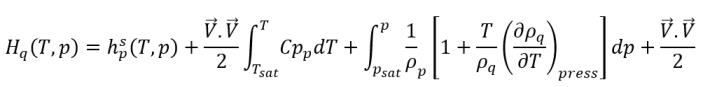
équation 2.80
La valeur Lpq n'est pas nulle. Il doit correspondre à la chaleur latente :
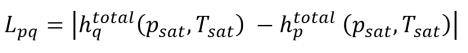
équation 2.81
où,
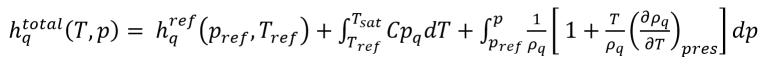
équation 2.82
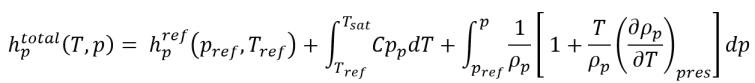
équation 2.83
Dans Creo Flow Analysis, l'enthalpie de référence d'état standard est automatiquement prise en compte par défaut. Aucune entrée utilisateur n'est requise.
Modèles de turbulence
• Modèles de turbulence k-ε du mélange
Les modèles multiphases de mélange et VOF prennent en compte l'effet de turbulence sur le mélange des phases en utilisant les extensions des modèles de turbulence monophases. Les modèles de turbulence et les traitements à proximité de la paroi, décrits dans le module Turbulence (Turbulence), sont étendus aux écoulements multiphases dans Creo Flow Analysis. Avec les grandeurs d'écoulement de mélange, les modèles k–ε standard et RNG présentent les mêmes formes générales que dans les modèles de turbulence monophasiques :
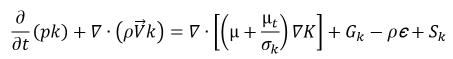
équation 2.84
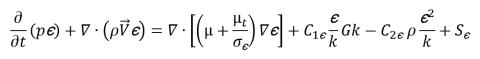
équation 2.85
où la densité du mélange ρ, la vitesse 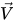 et la viscosité moléculaire μ sont calculées à partir des différentes valeurs de phase en utilisant respectivement les relations de l'équation 2.60, l'équation 2.61 et l'équation 2.63 ; Sk et Sε comprennent à la fois les sources externes et utilisateur et les sources d'interaction de phase. La viscosité turbulente du mélange, μt, est directement calculée à partir de l'expression :
et la viscosité moléculaire μ sont calculées à partir des différentes valeurs de phase en utilisant respectivement les relations de l'équation 2.60, l'équation 2.61 et l'équation 2.63 ; Sk et Sε comprennent à la fois les sources externes et utilisateur et les sources d'interaction de phase. La viscosité turbulente du mélange, μt, est directement calculée à partir de l'expression :
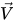 et la viscosité moléculaire μ sont calculées à partir des différentes valeurs de phase en utilisant respectivement les relations de l'équation 2.60, l'équation 2.61 et l'équation 2.63 ; Sk et Sε comprennent à la fois les sources externes et utilisateur et les sources d'interaction de phase. La viscosité turbulente du mélange, μt, est directement calculée à partir de l'expression :
et la viscosité moléculaire μ sont calculées à partir des différentes valeurs de phase en utilisant respectivement les relations de l'équation 2.60, l'équation 2.61 et l'équation 2.63 ; Sk et Sε comprennent à la fois les sources externes et utilisateur et les sources d'interaction de phase. La viscosité turbulente du mélange, μt, est directement calculée à partir de l'expression :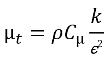
équation 2.86
alors que la production d'énergie cinétique turbulente est calculée en fonction des gradients de vitesse et de viscosité turbulente du mélange :
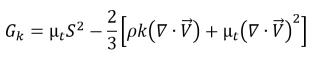
équation 2.87
où S est le module de la vitesse moyenne de déformation du mélange, 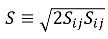
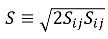
La viscosité turbulente de la phase q peut être calculée comme suit :
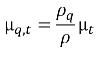
équation 2.87
• Effet d'une diffusion turbulente
Pour les écoulements turbulents multiphases, une force turbulente de dispersion surgit lorsque vous moyennez le terme glissement interfacial instantané, qui agit comme celui de la diffusion de phase. Le modèle à plusieurs fluides eulérien non homogène traite généralement cet effet de turbulence comme une force interphase supplémentaire, déterminée par les gradients des fractions volumiques de phase, dans les équations d'énergie cinétique de phase. Cependant, cet effet de turbulence peut également être modélisé s'il est considéré directement comme un terme de diffusion turbulente dans les équations de fraction volumique de phase. En divisant 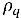 et en groupant toutes les sources comme
et en groupant toutes les sources comme 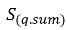 (la somme des transferts de masse interphase et des sources de masse externes), vous obtenez l'équation principale suivante correspondant à la fraction volumique de la phase q dans les écoulements turbulents :
(la somme des transferts de masse interphase et des sources de masse externes), vous obtenez l'équation principale suivante correspondant à la fraction volumique de la phase q dans les écoulements turbulents :
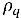 et en groupant toutes les sources comme
et en groupant toutes les sources comme 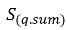 (la somme des transferts de masse interphase et des sources de masse externes), vous obtenez l'équation principale suivante correspondant à la fraction volumique de la phase q dans les écoulements turbulents :
(la somme des transferts de masse interphase et des sources de masse externes), vous obtenez l'équation principale suivante correspondant à la fraction volumique de la phase q dans les écoulements turbulents :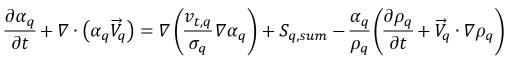
où le premier terme sur la droite est le terme de diffusion turbulente dans la phase q, qui doit respecter la contrainte suivante afin que la conservation de la masse totale soit remplie :
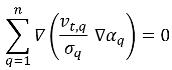
Les termes de diffusion turbulente sont généralement implémentés en tant qu'option. Ils ne sont pas inclus par défaut.
Modélisation des frontières multiphasiques
Dans les modèles multiphases de mélange et VOF, les conditions aux limites des équations d'écoulement et d'énergie sont identiques à celles des écoulements monophases. Celles-ci sont décrites dans les modules Ecoulement (Flow) et Chaleur (Heat). Dans le cas des fractions volumiques de phase, seuls les valeurs fixes et le gradient zéro sont appliqués ci-après :
• Frontière d'entrée n phases
Pour les phases (n–1), les fractions volumiques d'entrée sont prédéterminées, alors que la nième phase est obtenue à l'aide de la contrainte physique :
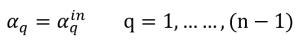
équation 2.88
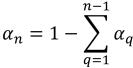
équation 2.89
Et la fraction volumique de chaque phase doit être non négative.
• Frontière de sortie/symétrie/paroi
Dans le cas des phases (n–1), les conditions de gradient zéro s'appliquent pour toutes les frontières de sortie, de symétrie et de paroi, alors que la nième phase est obtenue au moyen de la contrainte physique :
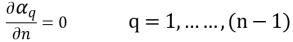
équation 2.90
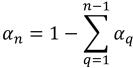
équation 2.91
Les équations principales, les modèles de turbulence et les conditions aux limites ci-dessus constituent le fondement des modèles multiphases de mélange et VOF homogènes. Sans termes sources externes ou utilisateur ni transferts de masse interphase, ils forment un système d'équations fermé et sont résolus numériquement à l'aide d'un solveur multiphase volumes finis basé sur la pression. De nombreuses applications pratiques requièrent des sous-modèles spécifiques tels que la force de tension superficielle dans les modèles VOF et les transferts de masse interphase, pour capturer avec précision les processus et phénomènes correspondants physiques. Plutôt que de réunir les sous-modèles dans les sources externes ou utilisateur, il est recommandé de les inclure directement dans les modèles intégrés.