熱輻射的特性
熱輻射的特性取決於發射體的下列內容:
• 表面溫度
• 表面的平滑度或粗糙度
• 光譜吸收率
• 光譜發射功率
熱輻射是一種電磁波,其由具有一定頻率或波長範圍的連續離散光子能量組成。對於發射體,光譜分佈、波長峰值與所有波長的總輻射量會隨發射體的表面溫度而變化。而在特定的表面溫度下,發射體的吸收率、反射率與發射率皆取決於輻射波長。
輻射能量互換
所有物體皆以光子形式輻射能量,這些光子的移動方向是隨機的,其相位與頻率也是隨機的。當來自一個物體表面的輻射光子到達另一個物體的表面時,如圖 2.35 所示,它們可能會被吸收、反射和/或透射。如果表面上發生輻射入射行為,這種行為可由下列量來描述。
參考資料:R. Siegel and J. R. Howell, "Thermal Radiation Heat Transfer", Hemisphere Publishing Corporation, Washington DC, 1992.
• 吸收比 α - 以特定波長吸收的入射輻射的占比。
• 反射比 ρ - 以特定波長反射的入射輻射的占比。
• 透射比 τ - 以特定波長透射的入射輻射的占比。
這三項係數皆為電磁輻射波波長 λ 的函數。從能量角度考量,三者的總和必須恒等於 1:
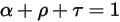
方程式 2.273
根據克希荷夫熱輻射定律,由於互易性,發射體的發射率等於任何特定波長的光譜吸收率:
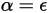
方程式 2.274
其中 ε 是發射率,即在相同溫度與波長下,發射體的輻射能量與完美發射體 (黑體) 的輻射能量之比。
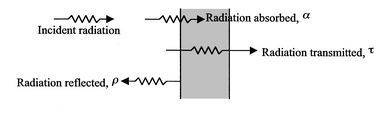
圖 2.35
方程式 2.273 表示,主體對熱輻射的反應行為方式由其吸收比 α、反射比 ρ 與透射比 τ 來表徵。根據 α、ρ,與 τ 的值,定義發射主體的下列理想化類型:
R. Siegel and J. R. Howell, "Thermal Radiation Heat Transfer", Hemisphere Publishing Corporation, Washington DC, 1992
• 不透明體 - 不會透射到達其表面的任何輻射,但可以反射某些輻射。τ=0 且 α+ρ=1
• 透明體 - 會透射到達其表面的所有輻射。τ=1 且 α=ρ=0
• 黑體 - 由普朗克提出的理論模型。黑體是指能夠吸收所有波長的所有入射電磁輻射的物體,而不論頻率或入射角為何。如果輻射發射體在熱力學平衡中符合黑體的物理特性,則此類輻射即稱為黑體輻射。對於黑體,α=ε 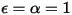 且
且 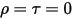
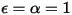 且
且 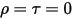
• 白體 - 假設在所有方向上完全且一致地反射所有入射光線。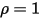 和
和 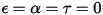
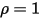 和
和 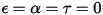
• 灰體 - 其 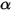 和
和 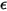 與溫度和波長無關之物體。
與溫度和波長無關之物體。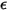 對於所有波長都是一致的。來自灰體或表面的輻射稱為灰體輻射。與灰體輻射不同,一定波譜範圍內的熱輻射稱為非灰體輻射。
對於所有波長都是一致的。來自灰體或表面的輻射稱為灰體輻射。與灰體輻射不同,一定波譜範圍內的熱輻射稱為非灰體輻射。
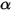 和
和 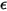 與溫度和波長無關之物體。
與溫度和波長無關之物體。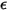 對於所有波長都是一致的。來自灰體或表面的輻射稱為灰體輻射。與灰體輻射不同,一定波譜範圍內的熱輻射稱為非灰體輻射。
對於所有波長都是一致的。來自灰體或表面的輻射稱為灰體輻射。與灰體輻射不同,一定波譜範圍內的熱輻射稱為非灰體輻射。輻射功率
• 功率 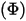 - 特定來源在每單位時間內發射、反射、透射或接收的總體輻射能或淨輻射能。
- 特定來源在每單位時間內發射、反射、透射或接收的總體輻射能或淨輻射能。
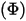 - 特定來源在每單位時間內發射、反射、透射或接收的總體輻射能或淨輻射能。
- 特定來源在每單位時間內發射、反射、透射或接收的總體輻射能或淨輻射能。• 輻照度 (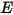 ) - 每單位面積的表面
) - 每單位面積的表面 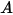 接收的輻射功率。
接收的輻射功率。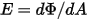
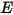 ) - 每單位面積的表面
) - 每單位面積的表面 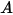 接收的輻射功率。
接收的輻射功率。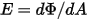
• 發射率 (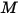 ) - 每單位面積的表面發射的輻射功率
) - 每單位面積的表面發射的輻射功率 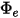 。
。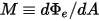
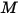 ) - 每單位面積的表面發射的輻射功率
) - 每單位面積的表面發射的輻射功率 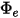 。
。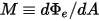
• 強度 (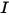 ) - 特定來源在特定方向 (立體角
) - 特定來源在特定方向 (立體角 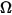 ) 輻射的功率。
) 輻射的功率。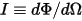
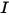 ) - 特定來源在特定方向 (立體角
) - 特定來源在特定方向 (立體角 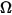 ) 輻射的功率。
) 輻射的功率。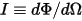
• 輻射度 (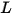 ) - 特定表面在每單位立體角內和每單位投影面積內發射、反射、透射或接收的輻射功率。
) - 特定表面在每單位立體角內和每單位投影面積內發射、反射、透射或接收的輻射功率。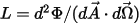
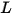 ) - 特定表面在每單位立體角內和每單位投影面積內發射、反射、透射或接收的輻射功率。
) - 特定表面在每單位立體角內和每單位投影面積內發射、反射、透射或接收的輻射功率。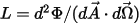
• 普朗克定律
物體在任何溫度下發射的熱輻射都具有很寬的頻率範圍。對於黑體,普朗克定律描述了黑體輻射的頻率分佈,它僅為物體溫度的函數。普朗克定律表明,黑體光譜輻射度 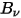 (定義為在每單位頻率
(定義為在每單位頻率 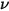 下量測輻射的每單位立體角內,物體每單位面積發射的功率) 的計算公式與主體溫度相關,如下所示:
下量測輻射的每單位立體角內,物體每單位面積發射的功率) 的計算公式與主體溫度相關,如下所示:
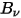 (定義為在每單位頻率
(定義為在每單位頻率 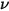 下量測輻射的每單位立體角內,物體每單位面積發射的功率) 的計算公式與主體溫度相關,如下所示:
下量測輻射的每單位立體角內,物體每單位面積發射的功率) 的計算公式與主體溫度相關,如下所示: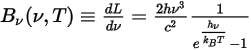
方程式 2.275
其中,
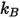 | 波茲曼常數 |
h | 普朗克常數 |
c | 真空或材料媒介中的光速 |
光譜輻射也可使用每單位波長 λ 來表示:
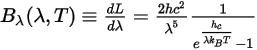
方程式 2.276
• 斯特凡-波茲曼定律:
透過普朗克定律定律對頻率 v 進行積分,由斯特凡-波茲曼定律給出的輻射功率輸出即為黑體發射的輻射功率 (與其溫度有關)。斯特凡-波茲曼定律亦稱為黑體輻射發射率。斯特凡-波茲曼定律表明,黑體表面每單位面積在每單位時間內輻射出的總輻射功率 (涵蓋整個波譜範圍) 與黑體熱力學溫度 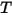 的四次方成正比:
的四次方成正比:
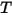 的四次方成正比:
的四次方成正比: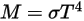
2.277
其中,
σ | 斯特凡-波茲曼常數 |
M | 輻射發射率 |
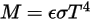
2.278
根據斯特凡-波茲曼定律,物體發射的輻射率與輻射功率可按如下公式計算:
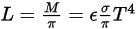
方程式 2.279
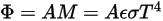
方程式 2.280
• 維恩位移定律
維恩位移定律表明,波長 λ (每單位波長黑體輻射的光譜輻射達到其峰值) 與溫度成反比:
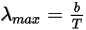
方程式 2.281
其中 b 是維恩位移常數。
模型常數
下表列示了上述理論模型中所用的模型常數:
h | 普朗克常數 | 6.626 069 3(11) ×10 - 34J - s = 4.135 667 43(35) ×10 - 15eV - s |
b | 維恩位移常數 | 2.897 768 5(51) ×10 - 3m - K |
kB | 波茲曼常數 | 1.380 650 5(24) ×10-23J/K = 8.617 343 (15) ×10-5eV/K |
σ | 斯特凡-波茲曼常數 | 5.670 373 (21) ×10-8 W/(m2-K4) |
c | 光速 | 299 792 458 m/s |
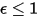 (黑體:
(黑體: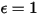 ) 之後,可以將
) 之後,可以將