流体体积 (VOF) 模型的特殊注意事项
VOF 模型与混合模型
在均匀欧拉 多相建模方法中,流体体积 (VOF) 和混合欧拉模型将求解同一个混合 (平均) 控制方程组。但是,它们基于不同的物理机制,从而适用于不同的多相流态:
• 混合模型 - 适用于两相或多相 (流体或颗粒),它们被视为互相贯穿的连续体。它求解的是混合动量方程和能量方程,但不会跟踪相间界面,且从中观察不到清晰的界面。混合模型可应用于低负载的载颗粒流、气泡流、液滴流、沉降和旋风分离器等。此外,也可以将具有预设相对速度的混合模型用于分散相,以对不均匀多相流进行建模。
• VOF 模型 - 通常是瞬态表面跟踪技术,适用于两种或多种不混溶流体,其中相间界面位置备受关注。在 VOF 模型中,所有相共用一个混合动量和能量方程组并进行隐式求解。采用具有更高阶平流方案的精确显式或隐式时间算法来获得相体积分数,以解析相间明锐界面。VOF 模型的典型应用包括分层流动、自由表面流、填充、晃动、液相中大气泡的运动、溃坝后液体的运动、射流断裂的预测 (表面张力) 以及跟踪任何液气界面。
VOF 公式依赖于两种或多种流体 (或相) 没有互相贯穿这一事实。因此,在任何给定的控制体积单元中,局部相体积分数可以单独确定它是仅包含其中一个相还是包含混合相。例如,对于第 q 相,如果某个单元中的体积分数为 αq,则只能有下列三种情况:
◦ αq = 0:该单元中不存在第 q 相
◦ αq = 1:该单元中充满第 q 相
◦ 0< αq < 1:该单元中包含第 q 相与一个或多个其他相之间的界面。
因此,您可以通过求解一个或多个相的体积分数的传输方程来完成相间界面跟踪。
表面张力效应
表面张力是一种尽可能使流体表面积趋于最小的弹力。例如液相中的气泡。在气泡内,由于其邻近气泡的作用而使分子上的净力为零。在液气界面处,由于液体分子间因内聚力产生的吸引力大于空气中分子间因黏附力产生的吸引力,从而形成表面张力。净效应是在其表面形成使气泡收缩的径向内向力。气泡内的压力增加以抵消分子间的吸引力。
• 连续表面力模型
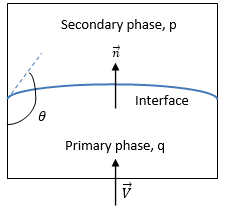
在 Creo Flow Analysis 中,VOF 模型可以包含沿每对相之间的界面的表面张力效应。所采用的表面张力模型基于 Brackbill 等人提出的连续表面力 (CFS) 模型。该方法将表面张力效应视为集中在界面处的附加体积力,而非表面力。对于图 2.26 所示的自由表面界面,主流体为 q 相 (液相),次流体为 p 相 (通常为气相)。利用连续表面力模型,根据界面处表面法线方向的局部梯度计算表面曲率。设 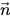 为表面法向矢量,其定义为主流体体积分数 αq 的梯度:
为表面法向矢量,其定义为主流体体积分数 αq 的梯度:
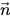 为表面法向矢量,其定义为主流体体积分数 αq 的梯度:
为表面法向矢量,其定义为主流体体积分数 αq 的梯度: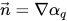
界面曲率 k 是以单位法向矢量的散度定义的:
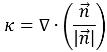
方程 2.93
其中 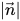 是矢量
是矢量 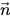 的模。
的模。
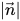 是矢量
是矢量 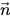 的模。
的模。表面处的表面张力可以使用散度定理表示为体积力,此即添加到混合动量方程中的附加源项:
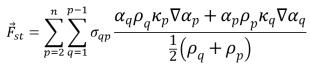
方程 2.94
其中 σqp 是介于流相 q 与流相 p 之间的表面张力系数。其单位为 N/m。方程 2.94 允许将存在两个以上的相的单元附近的力平滑叠加。如果单元中仅存在两个相,您将得到下列关系:
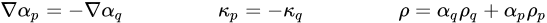
方程 2.95
其中 ρ 是混合密度。然后,将方程 2.94 减少至
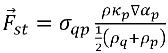
方程 2.96
• 包括表面张力
表面张力效应的重要性由两个无量纲参数确定:雷诺数 Re 和毛管数 Ca,或者雷诺数和韦伯数 We:
如果 Re<<1,则关注的参数为毛管数:
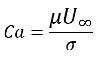
方程 2.97
其中 U∞ 是自由流速度。如果 Ca>>1,由于表面张力过小,可忽略表面张力效应。
如果 Re>>1,则关注的参数为韦伯数:
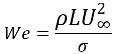
方程 2.98
其中 L 是特征长度。如果 We>>1,当惯性力远远大于表面张力时,表面张力效应也可以忽略不计。
壁面黏附 (接触角)
流体体积 (VOF) 模型具有一个可用于指定壁面黏附角度与表面张力模型的选项。根据 Brackbill 等人提出的模型,不会在壁面上直接应用此边界条件,而是利用界面处流体与壁面之间的接触角来调整近壁面单元中的表面法线。这就是所谓的动态边界条件,可以用来调整近壁面的表面曲率。
如果 θ 为壁面处自由表面界面的接触角,如图 2.26 所示,则近壁面单元处单位法向矢量的计算如下:
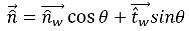
方程 2.99
其中,
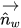 | 垂直于壁的单位矢量 |
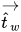 | 相切于壁的单位矢量 |
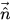 来确定表面的局部曲率 (
来确定表面的局部曲率 (