热辐射的特征
热辐射的特征取决于发射对象或主体的下列属性:
• 表面温度
• 表面的平滑度或粗糙度
• 光谱吸收率
• 光谱发射功率
作为电磁波,热辐射由连续频率或波长的光子能量的连续散射构成。对于发射主体,图谱分布、波长峰值以及所有波长的总辐射量会随发射主体表面温度的不同而变化。反之,在表面温度已给定的位置上,发射主体的吸收率、反射率和辐射率均取决于辐射的波长。
辐射能量的互换
所有主体的辐射能量均为移动方向随机的光子形式,其相位和频率也随机。当辐射光子从一个主体的表面延伸到另一个主体的表面时,如图 2.35 所示,它们可能会被吸收、反射和/或传递。如果表面上发生辐射入射行为,这种行为可通过下列量来描述。
参考:R. Siegel and J. R. Howell, "Thermal Radiation Heat Transfer", Hemisphere Publishing Corporation, Washington DC, 1992.
• 吸收率 α- 在给定波长处吸收的入射辐射分数。
• 反射率 ρ - 在给定波长处反射的入射辐射分数。
• 透射比 τ- 在给定波长处传输的入射辐射分数。
这三个系数是辐射中电磁波长度 λ 的函数。从能量方面考虑,它们相加之和必须等于 1:
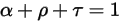
方程 2.273
根据基尔霍夫热辐射定律,发射体的辐射率由于互易性而等于任何特定波长的光谱吸收率:
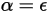
方程 2.274
其中 ε 为辐射率,即在相同温度和波长下,来自发射主体的辐射能与来自完美发射器 (黑体) 的辐射能的比率。
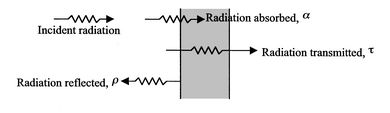
图 2.35
方程 2.273 表明,与热辐射有关的主体反应行为由其吸收率 α、反射率 ρ 和透射率 τ 来表征。根据 α、ρ 和 τ 的值,定义下列理想类型的发射体:
R. Siegel and J. R. Howell, “Thermal Radiation Heat Transfer”, Hemisphere Publishing Corporation, Washington DC, 1992
• 不透明主体 - 不传输任何到达此主体的辐射,但可以反射某些辐射。τ=0 且 α+ρ=1
• 透明主体 - 传输到达此主体的所有辐射。τ=1 且 α=ρ=0
• 黑体 - 普朗克提出的理论模型。黑体是能够吸收所有波长的所有入射电磁辐射的对象,与频率或入射角度无关。如果辐射发射对象在热力学平衡方面满足黑体的物理特征,则辐射称为黑体辐射。对于黑体,α=ε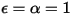 且
且 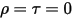
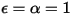 且
且 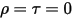
• 白体 - 假设可在所有方向上完全且均匀地反射所有入射光线。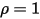 和
和 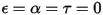
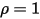 和
和 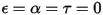
• 灰体 -  和
和 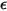 的主体,与温度和波长无关。
的主体,与温度和波长无关。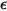 对于所有波长都一致。来自灰体或名为灰色辐射的表面的辐射。与灰体辐射不同,一定波谱范围内的热辐射称为非灰辐射。
对于所有波长都一致。来自灰体或名为灰色辐射的表面的辐射。与灰体辐射不同,一定波谱范围内的热辐射称为非灰辐射。
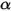 和
和 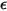 的主体,与温度和波长无关。
的主体,与温度和波长无关。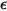 对于所有波长都一致。来自灰体或名为灰色辐射的表面的辐射。与灰体辐射不同,一定波谱范围内的热辐射称为非灰辐射。
对于所有波长都一致。来自灰体或名为灰色辐射的表面的辐射。与灰体辐射不同,一定波谱范围内的热辐射称为非灰辐射。辐射能量
• 能量 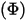 - 给定源每单位时间发出、反射、传输或接收的总辐射能或净辐射能。
- 给定源每单位时间发出、反射、传输或接收的总辐射能或净辐射能。
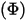 - 给定源每单位时间发出、反射、传输或接收的总辐射能或净辐射能。
- 给定源每单位时间发出、反射、传输或接收的总辐射能或净辐射能。• 辐照度 (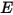 ) - 表面每单位面积接收的辐射能
) - 表面每单位面积接收的辐射能 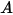 。
。
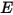 ) - 表面每单位面积接收的辐射能
) - 表面每单位面积接收的辐射能 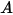 。
。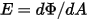
• 发射率 (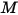 ) - 表面每单位面积发出的辐射能
) - 表面每单位面积发出的辐射能 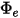 。
。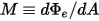
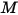 ) - 表面每单位面积发出的辐射能
) - 表面每单位面积发出的辐射能 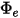 。
。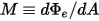
• 强度 (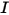 ) - 给定源在给定方向 (立体角,
) - 给定源在给定方向 (立体角,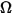 ) 上的辐射能。
) 上的辐射能。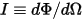
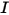 ) - 给定源在给定方向 (立体角,
) - 给定源在给定方向 (立体角,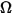 ) 上的辐射能。
) 上的辐射能。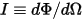
• 辐射率 (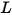 ) - 给定表面上,每单位立体角、每单位投射区域发出、反射、传输或接收的辐射能量。
) - 给定表面上,每单位立体角、每单位投射区域发出、反射、传输或接收的辐射能量。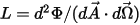
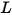 ) - 给定表面上,每单位立体角、每单位投射区域发出、反射、传输或接收的辐射能量。
) - 给定表面上,每单位立体角、每单位投射区域发出、反射、传输或接收的辐射能量。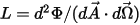
• 普朗克定律
任意温度下主体发出的热辐射均包含很多频率。对于黑体,普朗克定律将黑体辐射的频率分布仅描述为物体温度的函数。普朗克指出,黑体光谱辐射率 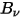 (定义为在每单位频率
(定义为在每单位频率 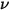 下测量辐射的每单位立体角内,主体每单位面积发射的功率) 的计算公式与主体温度相关,如下所示:
下测量辐射的每单位立体角内,主体每单位面积发射的功率) 的计算公式与主体温度相关,如下所示:
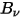 (定义为在每单位频率
(定义为在每单位频率 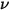 下测量辐射的每单位立体角内,主体每单位面积发射的功率) 的计算公式与主体温度相关,如下所示:
下测量辐射的每单位立体角内,主体每单位面积发射的功率) 的计算公式与主体温度相关,如下所示: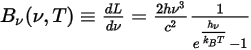
方程 2.275
其中,
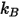 | 玻尔兹曼常数 |
h | 普朗克常数 |
c | 光在真空或物质媒介中的速度 |
光谱辐射也可表示为每单位波长,λ:
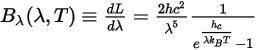
方程 2.276
• 斯蒂芬-玻尔兹曼定律:
通过普朗克定律对频率 v 进行积分,由斯蒂芬-玻尔兹曼定律给出的辐射功率输出即黑体发射的辐射功率 (与其温度有关)。斯蒂芬-玻尔兹曼定律也称为黑体辐射率。斯蒂芬-玻尔兹曼定律规定,黑体表面单位面积在单位时间内辐射出的总辐射功率 (涵盖整个波长范围) 与黑体本身的热力学温度 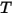 的四次方成正比:
的四次方成正比:
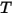 的四次方成正比:
的四次方成正比: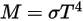
2.277
其中,
σ | 斯蒂芬-玻尔兹曼常数 |
M | 辐射率 |
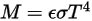
2.278
根据斯蒂芬-玻尔兹曼定律,主体发射的辐射率和辐射功率的计算如下:
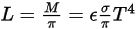
方程 2.279
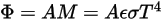
方程 2.280
• 维恩位移定律
维恩位移定律规定,黑体辐射的光谱辐射率在单位波长间隔内达到其峰值时所对应的波长 λ 与温度成反比:
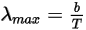
方程 2.281
其中,b 为维恩位移常数。
模型常数
下表给出了以上理论模型中使用的模型常数:
h | 普朗克常数 | 6.626 069 3(11) ×10-34J-s = 4.135 667 43(35) ×10-15eV-s |
b | 维恩位移常数 | 2.897 768 5(51) ×10-3m-K |
kB | 玻尔兹曼常数 | 1.380 650 5(24) ×10-23J/K = 8.617 343 (15) ×10-5eV/K |
σ | 斯蒂芬-玻尔兹曼常数 | 5.670 373 (21) ×10-8 W/(m2-K4) |
c | 光速 | 299 792 458 m/s |
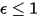 (黑体:
(黑体: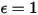 ),
),