Modal Analysis Problems
This chapter contains modal analysis problems and Creo Simulate's results. In a modal analysis, Structure calculates the natural frequencies and mode shapes of your model. Structure also automatically calculates all predefined measures. This list of measures differs based on the analysis type.
This chapter contains the following modal problems:
mvsm001: 2D Plane Strain Shell Cantilever Plate
|
Analysis Type:
|
Modal
|
|
Model Type:
|
2D Plane Strain
|
|
Comparison:
|
Theoretical Results
|
|
Reference:
|
Roark, R.J. and Young, W.C. Formulas for Stress and Strain. NY: McGraw-Hill Book Co. 1982. pp.576578.
|
|
Description:
|
Find the fundamental frequency of a cantilever plate modeled as a plane strain model.
|

Specifications
Element Type: | 2D shell (1) | |
Units: | MKS | |
Dimensions: | width: 2 thickness: 0.01 | |
Material Properties: | Mass Density: 7850 Cost Per Unit Mass: 0 Young's Modulus: 2e11 | Poisson's Ratio: 0.3 Thermal Expansion: 0 Conductivity: 0 |
Constraint: | placed on point A: fixed in all DOF | |
Comparison of Results Data
Theory | Structure | % Difference | |
|---|---|---|---|
Fundamental Frequency (Hz) (mode=1) | 2.1393 | 2.1374 | 0.08% |
Convergence %: 0.4% on Frequency | Max P: 4 | No. Equations: 12 | |
mvsm002: 2D Plane Stress Cantilever Plate
Analysis Type: | Modal |
Model Type: | 2D Plane Stress |
Comparison: | Theoretical Results |
Reference: | Roark, R.J. and Young, W.C. Formulas for Stress and Strain. NY: McGraw-Hill Book Co. 1982. pp.576578. |
Description: | Find the fundamental frequency for the lateral vibration of a cantilever plate. |
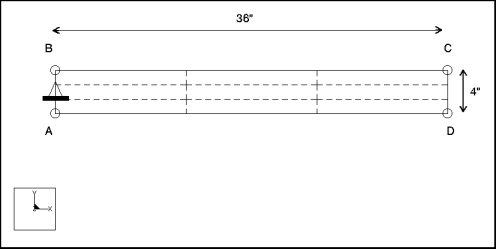
Specifications
Element Type: | 2D plate (1) | |
Units: | IPS | |
Dimensions: | length: 36 width: 4 thickness: 0.1 | |
Material Properties: | Mass Density: 7.28e4 Cost Per Unit Mass: 0 Young's Modulus: 3e7 | Poisson's Ratio: 0.3 Thermal Expansion: 0 Conductivity: 0 |
Constraint: | placed on edge A-B: fixed in TransX and TransY | |
Comparison of Results Data
Theory | Structure | % Difference | |
|---|---|---|---|
Fundamental Frequency (Hz) (mode=1) | 101.326 | 100.988 | 0.33% |
Convergence %: 0.4% on Frequency | Max P: 6 | No. Equations: 42 | |
mvsm003: 2D Plane Strain Solid Cantilever Plate
Analysis Type: | Modal |
Model Type: | 2D Plane Strain |
Comparison: | Theoretical Results |
Reference: | Roark, R.J., and Young, W.C. Formulas for Stress and Strain, NY: McGraw-Hill Book Co. 1982. pp.576578. |
Description: | Find the fundamental frequency of a cantilever plate modeled as a plane strain model. |
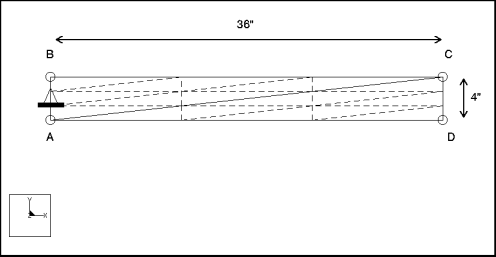
Specifications
Element Type: | 2D solid (2) | |
Units: | IPS | |
Dimensions: | length: 36 width: 4 | |
Material Properties: | Mass Density: 7.28e4 Cost Per Unit Mass: 0 Young's Modulus: 3e7 | Poisson's Ratio: 0.3 Thermal Expansion: 0 Conductivity: 0 |
Constraint: | placed on edge A-B: fixed in TransX, TransY, and RotZ | |
Comparison of Results Data
Theory | Structure | % Difference | |
|---|---|---|---|
Fundamental Frequency (Hz) (mode=1) | 106.219 | 106.604 | 0.36% |
Convergence %: 0.8% on Frequency | Max P: 6 | No. Equations: 42 | |
mvsm004: 2D Axisymmetric Radial Vibration of an Annulus
Analysis Type: | Modal |
Model Type: | 2D Axisymmetric |
Comparison: | ANSYS No. 67 |
Reference: | Timoshenko, S., and Young, D.H. Vibration Problems in Engineering. 3rd ed. NY: D. Van Nostrand Co., Inc. 1955. p. 425, Art. 68. |
Description: | Find the fundamental frequency for the radial vibration of an annulus modeled axisymmetrically. |
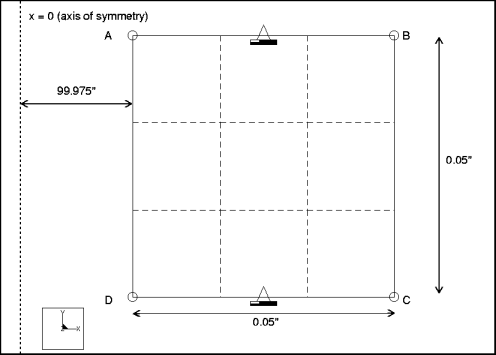
Specifications
Element Type: | 2D solid (1) | |
Units: | IPS | |
Dimensions: | inner radius: 99.975 outer radius: 100.025 height: 0.05 | |
Material Properties: | Mass Density: 7.3e4 Cost Per Unit Mass: 0 Young's Modulus: 3e7 | Poisson's Ratio: 0 Thermal Expansion: 0 Conductivity: 0 |
Constraints: | placed on edge A-B: fixed in TransY and RotZ placed on edge C-D: fixed in TransY and Rot Z | |
Comparison of Results Data
Theory | ANSYS | Structure | % Difference | |
|---|---|---|---|---|
Radial Frequency (Hz) (mode=1) | 322.64 | 322.64 | 322.64 | 0.0% |
Convergence %: 0.0% on Frequency | Max P: 2 | No. Equations: 10 | ||
mvsm005: 3D Radial Vibration of a Ring
Analysis Type: | Modal |
Model Type: | 3D |
Comparison: | Theoretical Results |
Reference: | Love, A.E.H. A Treatise on the Mathematical Theory of Elasticity. 4th ed. NY: Dover Publications. 1944. p. 452, Art. 293b. |
Description: | Determine the first and second modal frequencies for the radial vibration of a ring modeled as a one-quarter model. |
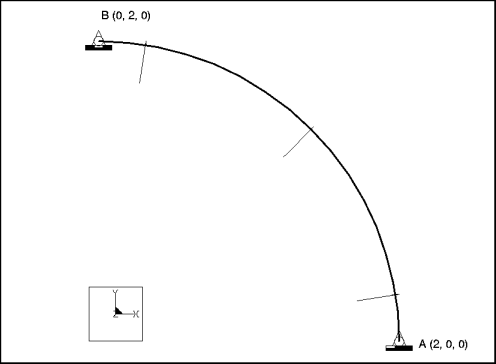
Specifications
Element Type: | beam (1) | |
Units: | IPS | |
Dimensions: | radius: 2 | |
Beam Properties: | Area: 0.01 IYY: 1e3 Shear FY: 0.83333 CY: 1 | J: 1.008e3 IZZ: 8.33e6 Shear FZ: 0.83333 CZ: 1 |
Material Properties: | Mass Density: 7.28e4 Cost Per Unit Mass: 0 Young's Modulus: 3e7 | Poisson's Ratio: 0.3 Thermal Expansion: 0 Conductivity: 0 |
Constraints: | placed on point A: fixed in all DOF except TransX placed on point B: fixed in all DOF except TransY | |
Comparison of Results Data
Theory | Structure | % Difference | |
|---|---|---|---|
Mode 1 Frequency (Hz) | 625.65 | 624.43 | 0.19% |
Mode 2 Frequency (Hz) | 3393.06 | 3369.13 | 0.70% |
Convergence %: 0.0% on Frequency | Max P: 9 | No. Equations: 50 | |
mvsm006: 3D Cantilever Wedge-Shaped Plate
Analysis Type: | Modal |
Model Type: | 3D |
Comparison: | ANSYS No. 62 |
Reference: | Timoshenko, S., and Young, D.H. Vibration Problems in Engineering. 3rd ed. NY: D. Van Nostrand Co., Inc. 1955. p. 392, Art. 62. |
Description: | Find the fundamental frequency for the lateral vibration of a cantilever, wedge-shaped plate. |
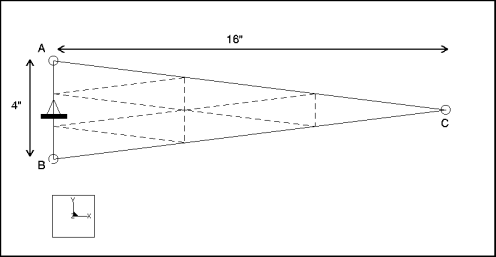
Specifications
Element Type: | shell (1) | |
Units: | IPS | |
Dimensions: | length: 16 width: 4 thickness: 1 | |
Material Properties: | Mass Density: 7.28e4 Cost Per Unit Mass: 0 Young's Modulus: 3e7 | Poisson's Ratio: 0 Thermal Expansion: 0 Conductivity: 0 |
Constraint: | placed on edge A-B: fixed in all DOF | |
Comparison of Results Data
Theory | ANSYS | Structure | % Difference | |
|---|---|---|---|---|
Frequency (Hz) (mode=1) | 259.16 | 260.99 | 259.15 | 0.004% |
Convergence %: 0.0% on Frequency | Max P: 4 | No. Equations: 60 | ||
mvsm007: 3D Cantilever Cylindrical Shell
Analysis Type: | Modal |
Model Type: | 3D |
Comparison: | Theoretical results |
Reference: | Roark, R.J., and Young, W.C. Formula for Stress and Strain. NY: McGraw-Hill Co. 1982. p.576. |
Description: | A cantilever cylindrical shell is modeled as a half cylinder using symmetry. Find the fundamental frequency. |
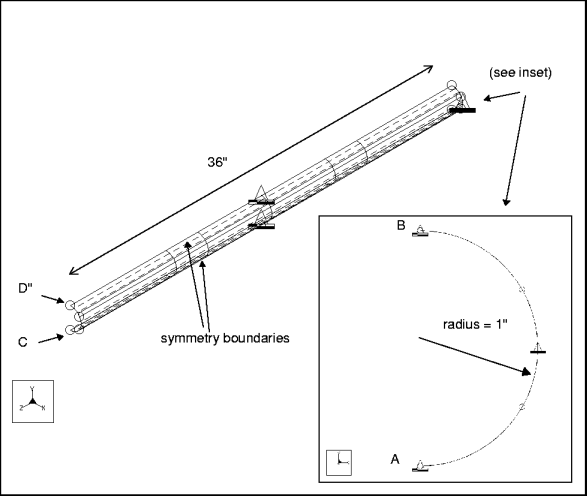
Specifications
Element Type: | shell (3) | |
Units: | IPS | |
Dimensions: | length: 36 radius: 1 thickness: 0.1 | |
Material Properties: | Mass Density: 7.28e4 Cost Per Unit Mass: 0 Young's Modulus: 3e7 | Poisson's Ratio: 0.3 Thermal Expansion: 0 Conductivity: 0 |
Constraint: | placed on edge A-B: fixed in all DOF placed on edge A-C, B-D: fixed in TransX, RotY, and RotZ | |
Comparison of Results Data
Theory | Structure | % Difference | |
|---|---|---|---|
Frequency (Hz) (mode=1) | 62.05 | 62.125 | 0.12% |
Convergence %: 0.4% on Frequency | Max P: 6 | No. Equations: 180 | |
mvsm008: 3D Solid Wedge-Shaped Plate
Analysis Type: | Modal |
Model Type: | 3D |
Comparison: | ANSYS No. 62 |
Reference: | Timoshenko, S., and Young, D.H. Vibration Problems in Engineering. 3rd ed. NY: D. Van Nostrand Co., Inc. 1955. p. 392, Art. 62. |
Description: | Find the fundamental frequency for the lateral vibration of a cantilever, wedge-shaped plate. |
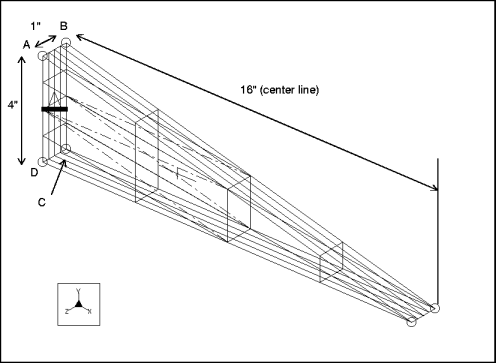
Specifications
Element Type: | solid (1) | |
Units: | IPS | |
Dimensions: | length: 16 width: 4 depth: 1 | |
Material Properties: | Mass Density: 7.28e–4 Cost Per Unit Mass: 0 Young's Modulus: 3e7 | Poisson's Ratio: 0 Thermal Expansion: 0 Conductivity: 0 |
Constraint: | placed on face A-B-C-D: fixed in all DOF | |
Comparison of Results Data
Theory | ANSYS | Structure | % Difference | |
|---|---|---|---|---|
Fundamental Frequency (Hz) (mode=1) | 259.16 | 260.99 | 259.24 | 0.03% |
Convergence %: 0.0% on Frequency | Max P: 4 | No. Equations: 72 | ||
mvsm009: 3D In-Plane Vibration of a Pin-Ended Cross
Analysis Type: | Modal |
Model Type: | 3D |
Reference: | NAFEMS, SBNFA (November 1987), Test 1. |
Description: | Determine the first to eighth modal frequencies for the in-plane vibration of a cross with a pin joint at points A, B, C, & D. |
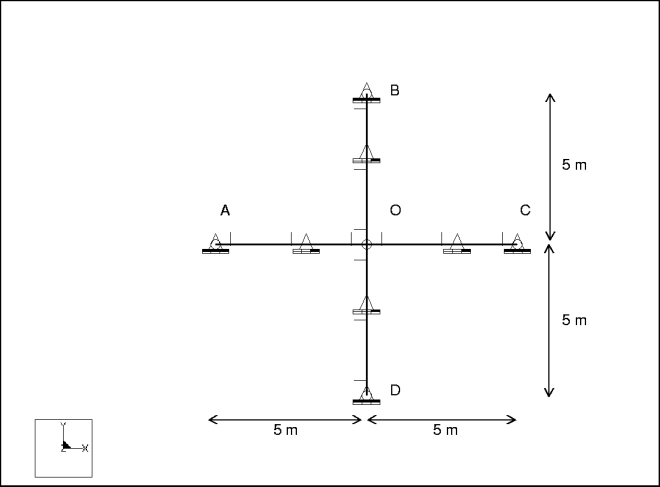
Specifications
Element Type: | beam (4) | |
Units: | NMS | |
Dimensions: | length: 5 | |
Beam Properties: | Area: 0.015625 IYY: 2.0345e–5 Shear FY: 0.83333 CY: 0.0625 | J: 4.069e–5 IZZ: 2.0345e–5 Shear FZ: 0.83333 CZ: 0.0625 |
Material Properties: | Mass Density: 8000 Cost Per Unit Mass: 0 Young's Modulus: 2e11 | Poisson's Ratio: 0.3 Thermal Expansion: 0 Conductivity: 0 |
Constraints: | placed on points A, B, C, D: fixed TransX, TransY, TransZ placed on beams A-O, B-O, C-O, D-O: fixed in TransZ | |
Comparison of Results Data
Theory | Structure | % Difference | |
|---|---|---|---|
Mode 1 Frequency (Hz) | 11.336 | 11.312 | 0.211% |
Mode 2 & 3 Frequency (Hz) | 17.709 | 17.636 | 0.412% |
Mode 4 Frequency (Hz) | 17.709 | 17.636 | 0.412% |
Mode 5 Frequency (Hz) | 45.345 | 45.155 | 0.419% |
Mode 6 & 7 Frequency (Hz) | 57.390 | 56.692 | 1.216% |
Mode 8 Frequency (Hz) | 57.390 | 57.001 | 0.677% |
Convergence %: 3.4% on Frequency | Max P: 8 | No. Equations: 157 | |
mvsm010: 3D Annular Plate Axisymmetric Vibration
Analysis Type: | Modal |
Model Type: | 3D |
Reference: | NAFEMS, SBNFA (November 1987), Test 53. |
Description: | Determine the first to fifth modal frequencies for the axisymmetric vibration of an annular plate. |
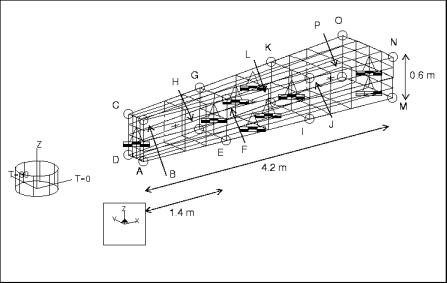
Specifications
Element Type: | solid (3) | |
Units: | NMS | |
Dimensions: | inner radius: 1.8 outer radius: 6 height: 0.6 | |
Material Properties: | Mass Density: 8000 Cost Per Unit Mass: 0 Young's Modulus: 2e11 | Poisson's Ratio: 0.3 Thermal Expansion: 0 Conductivity: 0 |
Constraints: | Location | Degrees of Freedom |
|---|---|---|
constraint1 | placed on surfaces ABCD, BCNO, ADMP, ABMN, CDPO, MNOP | fixed in TransT, RotR, and RotZ |
placed on curve MP | fixed in TransZ |
Comparison of Results Data
Theory | Structure | % Difference | |
|---|---|---|---|
Modal 1 Frequency (Hz) | 18.583 | 18.550 | 0.17% |
Modal 2 Frequency (Hz) | 140.15 | 138.22 | 1.37% |
Modal 3 Frequency (Hz) | 224.16 | 224.16 | 0% |
Modal 4 Frequency (Hz) | 358.29 | 355.80 | 0.7% |
Modal 5 Frequency (Hz) | 629.19 | 620.43 | 1.4% |
Convergence %: 1.3 on Frequency | Max P: 9 | No. Equations: 1094 | |