VOF(유체 부피) 모델의 특별 고려 사항
VOF 모델과 혼합물 모델
균질 Eulerian 다상 모델링 접근 방식에서는 VOF(유체 부피) 모델과 혼합물 오일러 모델 모두 동일한 혼합물(평균) 지배 방정식 세트의 해를 구합니다. 그러나 이러한 모델은 서로 다른 물리적 메커니즘을 기반으로 하며 다음과 같이 서로 다른 다상 흐름 상황에 적용됩니다.
• 혼합물 모델 - 상호 관통하는 연속체로 처리되는 두 개 이상의 위상(유체 또는 미립자)을 위해 설계되었습니다. 이 모델은 혼합물 운동량 방정식 및 에너지 방정식의 해를 구하며, 위상 간 계면이 추적되지 않거나 명확한 계면이 관찰되지 않습니다. 혼합물 모델의 응용에는 저부하, 기포 및 액적 흐름, 침강, 사이클론 분리기에서의 입자 포함 흐름이 포함됩니다. 또한 혼합물 모델을 분산 위상에 대한 지정된 상대 속도와 함께 사용하여 비균질 다상 흐름을 모델링할 수 있습니다.
• VOF 모델 - 일반적으로 위상 간 계면의 위치가 관심 대상인 두 개 이상의 비혼합 유체를 위해 설계된 일시적 표면 추적 기법입니다. VOF 모델에서는 혼합물 운동량 방정식 및 에너지 방정식의 단일 세트가 모든 위상에서 공유되며 암시적으로 해를 구합니다. 위상 부피 분율은 한 쌍의 위상 간 급격한 계면을 해결하기 위해 고차 이송 기법과 함께 정확한 명시적 또는 암시적 시간 알고리즘을 사용하여 구합니다. VOF 모델의 일반적인 응용에는 성층류, 자유 표면 흐름, 충전, 출렁임, 액체 내 큰 기포 운동, 댐 붕괴 후 액체 운동, 제트 분열의 예측(표면 장력), 액체-기체 계면의 추적이 포함됩니다.
VOF 수식은 둘 이상의 유체(또는 위상)가 상호 관통하지 않는다는 사실을 기반으로 합니다. 따라서 제공된 검사 부피 셀에서 국소 위상 부피 분율만으로 해당 셀이 위상 중 하나만 포함할지 아니면 위상의 혼합물을 포함할지를 결정할 수 있습니다. 예를 들어, qth 위상에 대해 셀의 부피 분율이 αq인 경우 다음 세 가지 조건만 가능합니다.
◦ αq = 0: 셀에 qth 위상이 비어 있습니다.
◦ αq = 1: 셀에 qth 위상이 채워져 있습니다.
◦ 0< αq < 1: 셀에 qth 위상과 하나 이상의 다른 위상 간 계면이 포함되어 있습니다.
따라서 하나 이상의 위상 부피 분율에 대한 운송 방정식 솔루션에서 위상 간 계면의 추적을 수행할 수 있습니다.
표면 장력의 효과
표면 장력은 가능한 최소한의 표면 영역을 얻을 수 있도록 하는 유체 표면의 탄성 기질입니다. 액체의 공기 기포를 고려합니다. 기포 내에서 인접 기포로 인한 분자의 알짜 힘은 0입니다. 액체-공기 계면에서 표면 장력은 부착력으로 인한 공기 중 분자 인력보다는 응집력으로 인한 액체 분자의 서로 더 큰 인력에 의해 생성됩니다. 순 효과는 해당 표면에서 방사상 내향력으로, 이러한 힘은 기포를 수축하게 만듭니다. 분자 간 인력의 균형을 잡기 위해 기포 내 압력이 상승합니다.
• 연속체 표면력 모델
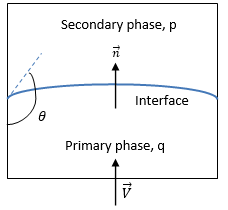
Creo Flow Analysis에서는 VOF 모델에 각 한 쌍의 위상 간 계면과 함께 표면 장력의 효과가 포함될 수 있습니다. 채택된 표면 장력 모델은 Brackbill et al의 연속체 표면력(CFS) 모델을 기반으로 합니다. 이 접근 방식에서는 표면 장력 효과를 표면력보다는 계면에 집중된 추가적인 체적력으로 간주합니다. 그림 2.26에 나와 있는 자유 표면 계면의 경우 일차 유체는 위상 q(액체 위상)이며 이차 유체는 위상 p(일반적으로 기체 위상)입니다. 연속체 표면력 모델에 따라 표면 곡률은 계면에 표면 법선의 국소 구배에서 계산됩니다. 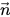 이 일차 유체 부피 분율 αq의 구배로 정의되는 표면 법선 벡터가 되도록 합니다.
이 일차 유체 부피 분율 αq의 구배로 정의되는 표면 법선 벡터가 되도록 합니다.
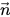 이 일차 유체 부피 분율 αq의 구배로 정의되는 표면 법선 벡터가 되도록 합니다.
이 일차 유체 부피 분율 αq의 구배로 정의되는 표면 법선 벡터가 되도록 합니다.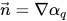
계면 곡률 k는 단위 법선 벡터 발산을 기준으로 정의됩니다.
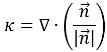
방정식 2.93
여기서 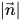 은 벡터
은 벡터 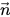 의 크기입니다.
의 크기입니다.
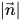 은 벡터
은 벡터 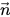 의 크기입니다.
의 크기입니다.표면에서의 표면 장력은 발산 정리를 사용하여 체적력으로 표현되며, 이는 혼합물 운동량 방정식에 추가되는 추가 소스 항입니다.
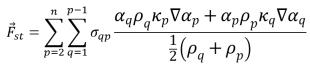
방정식 2.94
여기서 σqp는 유체 q와 유체 p 간의 표면 장력 계수입니다. 이 계수의 단위는 N/m입니다. 방정식 2.94는 위상이 세 개 이상인 셀 근처에 존재하는 힘의 원활한 중첩을 허용합니다. 셀에 위상이 두 개만 있는 경우 다음 관계식을 사용할 수 있습니다.
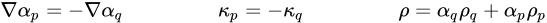
방정식 2.95
여기서 ρ는 혼합물 밀도입니다. 그런 다음 방정식 2.94가 다음과 같이 바뀝니다.
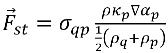
방정식 2.96
• 표면 장력 포함
표면 장력 효과의 중요도는 각 두 개의 비치수 매개 변수인 레이놀즈 수 Re와 모세관 수 Ca 또는 레이놀즈 수와 웨버 수 We에 의해 결정됩니다.
Re<<1이면 관심 대상 매개 변수는 모세관 수입니다.
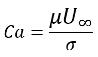
방정식 2.97
여기서 U∞는 자유 기류 속도입니다. Ca>>1이면 표면 장력이 너무 작으므로 표면 장력 효과가 무시됩니다.
Re>>1이면 관심 대상 매개 변수는 웨버 수입니다.
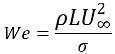
방정식 2.98
여기서 L은 특성 길이입니다. 관성력이 표면 장력보다 휠씬 클 때 We>>1인 경우에도 표면 장력 효과가 무시될 수 있습니다.
벽 부착력(접촉 각도)
VOF(유체 부피) 모델에서 표면 장력 모델과 함께 벽 부착력 각도를 지정하는 옵션을 사용할 수 있습니다. Brackbill et al.에 따라 이 경계 조건을 벽에 직접 적용하는 대신 계면의 유체와 벽 간의 접촉 각도가 벽 근처 셀에서 표면 법선을 조정하는 데 사용됩니다. 동적 경계 조건이라고도 하는 이 조건으로 벽 근처 표면의 곡률이 조정됩니다.
θ가 그림 2.26과 같이 벽에서 자유 표면 계면의 접촉 각도인 경우 벽 근처 셀에서 단위 법선 벡터가 다음으로 계산됩니다.
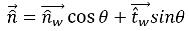
방정식 2.99
여기서 각 항목은 다음을 나타냅니다.
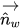 | 벽에 수직인 단위 벡터 |
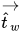 | 벽에 탄젠트인 단위 벡터 |
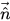 은 표면의 국소 곡률을 결정하고(
은 표면의 국소 곡률을 결정하고(