物理
多成分流れの場合、混合物の速度、圧力、温度、乱流、およびその他の物理量のスカラー輸送方程式を解きます。複数の成分が存在する場合、流体混合物内で成分がどのように輸送されるかを特定する追加の式を解かなければなりません。
複数種 (成分) の説明
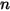 成分流れにおける成分
成分流れにおける成分  の含有量を定量化する、数種類の関連する変数があります。
の含有量を定量化する、数種類の関連する変数があります。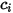 | 成分  のモル濃度 のモル濃度 |
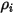 | 成分  の質量濃度 の質量濃度 |
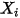 | 成分  のモル分率 のモル分率 |
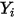 | 成分  の質量分率 の質量分率 |
この 4 つの量は以下のように関連付けられます。
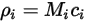
式 2.314
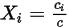
式 2.315
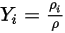
式 2.316
ここで、
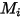 | 成分  の分子量 の分子量 |
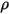 | 混合物密度 |
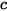 | システム内のすべての成分のモル濃度の合計: |
および
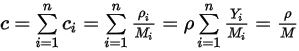
式 2.317
ここで、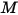 は混合物の分子量です。
は混合物の分子量です。
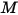 は混合物の分子量です。
は混合物の分子量です。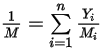
式 2.318
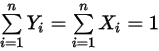
式 2.319
CFA ソルバーで、偏微分輸送方程式を解くことによって、任意の成分 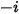 の質量分率
の質量分率 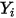 を直接取得します。その他の変数
を直接取得します。その他の変数 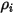 、
、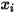 、および
、および 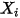 は、ポストプロセスに使用する補助変数です。
は、ポストプロセスに使用する補助変数です。
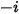 の質量分率
の質量分率 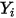 を直接取得します。その他の変数
を直接取得します。その他の変数 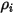 、
、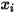 、および
、および 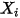 は、ポストプロセスに使用する補助変数です。
は、ポストプロセスに使用する補助変数です。支配方程式
多成分流れでは、混合物のバルク運動は単一の速度、圧力、温度、および乱流フィールドを使用してモデリングされます。化学種の混合と輸送に関して、各成分は質量保存のための独自の支配方程式を持ちます。バルク流れに対する複数成分の影響は、混合物の密度や粘度などの特性のバリエーション、および成分の特性と局所質量分率によって感じられます。
• 質量分率の式
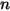 成分混合物流れでは、化学反応がない場合、任意の成分
成分混合物流れでは、化学反応がない場合、任意の成分  の輸送は以下の式によって支配されます。
の輸送は以下の式によって支配されます。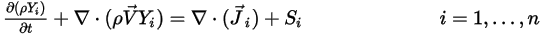
式 2.320
ここで、
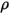 および および 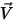 | 混合物の密度と速度 |
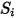 | ユーザー定義の任意のソース |
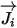 | 質量拡散項 |
層流の場合、速度ベクトル 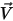 および質量分率
および質量分率 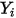 は瞬時変数です。乱流の場合、多成分流れは密度が可変の流れつまり圧縮性流れと見なされるので、これらの速度ベクトルはファーブル平均量です。
は瞬時変数です。乱流の場合、多成分流れは密度が可変の流れつまり圧縮性流れと見なされるので、これらの速度ベクトルはファーブル平均量です。
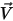 および質量分率
および質量分率 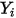 は瞬時変数です。乱流の場合、多成分流れは密度が可変の流れつまり圧縮性流れと見なされるので、これらの速度ベクトルはファーブル平均量です。
は瞬時変数です。乱流の場合、多成分流れは密度が可変の流れつまり圧縮性流れと見なされるので、これらの速度ベクトルはファーブル平均量です。式 2.320で、混合物の量と質量拡散項は以下のように定義されます。
◦ 混合物の密度 - すべての成分の密度を質量で平均した値。
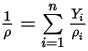
式 2.321
気体種の混合物の場合、混合物の密度は、式 2.318を使用して計算した混合物の分子量 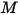 に基づいて、理想気体の法則を使用して計算されます。
に基づいて、理想気体の法則を使用して計算されます。
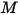 に基づいて、理想気体の法則を使用して計算されます。
に基づいて、理想気体の法則を使用して計算されます。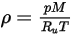
式 2.322
ここで、
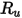 | ユニバーサル気体定数 |
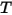 | 混合物の温度 |
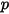 | 絶対圧力 |
動作圧力 (定数) を使用する場合、式 2.322はいわゆる非圧縮性理想気体の法則に書き換えられます。これは種の混合と輸送に適した仮定であり、ここでは通常、動作圧力と比較して、ゲージ圧力は無視できるほどの大きさです。
◦ 混合物の速度 - すべての成分の速度を質量で平均した値。
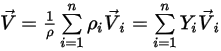
式 2.323
ただし、単一の速度だけを解くので、混合物の速度およびすべての成分の速度の値が同じであると見なします。
◦ 質量拡散流束 - 成分  の質量拡散流束は、層流拡散項と乱流拡散項の 2 つの部分から成り、以下のように表されます。
の質量拡散流束は、層流拡散項と乱流拡散項の 2 つの部分から成り、以下のように表されます。
 の質量拡散流束は、層流拡散項と乱流拡散項の 2 つの部分から成り、以下のように表されます。
の質量拡散流束は、層流拡散項と乱流拡散項の 2 つの部分から成り、以下のように表されます。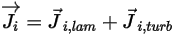
式 2.324
式 2.324で、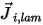 は成分
は成分  の層流拡散流束であり、これは濃度勾配と温度勾配によって生じます。デフォルトでは、Creo Flow Analysis は希釈近似つまりフィックの法則を使用して、濃度勾配による質量拡散をモデリングします。層流拡散流束には以下の式があります。
の層流拡散流束であり、これは濃度勾配と温度勾配によって生じます。デフォルトでは、Creo Flow Analysis は希釈近似つまりフィックの法則を使用して、濃度勾配による質量拡散をモデリングします。層流拡散流束には以下の式があります。
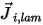 は成分
は成分  の層流拡散流束であり、これは濃度勾配と温度勾配によって生じます。デフォルトでは、Creo Flow Analysis は希釈近似つまりフィックの法則を使用して、濃度勾配による質量拡散をモデリングします。層流拡散流束には以下の式があります。
の層流拡散流束であり、これは濃度勾配と温度勾配によって生じます。デフォルトでは、Creo Flow Analysis は希釈近似つまりフィックの法則を使用して、濃度勾配による質量拡散をモデリングします。層流拡散流束には以下の式があります。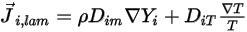
式 2.325
ここで、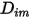 は混合物内の成分
は混合物内の成分  の質量拡散係数、
の質量拡散係数、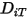 は熱 (ソレー) 拡散係数です。
は熱 (ソレー) 拡散係数です。
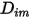 は混合物内の成分
は混合物内の成分  の質量拡散係数、
の質量拡散係数、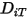 は熱 (ソレー) 拡散係数です。
は熱 (ソレー) 拡散係数です。乱流の場合、式 2.320内の移流をファーブル平均することで導出した変動項が、乱流拡散としてモデリングされます。
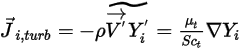
式 2.326
ここで、
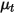 | 乱流粘度 |
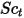 | 乱流シュミット数 デフォルトでは 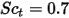 |
乱流拡散の影響は一般には層流拡散の影響よりも甚大です。乱流内の層流拡散の詳細特性の指定の重要性は乱流拡散の詳細特性の指定より低くなります。
混合物流れの質量連続方程式を導出するには、すべての成分の質量分率式を追加して式 2.319を適用します。
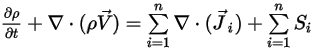
式 2.327
混合物流れの全質量保存を満たすには、すべての成分の拡散項の合計がゼロでなければなりません。
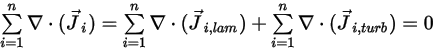
式 2.328
式 2.319および式 2.326から、乱流拡散項は常にゼロになります。したがって、完全な乱流では、通常は式 2.328が自動的に満たされるものと見なします。ただし、層流の場合、または乱流内の層流質量拡散を無視できない場合、式 2.328は以下の形式に書き換えられます。
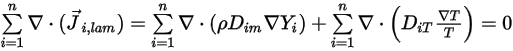
式 2.329
式 2.329を満たすため、2 つの別個の制約を適用します。
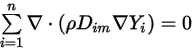
式 2.330
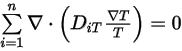
式 2.331
これにより、多成分流れの連続方程式は最終的に以下のようになります。
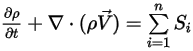
式 2.332
• 拡散係数
◦ 質量拡散係数 - 層流内の質量拡散流束を表す式 2.325は、厳密には、混合物の組成が変化しないか、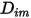 が組成に依存しない場合に有効です。これはキャリアガス以外のすべての成分で
が組成に依存しない場合に有効です。これはキャリアガス以外のすべての成分で 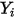 が非常に小さい希釈混合物において許容される近似です。多成分層流内の非希釈混合物については、以下の式から
が非常に小さい希釈混合物において許容される近似です。多成分層流内の非希釈混合物については、以下の式から 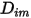 を計算します。
を計算します。
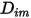 が組成に依存しない場合に有効です。これはキャリアガス以外のすべての成分で
が組成に依存しない場合に有効です。これはキャリアガス以外のすべての成分で 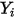 が非常に小さい希釈混合物において許容される近似です。多成分層流内の非希釈混合物については、以下の式から
が非常に小さい希釈混合物において許容される近似です。多成分層流内の非希釈混合物については、以下の式から 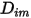 を計算します。
を計算します。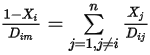
式 2.333
ここで、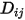 は成分
は成分 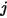 内の成分
内の成分  の 2 成分質量拡散係数であり、これはユーザーが指定または計算する必要があります。
の 2 成分質量拡散係数であり、これはユーザーが指定または計算する必要があります。
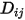 は成分
は成分 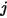 内の成分
内の成分  の 2 成分質量拡散係数であり、これはユーザーが指定または計算する必要があります。
の 2 成分質量拡散係数であり、これはユーザーが指定または計算する必要があります。◦ 指定する値 - 2 成分質量拡散係数 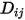 は、定数または温度の関数 (伝熱が考慮される場合) です。この値は直接指定するか、指定されているシュミット数から取得できます。
は、定数または温度の関数 (伝熱が考慮される場合) です。この値は直接指定するか、指定されているシュミット数から取得できます。
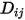 は、定数または温度の関数 (伝熱が考慮される場合) です。この値は直接指定するか、指定されているシュミット数から取得できます。
は、定数または温度の関数 (伝熱が考慮される場合) です。この値は直接指定するか、指定されているシュミット数から取得できます。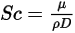
式 2.334
ここで、
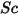 | シュミット数 |
シュミット数は、分子 (質量) 拡散率に対する粘性拡散率の比率として定義されます。
1 つの値または 1 つの温度関数がすべての成分に適用される場合、式 2.333は以下のように書き換えられます
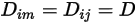
式 2.335
式 2.335は、高濃度のキャリア流体内に低い質量分率で種が存在する希釈混合物のモデリングに適した近似です。そのような場合、定数または温度の関数として 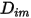 を直接定義します。
を直接定義します。
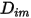 を直接定義します。
を直接定義します。◦ 気体分子運動論 - 理想気体の場合、2 成分質量拡散係数 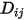 は気体分子運動論を使用して取得することもできます。
は気体分子運動論を使用して取得することもできます。
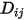 は気体分子運動論を使用して取得することもできます。
は気体分子運動論を使用して取得することもできます。参照: H. A. McGee, "Molecular Engineering", McGraw-Hill, New York, 1991
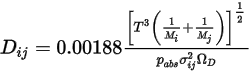
式 2.336
ここで、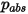 は絶対圧力、
は絶対圧力、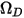 は拡散衝突積分 (システム内の分子の相互作用の測定値) です。
は拡散衝突積分 (システム内の分子の相互作用の測定値) です。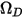 は量
は量 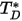 の関数であり、以下のように定義されます。
の関数であり、以下のように定義されます。
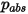 は絶対圧力、
は絶対圧力、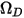 は拡散衝突積分 (システム内の分子の相互作用の測定値) です。
は拡散衝突積分 (システム内の分子の相互作用の測定値) です。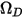 は量
は量 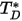 の関数であり、以下のように定義されます。
の関数であり、以下のように定義されます。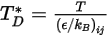
式 2.337
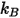 はボルツマン定数であり、これはユニバーサル気体定数
はボルツマン定数であり、これはユニバーサル気体定数 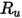 をアボガドロ数で割った値として定義されます。混合物の
をアボガドロ数で割った値として定義されます。混合物の 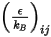 はジオメトリ平均です。
はジオメトリ平均です。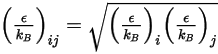
式 2.338
2 成分混合物の場合、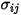 は個々の
は個々の 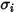 および
および 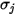 の算術平均として計算されます。
の算術平均として計算されます。
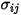 は個々の
は個々の 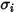 および
および 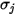 の算術平均として計算されます。
の算術平均として計算されます。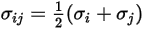
式 2.339
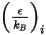 および
および 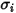 は混合物内の成分
は混合物内の成分  の Lennard-Jones パラメータです。具体的には、
の Lennard-Jones パラメータです。具体的には、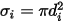 は直径
は直径 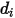 の球体分子の衝突 2 次元断面であり (衝突先の分子にも直径
の球体分子の衝突 2 次元断面であり (衝突先の分子にも直径 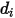 があるので、分子はその直径の 2 倍の領域をスイープします)、
があるので、分子はその直径の 2 倍の領域をスイープします)、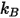 =1.38064852(79) ×10-23(J/K) はボルツマン定数です。
=1.38064852(79) ×10-23(J/K) はボルツマン定数です。Creo Flow Analysis では、直径 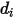 およびエネルギー
およびエネルギー 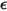 を指定して 2 つの Lennard-Jones パラメータを求めます。
を指定して 2 つの Lennard-Jones パラメータを求めます。
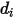 およびエネルギー
およびエネルギー 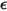 を指定して 2 つの Lennard-Jones パラメータを求めます。
を指定して 2 つの Lennard-Jones パラメータを求めます。◦ 熱拡散係数 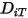 - 熱拡散係数は、定数、温度の多項式関数、ユーザー定義関数として、または以下によって計算される、経験に基づいた組成依存の式を使用して定義できます。
- 熱拡散係数は、定数、温度の多項式関数、ユーザー定義関数として、または以下によって計算される、経験に基づいた組成依存の式を使用して定義できます。
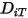 - 熱拡散係数は、定数、温度の多項式関数、ユーザー定義関数として、または以下によって計算される、経験に基づいた組成依存の式を使用して定義できます。
- 熱拡散係数は、定数、温度の多項式関数、ユーザー定義関数として、または以下によって計算される、経験に基づいた組成依存の式を使用して定義できます。参照: K. K. Y. Kuo, "Principles of Combustion", John Wiley and Sons, New York, 1986
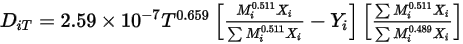
式 2.340
この形式の熱拡散係数によって、熱せられたサーフェスへの重い分子の拡散速度は遅く、軽い分子の拡散速度は速くなります。
• 運動量方程式
質量で重み付けされた特性と速度を使用すると、すべての成分から成る混合物の運動量方程式は、以下に示す単一の流体流れの運動量方程式と同じになります。
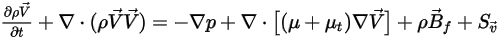
式 2.341
ここで、混合物の密度と速度は式 2.321、式 2.322、および式 2.323を使用して計算されます。乱流粘度は混合物流れに基づいた乱流モデルから直接計算されるので、その値は成分には依存しません。層流粘度は以下のように計算されます。
◦ 質量平均層流粘度 - 非理想気体混合物の場合、混合物の粘度は純粋な化学種 (成分) の粘度の質量分率平均に基づいて計算されます。
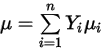
式 2.342
◦ 気体分子運動論 - 理想気体混合物の場合、混合物の粘度は気体分子運動論に基づいて計算されます。各成分の動粘度はボルツマン方程式に基づきます。
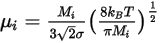
式 2.343
質量拡散では、混合物内の気体成分の粘度を計算するには Lennard-Jones パラメータ 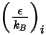 および
および 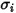 が必要です。
が必要です。
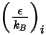 および
および 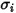 が必要です。
が必要です。理想気体混合物の粘度は以下のように計算されます。
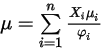
式 2.344
ここで、
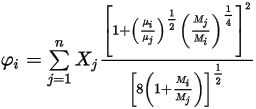
式 2.345
• エネルギー方程式
熱モジュールで説明したように、すべての成分から成る混合物のエネルギー方程式は以下のように表されます。
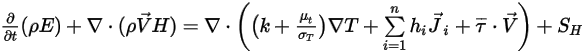
式 2.346
ここで、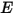 および
および 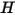 は
は 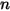 成分混合物の総内部エネルギーおよび総エンタルピーです。さらに、混合物の比熱
成分混合物の総内部エネルギーおよび総エンタルピーです。さらに、混合物の比熱 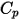 および静的エンタルピー
および静的エンタルピー 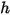 は、以下に示すように各成分の該当する値を質量平均することによって取得されます。
は、以下に示すように各成分の該当する値を質量平均することによって取得されます。
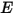 および
および 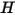 は
は 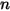 成分混合物の総内部エネルギーおよび総エンタルピーです。さらに、混合物の比熱
成分混合物の総内部エネルギーおよび総エンタルピーです。さらに、混合物の比熱 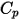 および静的エンタルピー
および静的エンタルピー 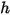 は、以下に示すように各成分の該当する値を質量平均することによって取得されます。
は、以下に示すように各成分の該当する値を質量平均することによって取得されます。◦ 混合物の質量平均の熱容量
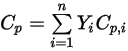
式 2.347
◦ 質量平均の混合物のエネルギーとエンタルピー
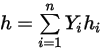
式 2.348
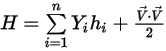
式 2.349
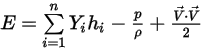
式 2.350
成分の静的エンタルピーは、標準状態の基準エンタルピーと顕エンタルピーの 2 つの部分から成ります。多成分フローでは、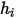 を計算する際にエンタルピーの両方の部分 (絶対値つまり合計値) を含めます。
を計算する際にエンタルピーの両方の部分 (絶対値つまり合計値) を含めます。
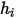 を計算する際にエンタルピーの両方の部分 (絶対値つまり合計値) を含めます。
を計算する際にエンタルピーの両方の部分 (絶対値つまり合計値) を含めます。式 2.336において、右辺の第 1 項はエネルギーの拡散を表します。これは、熱伝導、種の拡散によるエネルギー輸送、および粘性加熱の 3 つの部分から成ります。混合物の熱伝導は、単一流体流れにおける場合と同じ方法でモデリングされます。Creo Flow Analysis で、混合物の熱伝導率は以下のように計算されます。
◦ 質量平均熱伝導率 - 非理想気体混合物の場合、混合物の熱伝導率は純粋な種 (成分) の熱伝導率の単純な質量分率平均に基づいて計算されます。
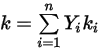
式 2.351
これは Creo Flow Analysis でのデフォルトの方法です。
◦ 気体分子運動論 - 理想気体混合物の場合、混合物の熱伝導率は気体分子運動論に基づいて計算できます。各成分の熱伝導率は以下の形式をとります。
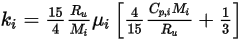
式 2.352
ここで、
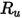 | ユニバーサル気体定数 |
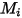 | 分子量 |
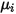 | 成分の指定または計算された粘度 |
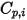 | 成分の指定または計算された比熱容量 |
層流粘度 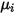 と同様に、比熱
と同様に、比熱 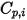 も気体分子運動論を使用して取得できます。
も気体分子運動論を使用して取得できます。
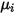 と同様に、比熱
と同様に、比熱 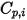 も気体分子運動論を使用して取得できます。
も気体分子運動論を使用して取得できます。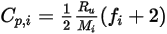
式 2.353
ここで、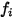 は気体成分
は気体成分  のエネルギー貯蔵のモード数 (自由度) です。
のエネルギー貯蔵のモード数 (自由度) です。
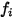 は気体成分
は気体成分  のエネルギー貯蔵のモード数 (自由度) です。
のエネルギー貯蔵のモード数 (自由度) です。理想気体混合物の熱伝導率は以下のように計算されます。
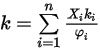
式 2.354
ここで、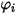 は式 2.335によって表されます。
は式 2.335によって表されます。
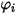 は式 2.335によって表されます。
は式 2.335によって表されます。2 つ目の拡散項、
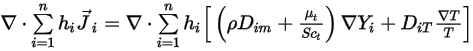
式 2.355
は、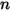 成分流れにおける化学種の拡散によるエンタルピーの輸送を表します。この項はエンタルピーフィールドに非常に大きな影響を与えることがあるので、無視してはなりません。ルイス数では、質量拡散率
成分流れにおける化学種の拡散によるエンタルピーの輸送を表します。この項はエンタルピーフィールドに非常に大きな影響を与えることがあるので、無視してはなりません。ルイス数では、質量拡散率 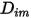 に対する熱拡散率
に対する熱拡散率 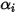 の比率:
の比率:
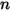 成分流れにおける化学種の拡散によるエンタルピーの輸送を表します。この項はエンタルピーフィールドに非常に大きな影響を与えることがあるので、無視してはなりません。ルイス数では、質量拡散率
成分流れにおける化学種の拡散によるエンタルピーの輸送を表します。この項はエンタルピーフィールドに非常に大きな影響を与えることがあるので、無視してはなりません。ルイス数では、質量拡散率 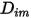 に対する熱拡散率
に対する熱拡散率 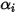 の比率:
の比率: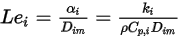
式 2.356
がどの種でも 1 でない場合、この項を無視すると大きな誤差が生じる可能性があります。
3 つ目の拡散項は粘性加熱寄与 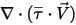 です。これは単一流体流れにおける場合と同じ方法で扱われますが、混合物の層流粘度と乱流粘度を使用してせん断応力
です。これは単一流体流れにおける場合と同じ方法で扱われますが、混合物の層流粘度と乱流粘度を使用してせん断応力 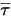 を計算します。一般ソース項
を計算します。一般ソース項 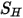 はすべての成分での外部熱ソースまたはユーザー熱ソースの合計です。
はすべての成分での外部熱ソースまたはユーザー熱ソースの合計です。
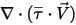 です。これは単一流体流れにおける場合と同じ方法で扱われますが、混合物の層流粘度と乱流粘度を使用してせん断応力
です。これは単一流体流れにおける場合と同じ方法で扱われますが、混合物の層流粘度と乱流粘度を使用してせん断応力 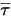 を計算します。一般ソース項
を計算します。一般ソース項 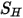 はすべての成分での外部熱ソースまたはユーザー熱ソースの合計です。
はすべての成分での外部熱ソースまたはユーザー熱ソースの合計です。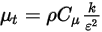
式 2.357
さらに、乱流運動エネルギーの生成は混合物の乱流粘度と速度勾配に基づいて計算されます。
多成分境界のモデリング
多成分流れにおける、流れ、エネルギー、乱流モデリングの式の境界条件は、流れモジュール、熱モジュール、および乱流モジュールで説明されている単相流れでの境界条件と同じです。成分の質量分率の境界条件は、指定された値、指定された積流束、勾配、またはそのすべてから成ります。
• n 成分入口境界
入口境界では、成分の正味の輸送は熱伝達と拡散の両方の寄与から成ります。熱伝達は、指定されている入口において種の質量分率によって決まります。拡散は、計算された質量分率フィールドの勾配に依存します。入口の対流速度が非常に遅い場合、拡散によって入口で多くの質量を得たり失ったりすることがあります。このため、入口での拡散はデフォルトでは含まれていませんが、オプションとして有効にできます。

式 2.358
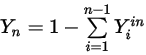
式 2.359
さらに、各成分の質量分率は負でない値でなければなりません。
◦ 指定された容積流束 - 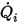 が成分
が成分  に事前に指定されている入口容積流束であるとした場合、入口における各成分の質量流束
に事前に指定されている入口容積流束であるとした場合、入口における各成分の質量流束 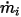 および総質量流束
および総質量流束 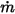 は以下のようになります。
は以下のようになります。
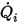 が成分
が成分  に事前に指定されている入口容積流束であるとした場合、入口における各成分の質量流束
に事前に指定されている入口容積流束であるとした場合、入口における各成分の質量流束 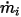 および総質量流束
および総質量流束 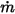 は以下のようになります。
は以下のようになります。
式 2.360
ここで、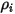 は成分
は成分  の入口密度です。
の入口密度です。
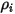 は成分
は成分  の入口密度です。
の入口密度です。定義により、質量分率は以下のように計算されます。
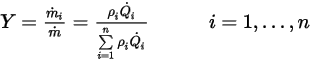
式 2.361
◦ 出口境界、対称境界、壁境界 - 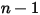 成分では、すべての出口境界、対称境界、壁境界にゼロ勾配条件が適用されるのに対し、
成分では、すべての出口境界、対称境界、壁境界にゼロ勾配条件が適用されるのに対し、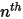 相は物理的な制約を使用して取得します。
相は物理的な制約を使用して取得します。
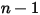 成分では、すべての出口境界、対称境界、壁境界にゼロ勾配条件が適用されるのに対し、
成分では、すべての出口境界、対称境界、壁境界にゼロ勾配条件が適用されるのに対し、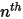 相は物理的な制約を使用して取得します。
相は物理的な制約を使用して取得します。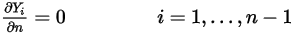
式 2.362
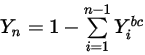
式 2.363
ここで、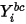 は式 2.347から取得された境界値です。
は式 2.347から取得された境界値です。
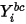 は式 2.347から取得された境界値です。
は式 2.347から取得された境界値です。数値に関する考慮事項
上記の支配方程式、乱流モデル、および境界条件は、多成分混合モデルの基礎となります。外部またはユーザーソース項および化学反応がない場合、これらは閉じた連立方程式となり、圧力に基づいた有限体積ソルバーを使用して数値解を得ます。
質量分率輸送方程式はすべての成分について計算されます。物理的な制約を満たすため、実際の質量分率はすべての成分で計算された値の合計によって調整されます。

式 2.364
ここで、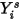 は式 2.320を解くことによって取得された値です。実際の質量分率は以下のようになります。
は式 2.320を解くことによって取得された値です。実際の質量分率は以下のようになります。
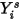 は式 2.320を解くことによって取得された値です。実際の質量分率は以下のようになります。
は式 2.320を解くことによって取得された値です。実際の質量分率は以下のようになります。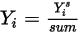
式 2.365
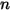 成分から成る混合物に適用されることを示しています。
成分から成る混合物に適用されることを示しています。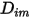 および熱拡散係数
および熱拡散係数 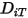 が必要です。
が必要です。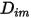 および
および 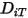 を求める方法は以下のとおりです。
を求める方法は以下のとおりです。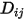 が指定されている非希釈混合物の場合、
が指定されている非希釈混合物の場合、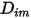 を計算します。
を計算します。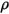 、分子粘度を
、分子粘度を 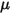 、速度を
、速度を 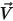 とした場合、
とした場合、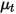 は以下の式から直接計算されます。
は以下の式から直接計算されます。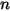 成分流れでは、入口の質量分率は
成分流れでは、入口の質量分率は 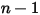 成分に事前に指定されているのに対し、
成分に事前に指定されているのに対し、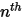 成分の質量分率は物理的な制約の
成分の質量分率は物理的な制約の