Modellazione del trasferimento termico radiativo
In un sistema di fluidi termici, le superfici solide, il flusso del fluido o entrambi possono essere soggetti a riscaldamento o raffreddamento a causa della radiazione. Nei modelli CFA, il trasferimento termico radiativo si spiega risolvendo l'equazione del trasferimento radiativo (RTE) e successivamente ottenendo il termine di origine radiativa per l'equazione di conservazione dell'energia totale. Il modello di radiazione superficie a superficie (S2S) è un approccio alla modellazione ampiamente utilizzato ed è il modello scelto in Creo Flow Analysis.
Equazione del trasferimento radiativo
Quando un raggio di radiazione attraversa uno strato di un mezzo assorbente, emittente e disperdente in una determinata direzione, perde energia attraverso sia l'assorbimento che la dispersione. Il raggio inoltre acquisisce energia dalle fonti di luce presenti nel mezzo attraverso l'emissione e la dispersione direzionata verso il raggio. Il bilancio energetico complessivo del raggio su uno strato non finito del mezzo comporta un'equazione differenziale, nota come equazione del trasferimento radiativo (RTE).
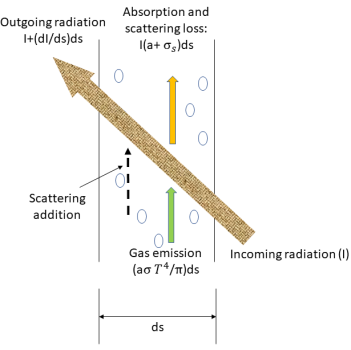
Per derivare l'equazione del trasferimento radiativo, occorre considerare che un raggio di radiazione entrante con intensità I viaggia attraverso un mezzo, ad esempio un gas, con lo spessore incrementale ds nella direzione di 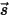 , come mostrato nella figura. Attraverso lo strato del mezzo, l'incidenza in corrispondenza della posizione
, come mostrato nella figura. Attraverso lo strato del mezzo, l'incidenza in corrispondenza della posizione 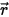 ⃗ e la direzione
⃗ e la direzione 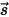 cambiano in quattro modi, agendo in modo da aumentare (energia acquisita +) o diminuire (energia persa -) l'intensità della radiazione
cambiano in quattro modi, agendo in modo da aumentare (energia acquisita +) o diminuire (energia persa -) l'intensità della radiazione 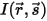 :
:
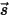 , come mostrato nella figura. Attraverso lo strato del mezzo, l'incidenza in corrispondenza della posizione
, come mostrato nella figura. Attraverso lo strato del mezzo, l'incidenza in corrispondenza della posizione 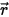 ⃗ e la direzione
⃗ e la direzione 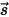 cambiano in quattro modi, agendo in modo da aumentare (energia acquisita +) o diminuire (energia persa -) l'intensità della radiazione
cambiano in quattro modi, agendo in modo da aumentare (energia acquisita +) o diminuire (energia persa -) l'intensità della radiazione 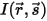 :
:• Assorbimento - Un mezzo, ad esempio un gas, assorbe una frazione della radiazione che lo attraversa. Con il coefficiente di assorbimento 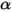 , l'energia della radiazione persa attraverso l'assorbimento è:
, l'energia della radiazione persa attraverso l'assorbimento è:
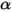 , l'energia della radiazione persa attraverso l'assorbimento è:
, l'energia della radiazione persa attraverso l'assorbimento è: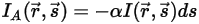
equazione 2.282
• Dispersione - Un mezzo, ad esempio un gas, disperde una frazione dell'energia di radiazione in un'altra direzione (lontano dalla direzione 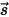 ) quando il raggio attraversa il mezzo. Con il coefficiente di dispersione
) quando il raggio attraversa il mezzo. Con il coefficiente di dispersione 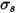 , l'energia di radiazione persa attraverso la dispersione è:
, l'energia di radiazione persa attraverso la dispersione è:
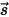 ) quando il raggio attraversa il mezzo. Con il coefficiente di dispersione
) quando il raggio attraversa il mezzo. Con il coefficiente di dispersione 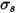 , l'energia di radiazione persa attraverso la dispersione è:
, l'energia di radiazione persa attraverso la dispersione è: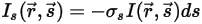
Equazione 2.283
• Emissione - Un mezzo emette energia di radiazione verso il raggio come un corpo grigio in base alla temperatura locale (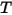 ) e alle caratteristiche di emissione. In base alla legge di Stefan-Boltzmann e alla reciprocità tra emissione e assorbimento, equazione 2.274 ed equazione 2.279, la radianza emessa dal mezzo è
) e alle caratteristiche di emissione. In base alla legge di Stefan-Boltzmann e alla reciprocità tra emissione e assorbimento, equazione 2.274 ed equazione 2.279, la radianza emessa dal mezzo è 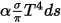 .
.
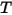 ) e alle caratteristiche di emissione. In base alla legge di Stefan-Boltzmann e alla reciprocità tra emissione e assorbimento, equazione 2.274 ed equazione 2.279, la radianza emessa dal mezzo è
) e alle caratteristiche di emissione. In base alla legge di Stefan-Boltzmann e alla reciprocità tra emissione e assorbimento, equazione 2.274 ed equazione 2.279, la radianza emessa dal mezzo è 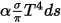 .
.Inoltre, se si suppone che n sia l'indice di rifrazione del mezzo (definito come rapporto tra velocità della luce nel vuoto e relativa velocità nel mezzo specificato), l'energia effettiva ottenuta dal raggio di radiazione è:
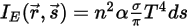
Equazione 2.284
• Dispersione di altra radiazione - Una frazione di altre fonti di radiazione nello strato del mezzo viene dispersa nel raggio di radiazione a seconda dei vettori di posizione e direzione 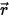 e
e 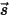 . Se si introduce
. Se si introduce 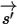
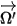 per rappresentare la direzione e l'angolo solido del fascio di radiazione e
per rappresentare la direzione e l'angolo solido del fascio di radiazione e 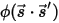 come funzione di fase, la frazione di intensità di un raggio che viaggia in tutte le direzioni viene dispersa nella direzione di
come funzione di fase, la frazione di intensità di un raggio che viaggia in tutte le direzioni viene dispersa nella direzione di 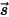 ⃗ come:
⃗ come:
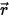 e
e 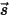 . Se si introduce
. Se si introduce 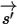
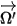 per rappresentare la direzione e l'angolo solido del fascio di radiazione e
per rappresentare la direzione e l'angolo solido del fascio di radiazione e 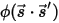 come funzione di fase, la frazione di intensità di un raggio che viaggia in tutte le direzioni viene dispersa nella direzione di
come funzione di fase, la frazione di intensità di un raggio che viaggia in tutte le direzioni viene dispersa nella direzione di 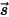 ⃗ come:
⃗ come: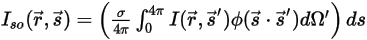
equazione 2.285
Nell'equazione 2.285, i processi di dispersione vengono ignorati.
Con la radiazione entrante 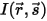 e la radiazione uscente
e la radiazione uscente 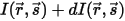 , il bilancio energetico radiativo nella direzione
, il bilancio energetico radiativo nella direzione 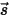 ⃗ presenta la forma seguente:
⃗ presenta la forma seguente:
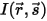 e la radiazione uscente
e la radiazione uscente 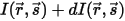 , il bilancio energetico radiativo nella direzione
, il bilancio energetico radiativo nella direzione 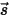 ⃗ presenta la forma seguente:
⃗ presenta la forma seguente: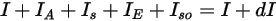
equazione 2.286
Sostituendo l'equazione 2.282 con l'equazione 2.285 nell'equazione 2.286 e dividendola per 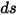 , il risultato è l'equazione del trasferimento radiativo (RTE) seguente:
, il risultato è l'equazione del trasferimento radiativo (RTE) seguente:
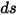 , il risultato è l'equazione del trasferimento radiativo (RTE) seguente:
, il risultato è l'equazione del trasferimento radiativo (RTE) seguente: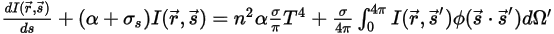
equazione 2.287
La RTE è un'equazione integro-differenziale del primo ordine per l'intensità di radiazione 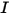 in una direzione fissa
in una direzione fissa 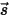 . Per risolvere questa equazione all'interno di un dominio, è necessario utilizzare il campo temperatura all'interno del dominio, le condizioni al limite per
. Per risolvere questa equazione all'interno di un dominio, è necessario utilizzare il campo temperatura all'interno del dominio, le condizioni al limite per 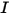 su entrambe le superfici, interna ed esterna, nonché le interfacce tra due mezzi diversi.
su entrambe le superfici, interna ed esterna, nonché le interfacce tra due mezzi diversi.
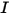 in una direzione fissa
in una direzione fissa 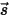 . Per risolvere questa equazione all'interno di un dominio, è necessario utilizzare il campo temperatura all'interno del dominio, le condizioni al limite per
. Per risolvere questa equazione all'interno di un dominio, è necessario utilizzare il campo temperatura all'interno del dominio, le condizioni al limite per 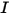 su entrambe le superfici, interna ed esterna, nonché le interfacce tra due mezzi diversi.
su entrambe le superfici, interna ed esterna, nonché le interfacce tra due mezzi diversi.La temperatura media locale si ottiene risolvendo l'equazione di conservazione dell'energia totale (comprese le fonti radiative), descritta nel modulo Calore (Heat). Per la radiazione termica, tuttavia, il trattamento del limite è complesso e dipende dai modelli di radiazione. In generale, un limite può essere un mezzo opaco che emette, riflette e assorbe o un mezzo semi-trasparente che è anche in grado di trasmettere. Inoltre, la riflessione e la trasmissione possono essere diffuse o speculari oppure sia diffuse che speculari. Ad esempio, su un limite opaco emittente e riflettente con radiazione di corpo grigio e, a seconda del tipo di riflessione, l'intensità di un raggio può essere espressa come segue:
◦ Limite opaco con emissione e riflessione diffuse:
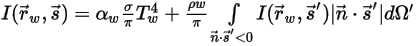
Equazione 2.288
◦ Limite opaco con emissione diffusa e riflessione speculare:
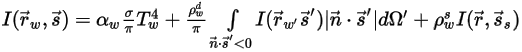
Equazione 2.289
dove
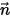 ⃗ ⃗ | vettore unitario normale a superficie alla posizione 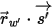 |
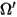 | direzione e angolo solido di un raggio riflesso in modo diffuso (riflessione uniforme in tutte le direzioni) |
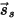 | direzione del raggio riflesso in modo speculare (riflessione perfetta a seconda dell'incidenza) |
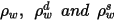 | riflettività della superficie, riflettività diffusa e riflettività speculare, rispettivamente, che hanno la seguente relazione: 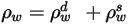 equazione 2.290 |
Con le condizioni al limite specificate, l'equazione 2.287 regola il trasferimento dell'intensità della radiazione in una direzione specificata. Per le radiazioni di corpi grigi, l'equazione 2.287 deve essere risolta in tutte le direzioni all'interno di una sfera. Per le radiazioni di corpi non grigi, l'intensità dipende anche dalle lunghezze d'onda. Pertanto, l'equazione deve essere risolta in tutte le direzioni nell'intero spettro delle lunghezze d'onda. La soluzione diretta dell'equazione del trasferimento radiativo richiede naturalmente molto tempo. In molte simulazioni ingegneristiche è pertanto auspicabile utilizzare modelli in qualche modo semplificati ma approssimati per tenere conto delle dipendenze direzionali e spettrali. Nelle simulazioni di CFD vengono adottati abitualmente i modelli di radiazione riportati di seguito, di cui è possibile trovare la descrizione dettagliata nei riferimenti.
Riferimenti: R. Siegel and J. R. Howell, "Thermal Radiation Heat Transfer", Hemisphere Publishing Corporation, Washington DC, 1992.
▪ Modello di radiazione di Rosseland
Riferimenti: R, Siegel and J. R. Howell, "Thermal Radiation Heat Transfer", Hemisphere Publishing Corporation, Washington DC, 1992.
▪ Modello di radiazione P-1
Riferimenti: R. Siegel and J. R. Howell, "Thermal Radiation Heat Transfer", Hemisphere Publishing Corporation, Washington DC, 1992.
▪ Modello di radiazione con trasferimento distinto
Riferimenti: N. G. Shah, "A New Method of Computation of Radiant Heat Transfer in Combustion Chambers", PhD thesis, Imperial College of Science and Technology, London, England, 1979.
Riferimenti: M. G. Carvalho, T. Farias, and P. Fontes, "Predicting Radiative Heat Transfer in Absorbing, Emitting, and Scattering Media Using the Discrete Transfer Method", In W. A. Fiveland et al., editor, Fundamentals of Radiation Heat Transfer, volume 160, pages 17-26. ASME HTD, 1991.
▪ Modello di radiazione superficie a superficie (S2S)
Riferimenti: R. Siegel and J. R. Howell, "Thermal Radiation Heat Transfer", Hemisphere Publishing Corporation, Washington DC, 1992.
▪ Modello di radiazione delle ordinate discrete (DO)
Riferimenti: G. D. Raithby and E. H. Chui, A Finite-Volume "Method for Predicting a Radiant Heat Transfer in Enclosures with Participating Media", J. Heat Transfer, 112:415-423, 1990.
Riferimenti: E. H. Chui and G. D. Raithby, "Computation of Radiant Heat Transfer on a Non-Orthogonal Mesh Using the Finite-Volume Method", Numerical Heat Transfer, Part B, 23:269-288, 1993.
Ogni modello presenta vantaggi e limitazioni in termini di precisione e di costo. Ad esempio, sebbene il modello di Rosseland non risolva un'equazione di trasferimento per la radiazione incidente, rappresenta il modello di radiazione più veloce e richiede la minor quantità di memoria aggiuntiva. Il modello di Rosseland può essere utilizzato solo per mezzi otticamente spessi (lo spessore ottico è il logaritmo naturale del rapporto tra potenza radiante incidente e trasmessa in un mezzo) a causa della sua eccessiva semplificazione dell'equazione del trasferimento radiativo.
Il modello radiativo delle ordinate discrete (DO) trasforma l'equazione 2.287 in un'equazione di trasferimento per l'intensità della radiazione nelle coordinate spaziali 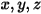 e la risolve su un numero finito di angoli solidi distinti associati alla direzione del vettore
e la risolve su un numero finito di angoli solidi distinti associati alla direzione del vettore 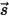 . Il numero degli angoli solidi selezionati determina direttamente la precisione e il costo del calcolo. L'approccio della modellazione basata sulle DO è inoltre identico all'approccio utilizzato per le equazioni del flusso di un fluido e dell'energia. Attualmente è il modello di radiazione più generico che si estende sull'intera gamma di spessori ottici e che può essere applicato a problemi che variano dalla radiazione superficie a superficie alla radiazione partecipante, ad esempio in un sistema di combustione. Il costo del calcolo del modello DO è tuttavia elevato per le radiazioni di corpi non grigi.
. Il numero degli angoli solidi selezionati determina direttamente la precisione e il costo del calcolo. L'approccio della modellazione basata sulle DO è inoltre identico all'approccio utilizzato per le equazioni del flusso di un fluido e dell'energia. Attualmente è il modello di radiazione più generico che si estende sull'intera gamma di spessori ottici e che può essere applicato a problemi che variano dalla radiazione superficie a superficie alla radiazione partecipante, ad esempio in un sistema di combustione. Il costo del calcolo del modello DO è tuttavia elevato per le radiazioni di corpi non grigi.
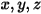 e la risolve su un numero finito di angoli solidi distinti associati alla direzione del vettore
e la risolve su un numero finito di angoli solidi distinti associati alla direzione del vettore 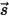 . Il numero degli angoli solidi selezionati determina direttamente la precisione e il costo del calcolo. L'approccio della modellazione basata sulle DO è inoltre identico all'approccio utilizzato per le equazioni del flusso di un fluido e dell'energia. Attualmente è il modello di radiazione più generico che si estende sull'intera gamma di spessori ottici e che può essere applicato a problemi che variano dalla radiazione superficie a superficie alla radiazione partecipante, ad esempio in un sistema di combustione. Il costo del calcolo del modello DO è tuttavia elevato per le radiazioni di corpi non grigi.
. Il numero degli angoli solidi selezionati determina direttamente la precisione e il costo del calcolo. L'approccio della modellazione basata sulle DO è inoltre identico all'approccio utilizzato per le equazioni del flusso di un fluido e dell'energia. Attualmente è il modello di radiazione più generico che si estende sull'intera gamma di spessori ottici e che può essere applicato a problemi che variano dalla radiazione superficie a superficie alla radiazione partecipante, ad esempio in un sistema di combustione. Il costo del calcolo del modello DO è tuttavia elevato per le radiazioni di corpi non grigi.Tra i modelli di radiazione sopra indicati, quello superficie a superficie (S2S) è particolarmente adatto per la modellazione del trasferimento radiativo su superfici a estensione finita senza la considerazione dei mezzi partecipanti. Esempi tipici sono le stufe radiative e i sistemi di sottocofano e sottoscocca dei veicoli. In queste situazioni, i modelli di radiazione per la radiazione partecipante sono talvolta inefficienti. Rispetto al modello di radiazione DO, il modello S2S ha un tempo per iterazione più veloce, sebbene il calcolo del fattore di vista in sé possa richiedere un utilizzo elevato della CPU. In Creo Flow Analysis, il modello per il trasferimento termico radiativo attualmente utilizzato è il modello di radiazione S2S.
Modello di radiazione superficie a superficie (S2S)
Il modello di radiazione superficie a superficie è alla base dello scambio di radiazioni in un'estensione finita di superfici diffuse grigie senza mezzi partecipanti. Lo scambio di energia radiativa superficie a superficie dipende da due fattori principali: le caratteristiche radiative delle superfici interessate e i parametri geometrici, comprese le aree e le forme delle superfici, e la posizione relativa delle due superfici (distanza di separazione e orientazione). Nel modello di radiazione S2S, il trasferimento termico radiativo della superficie viene considerato dal modello di radiazione diffusa grigia, mentre i parametri geometrici sono tenuti in considerazione da una funzione geometrica denominata fattore di vista.
• Radiazione diffusa di corpo grigio
Il modello di radiazione S2S presuppone che le superfici siano grigie e diffuse (radiazione di corpo grigio). Per una superficie grigia, sia l'emissività 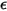 che il coefficiente di assorbimento
che il coefficiente di assorbimento 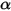 delle superfici sono indipendenti dalla lunghezza d'onda dei raggi entranti e uscenti. Secondo la legge di Kirchhoff sulla radiazione termica nell'equazione 2.274, l'emissività è uguale al coefficiente di assorbimento:
delle superfici sono indipendenti dalla lunghezza d'onda dei raggi entranti e uscenti. Secondo la legge di Kirchhoff sulla radiazione termica nell'equazione 2.274, l'emissività è uguale al coefficiente di assorbimento:
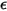 che il coefficiente di assorbimento
che il coefficiente di assorbimento 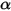 delle superfici sono indipendenti dalla lunghezza d'onda dei raggi entranti e uscenti. Secondo la legge di Kirchhoff sulla radiazione termica nell'equazione 2.274, l'emissività è uguale al coefficiente di assorbimento:
delle superfici sono indipendenti dalla lunghezza d'onda dei raggi entranti e uscenti. Secondo la legge di Kirchhoff sulla radiazione termica nell'equazione 2.274, l'emissività è uguale al coefficiente di assorbimento: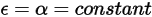
Equazione 2.291
Inoltre, nell'ipotesi di una superficie diffusa, non avviene alcuna riflessione speculare sulla superficie e la riflettività (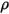 ) di radiazione incidente sulla superficie è isotropa rispetto all'angolo solido. In base all'equazione 2.290, la riflettività della superficie viene determinata come segue:
) di radiazione incidente sulla superficie è isotropa rispetto all'angolo solido. In base all'equazione 2.290, la riflettività della superficie viene determinata come segue:
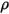 ) di radiazione incidente sulla superficie è isotropa rispetto all'angolo solido. In base all'equazione 2.290, la riflettività della superficie viene determinata come segue:
) di radiazione incidente sulla superficie è isotropa rispetto all'angolo solido. In base all'equazione 2.290, la riflettività della superficie viene determinata come segue: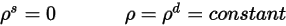
Equazione 2.292
dove
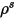 | superficie speculare |
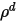 | riflettività diffusa |
Per una superficie non opaca o semi-trasparente, anche la trasmissività 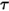 è indipendente dalle lunghezze d'onda:
è indipendente dalle lunghezze d'onda:
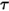 è indipendente dalle lunghezze d'onda:
è indipendente dalle lunghezze d'onda: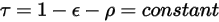
Equazione 2.293
Il modello superficie a superficie diffuso di corpo grigio presuppone che lo scambio di energia radiativa tra le superfici non sia in alcun modo influenzato dal mezzo che le separa. Pertanto, se una determinata quantità di energia radiante 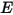 è incidente su una superficie per unità di area (irraggiamento), le porzioni dell'energia radiativa riflesse, assorbite e trasmesse sono rispettivamente
è incidente su una superficie per unità di area (irraggiamento), le porzioni dell'energia radiativa riflesse, assorbite e trasmesse sono rispettivamente 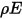 ,
, 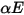 e
e 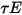 . Poiché per la maggior parte delle applicazioni le superfici sono opache alle radiazioni termiche nello spettro infrarosso, le superfici radiative possono essere ulteriormente considerate opache. La trasmissività, pertanto, può essere trascurata
. Poiché per la maggior parte delle applicazioni le superfici sono opache alle radiazioni termiche nello spettro infrarosso, le superfici radiative possono essere ulteriormente considerate opache. La trasmissività, pertanto, può essere trascurata 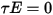 . In base all'equazione 2.273 e all'equazione 2.274, la riflettività della superficie
. In base all'equazione 2.273 e all'equazione 2.274, la riflettività della superficie 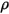 viene espressa nel modo seguente:
viene espressa nel modo seguente:
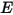 è incidente su una superficie per unità di area (irraggiamento), le porzioni dell'energia radiativa riflesse, assorbite e trasmesse sono rispettivamente
è incidente su una superficie per unità di area (irraggiamento), le porzioni dell'energia radiativa riflesse, assorbite e trasmesse sono rispettivamente 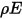 ,
, 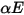 e
e 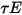 . Poiché per la maggior parte delle applicazioni le superfici sono opache alle radiazioni termiche nello spettro infrarosso, le superfici radiative possono essere ulteriormente considerate opache. La trasmissività, pertanto, può essere trascurata
. Poiché per la maggior parte delle applicazioni le superfici sono opache alle radiazioni termiche nello spettro infrarosso, le superfici radiative possono essere ulteriormente considerate opache. La trasmissività, pertanto, può essere trascurata 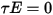 . In base all'equazione 2.273 e all'equazione 2.274, la riflettività della superficie
. In base all'equazione 2.273 e all'equazione 2.274, la riflettività della superficie 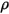 viene espressa nel modo seguente:
viene espressa nel modo seguente: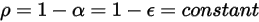
Equazione 2.294
nell'ipotesi della radiazione diffusa di corpo grigio della superficie, l'equazione di modellazione S2S viene costruita in base alla conservazione di energia su ogni superficie.
• Equazione di modellazione S2S
Il presupposto principale del modello S2S è che in un sistema chiuso, il trasferimento termico radiativo si verifica solo tra superfici diffuse di corpi grigi (radiazione su un corpo grigio). È possibile ignorare l'assorbimento, l'emissione o la dispersione delle radiazioni nel mezzo che separa le superfici. Si può pertanto considerare solo la radiazione superficie a superficie per l'analisi numerica.
Il flusso di energia radiativa che lascia una determinata superficie è costituito da energia emessa e riflessa direttamente. Il flusso di energia riflesso dipende dal flusso di energia incidente proveniente dall'ambiente circostante, che può quindi essere espresso in termini di flusso di energia che lascia tutte le altre superfici. Per calcolare il flusso di energia radiativo netto in una superficie, è opportuno definire la radiosità 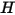 , che è la somma della potenza emissiva per unità di area (emittenza)
, che è la somma della potenza emissiva per unità di area (emittenza) 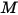 e la parte riflessa della potenza di radiazione ricevuta dalla superficie per unità di area (irradiamento)
e la parte riflessa della potenza di radiazione ricevuta dalla superficie per unità di area (irradiamento) 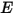 :
:
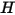 , che è la somma della potenza emissiva per unità di area (emittenza)
, che è la somma della potenza emissiva per unità di area (emittenza) 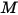 e la parte riflessa della potenza di radiazione ricevuta dalla superficie per unità di area (irradiamento)
e la parte riflessa della potenza di radiazione ricevuta dalla superficie per unità di area (irradiamento) 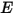 :
: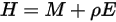
Equazione 2.295
Per una superficie opaca, 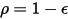 , si ha la radiosità:
, si ha la radiosità:
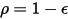 , si ha la radiosità:
, si ha la radiosità: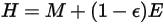
equazione 2.296
nell'ipotesi del modello S2S, pertanto, è possibile formulare il sistema di equazioni lineari riportato di seguito per calcolare la radiosità su ciascuna superficie in un sistema chiuso. Supponendo che 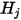 rappresenti la radiosità su una superficie arbitraria
rappresenti la radiosità su una superficie arbitraria 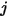 ,
, 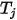 sia la temperatura della superficie e
sia la temperatura della superficie e 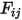 sia il fattore di vista tra la superficie
sia il fattore di vista tra la superficie 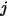 e
e  , si ottiene la radiosità nella superficie
, si ottiene la radiosità nella superficie  :
:
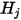 rappresenti la radiosità su una superficie arbitraria
rappresenti la radiosità su una superficie arbitraria 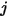 ,
, 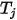 sia la temperatura della superficie e
sia la temperatura della superficie e 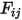 sia il fattore di vista tra la superficie
sia il fattore di vista tra la superficie 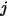 e
e  , si ottiene la radiosità nella superficie
, si ottiene la radiosità nella superficie  :
: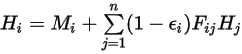
equazione 2.297
dove 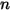 è il numero delle superfici interessate dal trasferimento termico radiativo. Introducendo il simbolo di Kronecker
è il numero delle superfici interessate dal trasferimento termico radiativo. Introducendo il simbolo di Kronecker 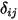 e applicando la legge di Stefan-Boltzmann sulla radiazione di un corpo grigio, equazione 2.278, è possibile modificare l'equazione 2.297 e derivare l'equazione di modellazione S2S:
e applicando la legge di Stefan-Boltzmann sulla radiazione di un corpo grigio, equazione 2.278, è possibile modificare l'equazione 2.297 e derivare l'equazione di modellazione S2S:
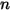 è il numero delle superfici interessate dal trasferimento termico radiativo. Introducendo il simbolo di Kronecker
è il numero delle superfici interessate dal trasferimento termico radiativo. Introducendo il simbolo di Kronecker 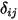 e applicando la legge di Stefan-Boltzmann sulla radiazione di un corpo grigio, equazione 2.278, è possibile modificare l'equazione 2.297 e derivare l'equazione di modellazione S2S:
e applicando la legge di Stefan-Boltzmann sulla radiazione di un corpo grigio, equazione 2.278, è possibile modificare l'equazione 2.297 e derivare l'equazione di modellazione S2S: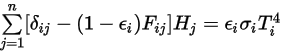
equazione 2.298
Con il fattore di vista precalcolato 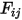 , il sistema di equazione 2.298 lineare viene risolto per ottenere
, il sistema di equazione 2.298 lineare viene risolto per ottenere 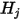 per le superfici partecipanti. La potenza termica radiativa netta su ciascuna superficie viene quindi calcolata facilmente. Per la superficie
per le superfici partecipanti. La potenza termica radiativa netta su ciascuna superficie viene quindi calcolata facilmente. Per la superficie  , la potenza termica radiativa netta
, la potenza termica radiativa netta 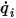 è la differenza tra la radiazione uscente (
è la differenza tra la radiazione uscente (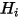 ) e la radiazione entrante (
) e la radiazione entrante (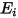 ) per unità di area. In base all'equazione 2.278 e all'equazione 2.296 è possibile derivare la seguente formulazione del flusso:
) per unità di area. In base all'equazione 2.278 e all'equazione 2.296 è possibile derivare la seguente formulazione del flusso:
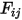 , il sistema di equazione 2.298 lineare viene risolto per ottenere
, il sistema di equazione 2.298 lineare viene risolto per ottenere 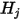 per le superfici partecipanti. La potenza termica radiativa netta su ciascuna superficie viene quindi calcolata facilmente. Per la superficie
per le superfici partecipanti. La potenza termica radiativa netta su ciascuna superficie viene quindi calcolata facilmente. Per la superficie  , la potenza termica radiativa netta
, la potenza termica radiativa netta 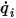 è la differenza tra la radiazione uscente (
è la differenza tra la radiazione uscente (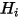 ) e la radiazione entrante (
) e la radiazione entrante (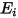 ) per unità di area. In base all'equazione 2.278 e all'equazione 2.296 è possibile derivare la seguente formulazione del flusso:
) per unità di area. In base all'equazione 2.278 e all'equazione 2.296 è possibile derivare la seguente formulazione del flusso: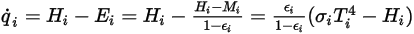
Equazione 2.299
Per una determinata area di superficie 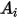 la potenza termica di radiazione netta che lascia la superficie
la potenza termica di radiazione netta che lascia la superficie 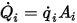 viene calcolata come segue:
viene calcolata come segue:
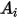 la potenza termica di radiazione netta che lascia la superficie
la potenza termica di radiazione netta che lascia la superficie 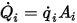 viene calcolata come segue:
viene calcolata come segue: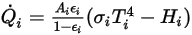
Equazione 2.300
Il modello S2S è composto da un sistema di equazioni lineari sotto forma di equazione 2.298. Il vantaggio offerto dall'applicazione del modello consiste nel fatto che per i fattori di vista e le temperature specificati si calcolano i flussi di calore netti risolvendo un sistema di equazioni lineari, calcolate applicando algoritmi numerici. Tuttavia, la difficoltà principale nell'applicazione del modello superficie a superficie proposto consiste nel calcolo dei fattori di vista 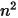 , per un numero n di superfici partecipanti. Questo calcolo può richiedere molto tempo, in particolare in presenza di un numero elevato di superfici.
, per un numero n di superfici partecipanti. Questo calcolo può richiedere molto tempo, in particolare in presenza di un numero elevato di superfici.
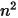 , per un numero n di superfici partecipanti. Questo calcolo può richiedere molto tempo, in particolare in presenza di un numero elevato di superfici.
, per un numero n di superfici partecipanti. Questo calcolo può richiedere molto tempo, in particolare in presenza di un numero elevato di superfici.Calcolo del fattore di vista
Nell'equazione 2.298 della modellazione S2S, il fattore di vista 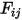 è la proporzione della radiazione che lascia la superficie
è la proporzione della radiazione che lascia la superficie  e raggiunge la superficie
e raggiunge la superficie 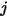 . Come mostrato nella figura 2.37, supponendo che
. Come mostrato nella figura 2.37, supponendo che 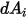 sia l'area differenziale sulla superficie
sia l'area differenziale sulla superficie  e che
e che 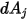 sia l'area differenziale sulla superficie
sia l'area differenziale sulla superficie 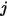 e supponendo che la distanza tra
e supponendo che la distanza tra 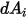 e
e 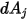 sia
sia 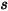 , si esprime il fattore di vista
, si esprime il fattore di vista 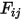 da
da 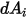 a
a 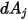 a una distanza
a una distanza 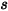 , come segue:
, come segue:
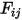 è la proporzione della radiazione che lascia la superficie
è la proporzione della radiazione che lascia la superficie  e raggiunge la superficie
e raggiunge la superficie 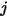 . Come mostrato nella figura 2.37, supponendo che
. Come mostrato nella figura 2.37, supponendo che 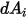 sia l'area differenziale sulla superficie
sia l'area differenziale sulla superficie  e che
e che 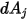 sia l'area differenziale sulla superficie
sia l'area differenziale sulla superficie 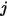 e supponendo che la distanza tra
e supponendo che la distanza tra 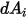 e
e 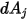 sia
sia 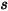 , si esprime il fattore di vista
, si esprime il fattore di vista 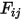 da
da 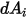 a
a 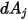 a una distanza
a una distanza 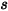 , come segue:
, come segue: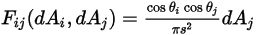
Equazione 2.301
dove 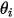 e
e 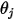 sono l'angolo tra le direzioni normali della superficie e un raggio tra le due aree differenziali.
sono l'angolo tra le direzioni normali della superficie e un raggio tra le due aree differenziali.
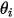 e
e 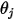 sono l'angolo tra le direzioni normali della superficie e un raggio tra le due aree differenziali.
sono l'angolo tra le direzioni normali della superficie e un raggio tra le due aree differenziali.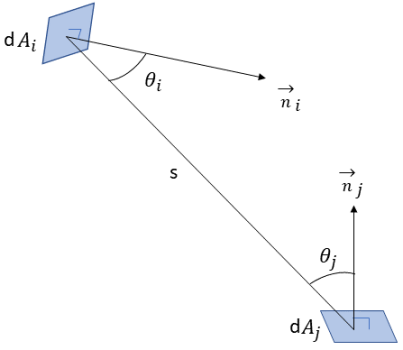
Illustrazione 2.37
Se 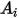 e
e 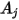 sono rispettivamente le aree di superficie specificate
sono rispettivamente le aree di superficie specificate  e
e 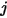 , il fattore di vista da superficie
, il fattore di vista da superficie  a superficie
a superficie 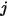 è l'integrale mediato sull'area dell'equazione 2.301 sulle superfici
è l'integrale mediato sull'area dell'equazione 2.301 sulle superfici  e
e 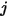 :
:
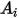 e
e 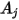 sono rispettivamente le aree di superficie specificate
sono rispettivamente le aree di superficie specificate  e
e 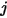 , il fattore di vista da superficie
, il fattore di vista da superficie  a superficie
a superficie 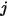 è l'integrale mediato sull'area dell'equazione 2.301 sulle superfici
è l'integrale mediato sull'area dell'equazione 2.301 sulle superfici  e
e 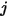 :
: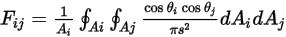
Equazione 2.302
La radiazione superficie a superficie si verifica solo quando le due superfici sono reciprocamente visibili oppure il fattore di vista è diverso da zero. Se si introduce il simbolo di Kronecker 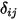 in relazione alla visibilità tra
in relazione alla visibilità tra 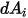 e
e 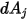 :
:
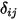 in relazione alla visibilità tra
in relazione alla visibilità tra 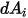 e
e 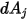 :
: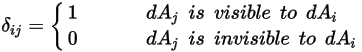
Equazione 2.303
è possibile riscrivere l'equazione 2.302 come segue:
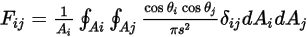
Equazione 2.304
Per due superfici reciprocamente visibili, una determinata superficie  irradia soltanto una frazione dell'energia radiativa uscente alla superficie
irradia soltanto una frazione dell'energia radiativa uscente alla superficie 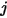 , come mostrato nella figura 2.378. Pertanto, il fattore di vista senza quote
, come mostrato nella figura 2.378. Pertanto, il fattore di vista senza quote 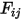 rappresenta la frazione di energia che lascia la superficie
rappresenta la frazione di energia che lascia la superficie  e raggiunge la superficie
e raggiunge la superficie 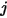 . Le caratteristiche sono indicate nell'elenco riportato di seguito.
. Le caratteristiche sono indicate nell'elenco riportato di seguito.
 irradia soltanto una frazione dell'energia radiativa uscente alla superficie
irradia soltanto una frazione dell'energia radiativa uscente alla superficie 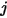 , come mostrato nella figura 2.378. Pertanto, il fattore di vista senza quote
, come mostrato nella figura 2.378. Pertanto, il fattore di vista senza quote 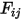 rappresenta la frazione di energia che lascia la superficie
rappresenta la frazione di energia che lascia la superficie  e raggiunge la superficie
e raggiunge la superficie 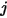 . Le caratteristiche sono indicate nell'elenco riportato di seguito.
. Le caratteristiche sono indicate nell'elenco riportato di seguito.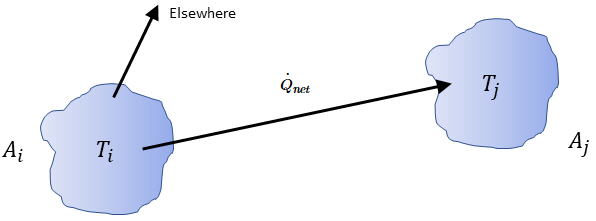
Illustrazione 2.378
• Sommatoria dei fattori di vista - Poiché la radiazione che lascia una superficie viene conservata, la somma di tutti i fattori di vista di una determinata superficie  è l'unità. Per il sistema chiuso di superfici
è l'unità. Per il sistema chiuso di superfici 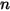 si ha
si ha
 è l'unità. Per il sistema chiuso di superfici
è l'unità. Per il sistema chiuso di superfici 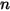 si ha
si ha
Equazione 2.305
• Superfici visibili a se stesse - Poiché la radiazione viaggia in linea retta, nessun raggio di radiazione da una superficie convessa può lasciare la superficie e colpire la stessa superficie in un secondo momento. Di conseguenza, le superfici convesse non sono visibili a se stesse:
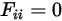
Equazione 2.306
Nelle superfici concave, il raggio uscente da una posizione sulla superficie può colpire la stessa superficie in un secondo momento in una posizione diversa. Ne deriva che la superficie concava può essere visibile a se stessa:
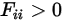
Equazione 2.307
• Sovrapposizione - Per un sistema di 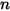 superfici, se una data superficie
superfici, se una data superficie  irradia numero
irradia numero 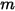 di superfici (
di superfici (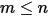 ), il fattore di vista tra la superficie
), il fattore di vista tra la superficie  e il numero
e il numero 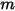 di superfici equivale alla somma dei fattori di vista tra la superficie
di superfici equivale alla somma dei fattori di vista tra la superficie  e ciascuna superficie del numero
e ciascuna superficie del numero 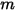 di superfici:
di superfici:
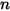 superfici, se una data superficie
superfici, se una data superficie  irradia numero
irradia numero 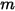 di superfici (
di superfici (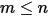 ), il fattore di vista tra la superficie
), il fattore di vista tra la superficie  e il numero
e il numero 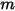 di superfici equivale alla somma dei fattori di vista tra la superficie
di superfici equivale alla somma dei fattori di vista tra la superficie  e ciascuna superficie del numero
e ciascuna superficie del numero 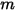 di superfici:
di superfici: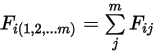
Equazione 2.308
La regola di sovrapposizione o regola di sommatoria è utile quando una geometria non è disponibile con determinati grafici. La regola di sovrapposizione consente di esprimere la geometria ricercata utilizzando la somma o la differenza di geometrie note.
• Reciprocità - L'equazione 2.304 definisce il fattore di vista 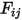 come la frazione dell'energia radiativa che lascia la superficie
come la frazione dell'energia radiativa che lascia la superficie  e raggiunge la superficie
e raggiunge la superficie 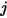 . Analogamente, il fattore di vista
. Analogamente, il fattore di vista 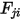 che è la frazione di energia che lascia la superficie
che è la frazione di energia che lascia la superficie 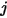 e raggiunge la superficie
e raggiunge la superficie  viene espresso come segue:
viene espresso come segue:
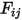 come la frazione dell'energia radiativa che lascia la superficie
come la frazione dell'energia radiativa che lascia la superficie  e raggiunge la superficie
e raggiunge la superficie 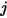 . Analogamente, il fattore di vista
. Analogamente, il fattore di vista 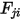 che è la frazione di energia che lascia la superficie
che è la frazione di energia che lascia la superficie 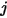 e raggiunge la superficie
e raggiunge la superficie  viene espresso come segue:
viene espresso come segue: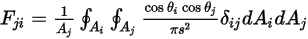
Equazione 2.309
Confrontando l'equazione 2.309 con l'equazione 2.304, si ottiene la seguente relazione:
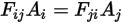
Equazione 2.310
Con l'equazione 2.310 si fa riferimento alla reciprocità dei fattori di vista. Il teorema della reciprocità consente di calcolare direttamente solo una delle coppie di fattori di vista.
Clustering
Il modello di radiazione S2S è dispendioso dal punto di vista del calcolo quando il numero di superfici irradianti è alto. Per contenere il tempo di calcolo e la richiesta di spazio di memorizzazione, è possibile ridurre il numero di superfici irradianti raggruppando un certo numero di facce delle celle limite adiacenti per creare cluster di superfici. La radiosità (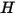 ) viene così calcolata in base ai cluster di superfici. Questi valori vengono quindi distribuiti alle facce delle celle limite all'interno di ciascun cluster per calcolare le temperature della parete. Poiché i termini dell'origine di radiazione sono altamente non lineari (proporzionali alla quarta potenza della temperatura), è necessario assicurarsi di calcolare la temperatura media dei cluster di superfici e distribuire i termini dell'origine e del flusso in modo appropriato tra le facce limite che formano i cluster.
) viene così calcolata in base ai cluster di superfici. Questi valori vengono quindi distribuiti alle facce delle celle limite all'interno di ciascun cluster per calcolare le temperature della parete. Poiché i termini dell'origine di radiazione sono altamente non lineari (proporzionali alla quarta potenza della temperatura), è necessario assicurarsi di calcolare la temperatura media dei cluster di superfici e distribuire i termini dell'origine e del flusso in modo appropriato tra le facce limite che formano i cluster.
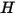 ) viene così calcolata in base ai cluster di superfici. Questi valori vengono quindi distribuiti alle facce delle celle limite all'interno di ciascun cluster per calcolare le temperature della parete. Poiché i termini dell'origine di radiazione sono altamente non lineari (proporzionali alla quarta potenza della temperatura), è necessario assicurarsi di calcolare la temperatura media dei cluster di superfici e distribuire i termini dell'origine e del flusso in modo appropriato tra le facce limite che formano i cluster.
) viene così calcolata in base ai cluster di superfici. Questi valori vengono quindi distribuiti alle facce delle celle limite all'interno di ciascun cluster per calcolare le temperature della parete. Poiché i termini dell'origine di radiazione sono altamente non lineari (proporzionali alla quarta potenza della temperatura), è necessario assicurarsi di calcolare la temperatura media dei cluster di superfici e distribuire i termini dell'origine e del flusso in modo appropriato tra le facce limite che formano i cluster.La temperatura del cluster di superfici è ottenuta dal calcolo della media in base all'area della temperatura della faccia limite come illustrato nell'equazione seguente:
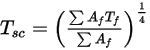
Equazione 2.311
dove 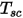 è la temperatura del cluster di superfici, mentre
è la temperatura del cluster di superfici, mentre 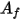 e
e 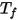 sono l'area e la temperatura della faccia della cella limite nelle simulazioni CFA. La sommatoria viene eseguita su tutte le facce all'interno di un cluster di superfici.
sono l'area e la temperatura della faccia della cella limite nelle simulazioni CFA. La sommatoria viene eseguita su tutte le facce all'interno di un cluster di superfici.
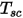 è la temperatura del cluster di superfici, mentre
è la temperatura del cluster di superfici, mentre 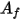 e
e 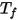 sono l'area e la temperatura della faccia della cella limite nelle simulazioni CFA. La sommatoria viene eseguita su tutte le facce all'interno di un cluster di superfici.
sono l'area e la temperatura della faccia della cella limite nelle simulazioni CFA. La sommatoria viene eseguita su tutte le facce all'interno di un cluster di superfici.