Movimenti di un corpo rigido
Nelle simulazioni, le superfici di un oggetto solido costituiscono in genere limiti di parete in un dominio di flusso. Quando una superficie oppure un oggetto solido è sottoposto a forze dinamiche e meccaniche e all'effetto termico, lo squilibrio delle forze nette può causare il movimento o la deformazione del corpo. Un oggetto solido viene in genere considerato come un corpo rigido nelle simulazioni di flusso. Di conseguenza, per un oggetto solido sottoposto a squilibri di forze viene presupposto che possa spostarsi linearmente (traslazione) e/o angolarmente (rotazione) senza deformazione. Per un dominio computazionale di Creo Flow Analysis, tuttavia, il movimento dei limiti può determinare il cambiamento del dominio e di conseguenza la deformazione della mesh del volume, come descritto per il modulo Flusso (Flow).
Per un corpo rigido, le equazioni che regolano i movimenti sono derivate direttamente dalla conservazione del momento lineare e angolare.
• Momento lineare (traslazione)
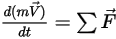
Equazione 2.426
• Momento angolare (rotazione)
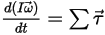
Equazione 2.427
Nell'equazione 2.426, 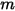 è la massa dell'oggetto mobile,
è la massa dell'oggetto mobile, 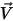 ⃗ è la velocità lineare/transizionale e
⃗ è la velocità lineare/transizionale e 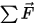 ⃗ rappresenta le forze totali/nette esercitate sul corpo in traslazione. Nell'equazione 2.427,
⃗ rappresenta le forze totali/nette esercitate sul corpo in traslazione. Nell'equazione 2.427, 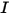 è il momento di inerzia,
è il momento di inerzia, 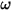 ⃗ è la velocità angolare e
⃗ è la velocità angolare e 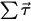 ⃗ è la coppia totale/netta esercitata sul corpo in rotazione.
⃗ è la coppia totale/netta esercitata sul corpo in rotazione.
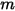 è la massa dell'oggetto mobile,
è la massa dell'oggetto mobile, 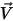 ⃗ è la velocità lineare/transizionale e
⃗ è la velocità lineare/transizionale e 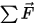 ⃗ rappresenta le forze totali/nette esercitate sul corpo in traslazione. Nell'equazione 2.427,
⃗ rappresenta le forze totali/nette esercitate sul corpo in traslazione. Nell'equazione 2.427, 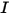 è il momento di inerzia,
è il momento di inerzia, 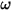 ⃗ è la velocità angolare e
⃗ è la velocità angolare e 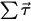 ⃗ è la coppia totale/netta esercitata sul corpo in rotazione.
⃗ è la coppia totale/netta esercitata sul corpo in rotazione.L'equazione 2.426 e l'equazione 2.427 regolano i movimenti generali di un corpo solido, che dispongono di 6 gradi di libertà, 3 per la traslazione e 3 per la rotazione. Creo Flow Analysis considera solo la traslazione e la rotazione a 1 grado di libertà, illustrate in questa sezione.
Traslazione a un grado di libertà
Supponendo che un corpo solido si muova linearmente in una direzione arbitrariamente specificata che rimane invariata ed è definita da un vettore di unità 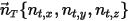 , il movimento traslazionale del corpo viene ridotto a 1 grado di libertà. Di conseguenza, per la conservazione del momento lineare, l'equazione 2.426 diventa un'equazione scalare lungo la direzione di movimento poiché la forza e la velocità di movimento sono espresse in termini di
, il movimento traslazionale del corpo viene ridotto a 1 grado di libertà. Di conseguenza, per la conservazione del momento lineare, l'equazione 2.426 diventa un'equazione scalare lungo la direzione di movimento poiché la forza e la velocità di movimento sono espresse in termini di 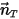 :
:
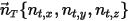 , il movimento traslazionale del corpo viene ridotto a 1 grado di libertà. Di conseguenza, per la conservazione del momento lineare, l'equazione 2.426 diventa un'equazione scalare lungo la direzione di movimento poiché la forza e la velocità di movimento sono espresse in termini di
, il movimento traslazionale del corpo viene ridotto a 1 grado di libertà. Di conseguenza, per la conservazione del momento lineare, l'equazione 2.426 diventa un'equazione scalare lungo la direzione di movimento poiché la forza e la velocità di movimento sono espresse in termini di 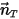 :
: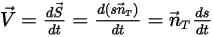
Equazione 2.428
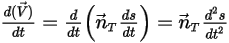
Equazione 2.429
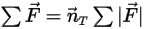
Equazione 2.430
dove 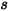 è l'ampiezza del vettore di posizione
è l'ampiezza del vettore di posizione 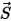 in un punto di interesse sul corpo solido lungo la direzione di movimento
in un punto di interesse sul corpo solido lungo la direzione di movimento 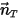 . In un sistema di coordinate cartesiano:
. In un sistema di coordinate cartesiano:
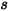 è l'ampiezza del vettore di posizione
è l'ampiezza del vettore di posizione 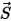 in un punto di interesse sul corpo solido lungo la direzione di movimento
in un punto di interesse sul corpo solido lungo la direzione di movimento 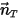 . In un sistema di coordinate cartesiano:
. In un sistema di coordinate cartesiano: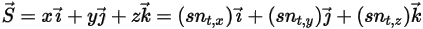
Equazione 2.431
Se la massa del corpo solido rimane una costante ed espandete il termine della forza in modo da includere esplicitamente tutte le forze applicate sul corpo, l'equazione scalare del momento lineare è la seguente:
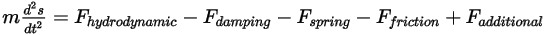
Equazione 2.432
Le forze sul lato destro indicano quanto descritto di seguito.
• Forza idrodinamica  - È costituita da forze di pressione e di taglio, causate dal movimento relativo tra il flusso del fluido e le superfici del corpo solido in contatto con il flusso. Le forze di pressione e di taglio vengono ottenute dalle soluzioni del flusso (quantità di output):
- È costituita da forze di pressione e di taglio, causate dal movimento relativo tra il flusso del fluido e le superfici del corpo solido in contatto con il flusso. Le forze di pressione e di taglio vengono ottenute dalle soluzioni del flusso (quantità di output):
 - È costituita da forze di pressione e di taglio, causate dal movimento relativo tra il flusso del fluido e le superfici del corpo solido in contatto con il flusso. Le forze di pressione e di taglio vengono ottenute dalle soluzioni del flusso (quantità di output):
- È costituita da forze di pressione e di taglio, causate dal movimento relativo tra il flusso del fluido e le superfici del corpo solido in contatto con il flusso. Le forze di pressione e di taglio vengono ottenute dalle soluzioni del flusso (quantità di output):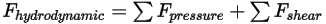
Equazione 2.433
• Forza di smorzamento 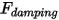 - Forza ritardante causata dall'effetto di smorzamento dell'attrito. È determinata dal movimento dell'oggetto solido e dal coefficiente di smorzamento definito dall'utente
- Forza ritardante causata dall'effetto di smorzamento dell'attrito. È determinata dal movimento dell'oggetto solido e dal coefficiente di smorzamento definito dall'utente 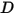 .
.
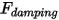 - Forza ritardante causata dall'effetto di smorzamento dell'attrito. È determinata dal movimento dell'oggetto solido e dal coefficiente di smorzamento definito dall'utente
- Forza ritardante causata dall'effetto di smorzamento dell'attrito. È determinata dal movimento dell'oggetto solido e dal coefficiente di smorzamento definito dall'utente 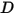 .
.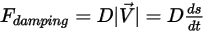
Equazione 2.434
• Forza della molla 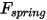 - Dipende dallo spostamento della molla
- Dipende dallo spostamento della molla 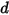 , dalla costante di molla
, dalla costante di molla 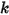 e dalla forza di precarico della molla
e dalla forza di precarico della molla 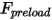 .
.
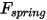 - Dipende dallo spostamento della molla
- Dipende dallo spostamento della molla 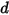 , dalla costante di molla
, dalla costante di molla 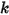 e dalla forza di precarico della molla
e dalla forza di precarico della molla 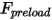 .
.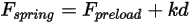
Equazione 2.435
dove lo spostamento della molla 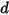 è definito come segue:
è definito come segue:
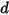 è definito come segue:
è definito come segue: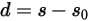
Equazione 2.436
dove 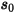 è l'ampiezza del vettore di posizione
è l'ampiezza del vettore di posizione 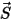 nella posizione precedente
nella posizione precedente 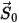 .
.
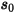 è l'ampiezza del vettore di posizione
è l'ampiezza del vettore di posizione 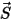 nella posizione precedente
nella posizione precedente 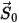 .
.• Forza di attrito - Per tenere conto dell'effetto dell'attrito in un sistema dinamico viene adottato il modello dell'attrito di contatto. La forza di attrito 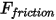 viene modellata come segue:
viene modellata come segue:
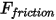 viene modellata come segue:
viene modellata come segue: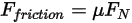
Equazione 2.437
dove 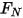 è il componente normale della forza di contatto esercitata sulla superficie solida di interesse. Per il coefficiente di attrito
è il componente normale della forza di contatto esercitata sulla superficie solida di interesse. Per il coefficiente di attrito 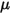 , vengono inoltre introdotti il coefficiente di attrito statico
, vengono inoltre introdotti il coefficiente di attrito statico 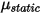 e il coefficiente di attrito radente
e il coefficiente di attrito radente 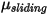 , rispettivamente per i corpi stazionari e mobili:
, rispettivamente per i corpi stazionari e mobili:
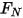 è il componente normale della forza di contatto esercitata sulla superficie solida di interesse. Per il coefficiente di attrito
è il componente normale della forza di contatto esercitata sulla superficie solida di interesse. Per il coefficiente di attrito 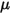 , vengono inoltre introdotti il coefficiente di attrito statico
, vengono inoltre introdotti il coefficiente di attrito statico 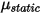 e il coefficiente di attrito radente
e il coefficiente di attrito radente 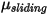 , rispettivamente per i corpi stazionari e mobili:
, rispettivamente per i corpi stazionari e mobili: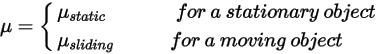
Equazione 2.438
• Forza aggiuntiva 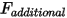 - Viene aggiunta per le ulteriori forze specificate dall'utente.
- Viene aggiunta per le ulteriori forze specificate dall'utente.
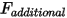 - Viene aggiunta per le ulteriori forze specificate dall'utente.
- Viene aggiunta per le ulteriori forze specificate dall'utente.Rotazione a un grado di libertà
Quando un asse di rotazione arbitrario è definito da un punto (centro dell'asse) 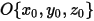 e dal vettore di unità direzionale
e dal vettore di unità direzionale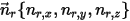 , la rotazione del corpo solido intorno all'asse
, la rotazione del corpo solido intorno all'asse 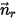 viene ugualmente ridotta a rotazione a 1 grado di libertà. Analogamente, per la conservazione del momento angolare, anche l'equazione 2.427 diventa un'equazione scalare lungo la direzione tangenziale
viene ugualmente ridotta a rotazione a 1 grado di libertà. Analogamente, per la conservazione del momento angolare, anche l'equazione 2.427 diventa un'equazione scalare lungo la direzione tangenziale 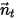 , definita come segue:
, definita come segue:
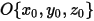 e dal vettore di unità direzionale
e dal vettore di unità direzionale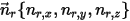 , la rotazione del corpo solido intorno all'asse
, la rotazione del corpo solido intorno all'asse 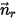 viene ugualmente ridotta a rotazione a 1 grado di libertà. Analogamente, per la conservazione del momento angolare, anche l'equazione 2.427 diventa un'equazione scalare lungo la direzione tangenziale
viene ugualmente ridotta a rotazione a 1 grado di libertà. Analogamente, per la conservazione del momento angolare, anche l'equazione 2.427 diventa un'equazione scalare lungo la direzione tangenziale 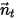 , definita come segue:
, definita come segue: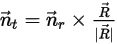
Equazione 2.439
dove 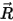 è il vettore che punta dal centro dell'asse a un punto arbitrario
è il vettore che punta dal centro dell'asse a un punto arbitrario 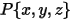 sul corpo solido:
sul corpo solido:
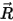 è il vettore che punta dal centro dell'asse a un punto arbitrario
è il vettore che punta dal centro dell'asse a un punto arbitrario 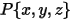 sul corpo solido:
sul corpo solido: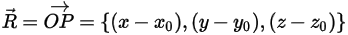
Equazione 2.440
La velocità angolare e la coppia nel punto 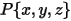 vengono riformulate come segue:
vengono riformulate come segue:
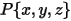 vengono riformulate come segue:
vengono riformulate come segue: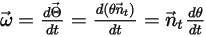
Equazione 2.441
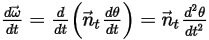
Equazione 2.442
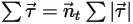
Equazione 2.443
dove 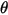 è l'angolo di rotazione del punto
è l'angolo di rotazione del punto 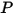 rispetto alla posizione iniziale o di riferimento.
rispetto alla posizione iniziale o di riferimento.
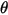 è l'angolo di rotazione del punto
è l'angolo di rotazione del punto 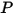 rispetto alla posizione iniziale o di riferimento.
rispetto alla posizione iniziale o di riferimento.Se il momento di inerzia rimane una costante e il termine della coppia viene espanso in modo da includere esplicitamente tutte le coppie applicate sul corpo in rotazione, l'equazione scalare del momento angolare è la seguente:
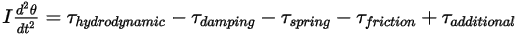
Equazione 2.444
I termini della coppia sul lato destro sono definiti come descritto di seguito.
• Coppia idrodinamica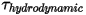 - Combinazione della coppia causata dalle forze di pressione e di taglio:
- Combinazione della coppia causata dalle forze di pressione e di taglio:
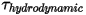 - Combinazione della coppia causata dalle forze di pressione e di taglio:
- Combinazione della coppia causata dalle forze di pressione e di taglio: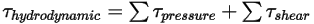
Equazione 2.445
• Coppia smorzamento 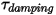 - Dipende dalla velocità di rotazione
- Dipende dalla velocità di rotazione 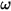 e dal coefficiente di smorzamento definito dall'utente
e dal coefficiente di smorzamento definito dall'utente 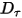 :
:
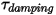 - Dipende dalla velocità di rotazione
- Dipende dalla velocità di rotazione 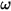 e dal coefficiente di smorzamento definito dall'utente
e dal coefficiente di smorzamento definito dall'utente 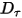 :
: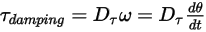
Equazione 2.446
• Coppia elastica 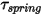 - È indotta dalla torsione che dipende dall'angolo di spostamento
- È indotta dalla torsione che dipende dall'angolo di spostamento 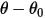 , dalla coppia di precarico definita dall'utente
, dalla coppia di precarico definita dall'utente 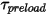 e dalla costante di torsione
e dalla costante di torsione 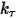 .
.
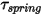 - È indotta dalla torsione che dipende dall'angolo di spostamento
- È indotta dalla torsione che dipende dall'angolo di spostamento 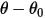 , dalla coppia di precarico definita dall'utente
, dalla coppia di precarico definita dall'utente 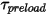 e dalla costante di torsione
e dalla costante di torsione 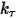 .
.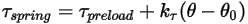
Equazione 2.447
dove 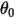 è l'angolo di riferimento. Si tratta in genere della posizione del limite o del volume durante l'impostazione del modello, ma può corrispondere a una posizione diversa. Con spostamento angolare zero, ad esempio, l'angolo di riferimento
è l'angolo di riferimento. Si tratta in genere della posizione del limite o del volume durante l'impostazione del modello, ma può corrispondere a una posizione diversa. Con spostamento angolare zero, ad esempio, l'angolo di riferimento 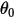 non coincide con la posizione angolare iniziale.
non coincide con la posizione angolare iniziale.
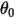 è l'angolo di riferimento. Si tratta in genere della posizione del limite o del volume durante l'impostazione del modello, ma può corrispondere a una posizione diversa. Con spostamento angolare zero, ad esempio, l'angolo di riferimento
è l'angolo di riferimento. Si tratta in genere della posizione del limite o del volume durante l'impostazione del modello, ma può corrispondere a una posizione diversa. Con spostamento angolare zero, ad esempio, l'angolo di riferimento 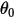 non coincide con la posizione angolare iniziale.
non coincide con la posizione angolare iniziale.• Coppia di attrito - Coppia causata dalla forza di attrito che viene generata quando due oggetti a contatto si muovono. Negli esperimenti, è determinata dalla differenza tra la coppia applicata e la coppia osservata o netta. Dipende dal coefficiente di attrito 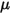 e dalla coppia di contatto causata dalla forza normale
e dalla coppia di contatto causata dalla forza normale 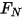 applicata sulla superficie di contatto:
applicata sulla superficie di contatto:
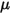 e dalla coppia di contatto causata dalla forza normale
e dalla coppia di contatto causata dalla forza normale 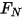 applicata sulla superficie di contatto:
applicata sulla superficie di contatto: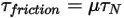
Equazione 2.448
dove 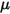 è un parametro definito dall'utente nell'equazione 2.438.
è un parametro definito dall'utente nell'equazione 2.438.
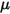 è un parametro definito dall'utente nell'equazione 2.438.
è un parametro definito dall'utente nell'equazione 2.438.• Coppie aggiuntive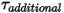 - Vengono aggiunte per le ulteriori coppie specificate dall'utente.
- Vengono aggiunte per le ulteriori coppie specificate dall'utente.
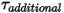 - Vengono aggiunte per le ulteriori coppie specificate dall'utente.
- Vengono aggiunte per le ulteriori coppie specificate dall'utente.Modello di rimbalzo
In molte situazioni, un corpo solido trasla, ruota o effettua entrambe le azioni solo in uno spazio limitato (distanza o angolo limitato), ovvero dispone di una posizione massima, minima o entrambe le posizioni. Ad esempio, come mostrato nell'illustrazione riportata di seguito, quando un pendolo semplice viene rilasciato dalla posizione originale con l'angolo 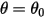 , la forza di richiamo che agisce sulla massa ne provoca l'oscillazione sulla posizione di equilibrio. L'angolo massimo su entrambi i lati della posizione di equilibrio
, la forza di richiamo che agisce sulla massa ne provoca l'oscillazione sulla posizione di equilibrio. L'angolo massimo su entrambi i lati della posizione di equilibrio 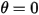 dipende dalla posizione di rilascio
dipende dalla posizione di rilascio 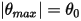 . In assenza di attrito (rotazione senza attrito e nel vuoto), l'angolo massimo rimane invariato e il pendolo oscilla avanti e indietro in modo permanente con le stesse posizioni estreme. Quando però un pendolo si trova nell'atmosfera, ad esempio, la resistenza dell'aria (smorzamento) causa una riduzione dell'angolo di oscillazione massimo nel tempo e infine l'arresto nella posizione di equilibrio.
. In assenza di attrito (rotazione senza attrito e nel vuoto), l'angolo massimo rimane invariato e il pendolo oscilla avanti e indietro in modo permanente con le stesse posizioni estreme. Quando però un pendolo si trova nell'atmosfera, ad esempio, la resistenza dell'aria (smorzamento) causa una riduzione dell'angolo di oscillazione massimo nel tempo e infine l'arresto nella posizione di equilibrio.
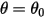 , la forza di richiamo che agisce sulla massa ne provoca l'oscillazione sulla posizione di equilibrio. L'angolo massimo su entrambi i lati della posizione di equilibrio
, la forza di richiamo che agisce sulla massa ne provoca l'oscillazione sulla posizione di equilibrio. L'angolo massimo su entrambi i lati della posizione di equilibrio 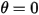 dipende dalla posizione di rilascio
dipende dalla posizione di rilascio 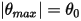 . In assenza di attrito (rotazione senza attrito e nel vuoto), l'angolo massimo rimane invariato e il pendolo oscilla avanti e indietro in modo permanente con le stesse posizioni estreme. Quando però un pendolo si trova nell'atmosfera, ad esempio, la resistenza dell'aria (smorzamento) causa una riduzione dell'angolo di oscillazione massimo nel tempo e infine l'arresto nella posizione di equilibrio.
. In assenza di attrito (rotazione senza attrito e nel vuoto), l'angolo massimo rimane invariato e il pendolo oscilla avanti e indietro in modo permanente con le stesse posizioni estreme. Quando però un pendolo si trova nell'atmosfera, ad esempio, la resistenza dell'aria (smorzamento) causa una riduzione dell'angolo di oscillazione massimo nel tempo e infine l'arresto nella posizione di equilibrio.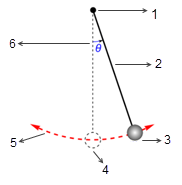
illustrazione
1. Punto di rotazione senza attrito
2. Bacchetta senza massa
3. Peso
4. Posizione di equilibrio
5. Traiettoria del peso
6. Ampiezza
In un ciclo di oscillazione (periodo), inoltre, quando il pendolo raggiunge la posizione più elevata 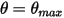 , cambia direzione con perdita totale dell'energia cinetica. Nel pendolo semplice, l'energia cinetica viene completamente trasferita in energia potenziale. Considerando però la resistenza del mezzo, una parte dell'energia cinetica viene persa per superare lo smorzamento viscoso. La forza netta o l'energia potenziale, tuttavia, induce il pendolo a iniziare a muoversi nella direzione opposta verso la posizione di equilibrio, in cui l'energia cinetica (velocità) è massima mentre quella potenziale è minima. In questo caso,
, cambia direzione con perdita totale dell'energia cinetica. Nel pendolo semplice, l'energia cinetica viene completamente trasferita in energia potenziale. Considerando però la resistenza del mezzo, una parte dell'energia cinetica viene persa per superare lo smorzamento viscoso. La forza netta o l'energia potenziale, tuttavia, induce il pendolo a iniziare a muoversi nella direzione opposta verso la posizione di equilibrio, in cui l'energia cinetica (velocità) è massima mentre quella potenziale è minima. In questo caso, 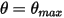 indica una condizione di non rimbalzo per l'equazione del momento angolare a 1 grado di libertà (equazione 2.444).
indica una condizione di non rimbalzo per l'equazione del momento angolare a 1 grado di libertà (equazione 2.444).
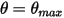 , cambia direzione con perdita totale dell'energia cinetica. Nel pendolo semplice, l'energia cinetica viene completamente trasferita in energia potenziale. Considerando però la resistenza del mezzo, una parte dell'energia cinetica viene persa per superare lo smorzamento viscoso. La forza netta o l'energia potenziale, tuttavia, induce il pendolo a iniziare a muoversi nella direzione opposta verso la posizione di equilibrio, in cui l'energia cinetica (velocità) è massima mentre quella potenziale è minima. In questo caso,
, cambia direzione con perdita totale dell'energia cinetica. Nel pendolo semplice, l'energia cinetica viene completamente trasferita in energia potenziale. Considerando però la resistenza del mezzo, una parte dell'energia cinetica viene persa per superare lo smorzamento viscoso. La forza netta o l'energia potenziale, tuttavia, induce il pendolo a iniziare a muoversi nella direzione opposta verso la posizione di equilibrio, in cui l'energia cinetica (velocità) è massima mentre quella potenziale è minima. In questo caso, 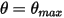 indica una condizione di non rimbalzo per l'equazione del momento angolare a 1 grado di libertà (equazione 2.444).
indica una condizione di non rimbalzo per l'equazione del momento angolare a 1 grado di libertà (equazione 2.444).Oltre alla condizione di non rimbalzo, un corpo mobile nella posizione limite potrebbe non perdere alcuna energia cinetica e rimbalzare (rimbalzo perfetto) oppure perdere solo una parte dell'energia cinetica (rimbalzo parziale). Di conseguenza, quando vengono risolte le equazioni di dinamica a 1 grado di libertà della traslazione e della rotazione (equazione 2.432 ed equazione 2.444) per determinare i movimenti di un corpo solido o di un limite di parete per il dominio di flusso, vengono applicate le tre condizioni di rimbalzo seguenti:
• No Bounce - Modello di default in Creo Flow Analysis. Con questo modello, un limite o un corpo solido, quando raggiunge il proprio limite di movimento, cambia direzione con perdita totale dell'energia cinetica. Rappresentando il rimbalzo e l'incidenza con 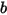 e
e  e la velocità di traslazione e di rotazione (per la sola ampiezza) con
e la velocità di traslazione e di rotazione (per la sola ampiezza) con 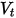 e
e 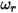 , questo modello di rimbalzo viene espresso come riportato di seguito.
, questo modello di rimbalzo viene espresso come riportato di seguito.
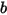 e
e  e la velocità di traslazione e di rotazione (per la sola ampiezza) con
e la velocità di traslazione e di rotazione (per la sola ampiezza) con 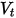 e
e 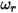 , questo modello di rimbalzo viene espresso come riportato di seguito.
, questo modello di rimbalzo viene espresso come riportato di seguito.◦ Traslazione
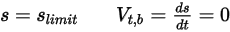
Equazione 2.449
◦ Rotazione
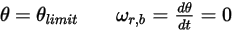
Equazione 2.450
• Rimbalzo parziale - Modello con cui un limite o un corpo solido, quando raggiunge il proprio limite di movimento, cambia direzione con perdita parziale dell'energia cinetica determinata da un fattore specificato dall'utente, 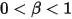 .
.
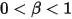 .
.◦ Traslazione
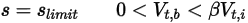
Equazione 2.451
◦ Rotazione
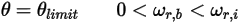
Equazione 2.452
• Rimbalzo perfetto - Modello con cui un limite o un corpo solido, quando raggiunge il proprio limite di movimento, cambia direzione con perdita zero di energia cinetica, 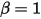 .
.
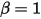 .
.◦ Traslazione

Equazione 2.453
◦ Rotazione

Equazione 2.454