Numerische Überlegungen
In homogenen Mehrphasenmodellen ohne Berücksichtigung von Geschwindigkeitsschlupf ist keine besondere Behandlung erforderlich, um die Mischungsimpulsgleichungen und die Formel für den Flächenvolumenfluss zu lösen. Dies liegt daran, dass es sich dabei um die gleichen Gleichungen wie für Einphasenflüsse mit variabler Dichte handelt. In diesem Thema werden der Aufbau der Druckkorrekturgleichung und die Behandlung der Phasenvolumenanteilsgleichungen behandelt, vor allem Schnittstellenlösungssysteme im VOF-Modell.
Volumenstetigkeitsgleichung
Um die Stetigkeitsrandbedingung einzuhalten und die numerische Stabilität sicherzustellen, baut die Druckkorrekturgleichung auf der Basis der Gesamtvolumenstetigkeit anstatt auf der Massenstetigkeit auf. Wenn Sie die q-te Phasenstetigkeit/Volumenanteil Gleichung 2.57 durch eine Phasenreferenzdichte ρrq teilen und alle Phasen kombinieren, erhalten Sie eine Gesamtvolumenstetigkeitsgleichung, die den Massenerhaltungssatz erfüllt.
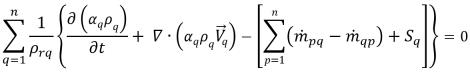
Gleichung 2.135
Hierbei wird die Phasenreferenzdichte normalerweise als Phasendichte ρrq = ρq eingestellt.
Die Einführung von Ω als das Volumen einer Berechnungszelle und das Integrieren von Gleichung 2.135 über das Kontrollvolumen generiert die diskretisierten algebraischen Gleichungen:
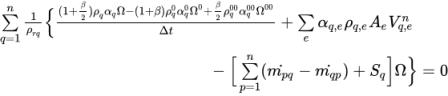
Gleichung 2.136
Wenn Sie denselben Ansatz wie im druckbasierten Einphasen-Gleichungslöser verwenden, der unter Numerik beschrieben wird, und Folgendes annehmen:
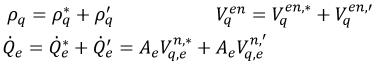
Gleichung 2.137
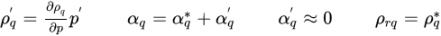
Gleichung 2.138
können Sie die Gleichung 2.136 als folgende Korrekturgleichung neu anordnen:
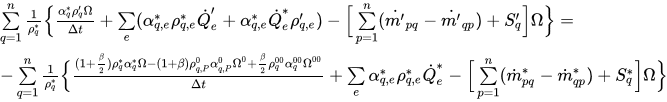
Gleichung 2.139
Hier stellen * und ' alte Werte und Korrekturen dar.
Δt | Zeitschritt |
Ae | Bereich an Fläche e |
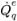 | Volumenfluss |
Gemäß demselben Ansatz wie im druckbasierten Einphasen-Gleichungslöser wenden Sie den SIMPLE-Typ von Algorithmen (Simple, SimpleC und SimpleS) an, um die Geschwindigkeits- und Druckkorrekturen zu verbinden und die Druckkorrekturgleichung für Mehrphasenflüsse zu erhalten:
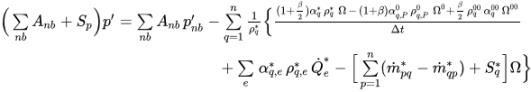
Gleichung 2.140
Dabei gilt:
Anb | Verknüpfungskoeffizient |
Sp | linearisierter Ausdruck |
Phasenvolumenanteilsgleichungen
Für den Transport eines Phasenvolumenanteils gilt die Phasenmassenerhaltung. Da die Gesamtvolumenerhaltung bei der Bildung der Druckkorrekturgleichung angewendet wird, sind die tatsächlichen Gleichungen, die für Phasenvolumenanteile gelöst werden, ebenfalls in der Form der Volumenerhaltung zur numerischen Konsistenz:
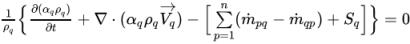
Gleichung 2.141
Normalerweise werden für ein N-Phasensystem nur die Gleichungen (n-1) gelöst, während die n-te Phase aus der physikalischen Randbedingung erlangt wird:
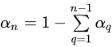
Gleichung 2.142
Nach dem diskretisierenden Ansatz lautet die Integralform der Gleichung 2.141 wie folgt:
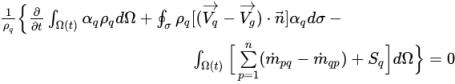
Gleichung 2.143
Wie in den Impuls-, Energie- und Gesamtvolumenerhaltungsgleichungen gegeben sind die räumliche und zeitliche Diskretisierungsmodelle entscheidend für die numerische Genauigkeit. Für die Volumenanteilsgleichungen ist es gängige Praxis, dass zusätzlich zu den standardmäßigen impliziten Zeitschemen der explizite Zeitwert bei hochauflösenden Advektionsschemen verwendet wird, sodass Sie die Schnittstellen in VOF-Modellen genauer erfassen können. Sowohl die impliziten als auch die expliziten VOF-Formeln werden in diesem Abschnitt detailliert beschrieben.
• Implizite VOF-Formel
Bei der impliziten VOF-Formel hat die diskretisierte Phasenvolumenanteilsgleichung den folgenden allgemeinen Ausdruck:
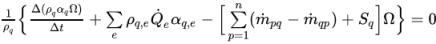
Gleichung 2.144
In dieser Gleichung ist der Phasenvolumenanteil αq im aktuellen Zeitschritt eine Funktion der anderen Größen am aktuellen Zeitschritt. Wie die Impuls-, Energie- und Druckkorrekturgleichungen wird daher die Gleichung 2.144 für den diskretisierten Volumenanteil iterativ in jedem Zeitschritt gelöst. In Creo Flow Analysis ist die implizite Formel wie folgt zusammengefasst:
◦ Advektionsschemen – Der volumetrische Fluss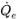 
wird basierend auf dem Flussfeld im aktuellen Zeitschritt berechnet. Der Flächenwert αq,e wird approximiert als Zellenmittenwerte αq,P,αq,E und-gradienten (
,
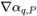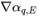) der Nachbarzellen P und E. Wie bei der passiven Skalargleichung haben die Advektionsschemen die allgemeine Form:
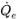wird basierend auf dem Flussfeld im aktuellen Zeitschritt berechnet. Der Flächenwert αq,e wird approximiert als Zellenmittenwerte αq,P,αq,E und-gradienten (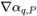,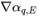) der Nachbarzellen P und E. Wie bei der passiven Skalargleichung haben die Advektionsschemen die allgemeine Form: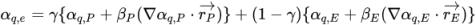
Gleichung 2.145
Unter Verwendung verschiedener Werte für die Parameter γ, βP und βE und der Schemen zur Berechnung der Volumenanteilsgradienten werden vier Advektionsschemen für die Volumenanteilsgleichungen entwickelt: First-Order Upwind, Second-Order Upwind, Center Difference und High Resolution.
◦ Temporale Schemen – Zur Beschreibung des impliziten temporalen Schemas können Sie Gleichung 2.144 im folgenden Ausdruck verallgemeinern:
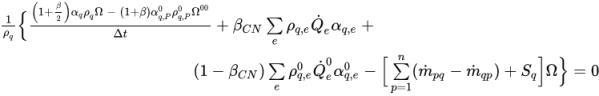
Gleichung 2.146
Die Variablen ohne ein hochgestelltes Zeichen sind die Werte am aktuellen Zeitschritt. Variablen mit dem hochgestellten Zeichen 0 oder 00 geben die Werte an den vorherigen Zeitschritten an.
Die Parameter β und βCN variieren zwischen 0 und 1 und bestimmen die Zeitschemen. Speziell werden drei temporale Schemen für die Diskretisierung der Phasenvolumenanteilsgleichungen angenommen:
▪ Euler First-Order Upwind: β = 0, βCN = 1
▪ Three-Level Second-Order: β = 0, βCN = 1
▪ Crank-Nicolson-Methode: β = 0, βCN = 0.6 (Standardeinstellung)
• Explizite VOF-Formel
Wenn die explizite Formel zum Lösen der VOF-Gleichungen verwendet wird, werden die Phasenvolumenanteile am aktuellen Zeitschritt direkt auf Grundlage bekannter Werte aus dem vorherigen Zeitschritt berechnet. Daher ist für die explizite VOF-Formel keine iterative Lösung für Gleichung 2.144 in jedem Zeitschritt erforderlich. Da jedoch der Rest der Transportgleichungen implizit gelöst wird, ist der für die Volumenanteilsberechnung verwendete Zeitschritt im Allgemeinen kleiner als der für die anderen Transportgleichungen verwendete Zeitschritt. Ein untergeordneter Zeitschritt muss für die explizite VOF-Formel bestimmt werden, der automatisch berechnet wird oder den Sie in Creo Flow Analysis angeben können.
Bei der expliziten Formel wird die diskretisierte Phasenvolumenanteilsgleichung wie folgt formuliert:
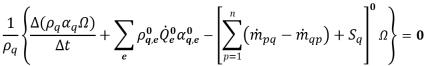
Gleichung 2.147
Hierbei werden sowohl der Advektions- als auch der Quellenausdruck auf der Grundlage der bekannten Werte aus dem vorherigen Zeitschritt berechnet. Der volumetrische Fluss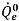 
wird auf dieselbe Weise wie 
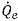in der impliziten Formel berechnet. Der Flächenvolumenanteil 
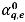kann auch unter Verwendung eines der vier Advektionsschemen geschätzt werden: First-Order Upwind, Second-Order Upwind, Center Difference und High Resolution.
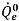wird auf dieselbe Weise wie 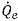in der impliziten Formel berechnet. Der Flächenvolumenanteil 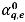kann auch unter Verwendung eines der vier Advektionsschemen geschätzt werden: First-Order Upwind, Second-Order Upwind, Center Difference und High Resolution.Creo Flow Analysis bietet die folgenden drei Algorithmen für die expliziten Zeitverlaufsschemen an:
• Euler First Order Explicit – Die Volumenanteilsgleichung wird wie folgt diskretisiert:
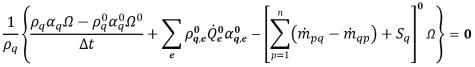
Gleichung 2.148
• Runge-Kutta Second-Order – Die folgende Funktion wird eingeführt:
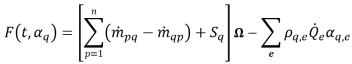
Gleichung 2.149
Die Gleichung 2.147 wird wie folgt umgeschrieben:
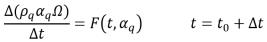
Gleichung 2.150
Anschließend hat das explizite Runge-Kutta-Schema zweiter Ordnung folgende Form:
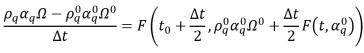
Gleichung 2.151
• Runge-Kutta Fourth-Order – Für die Volumenanteilsgleichung der Phase q hat das explizite Runge-Kutta-Schema vierter Ordnung folgende Form:
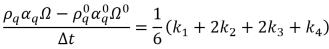
Gleichung 2.152
Dabei gilt:
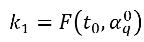
Gleichung 2.153
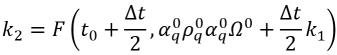
Gleichung 2.154
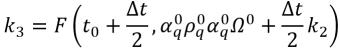
Gleichung 2.155
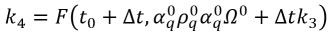
Gleichung 2.156
Beim n-Phasensystem werden in der Regel nur Volumenanteile der Phasen (n-1) gelöst und der restliche Volumenanteil wird aus der physikalischen Randbedingung Gleichung 2.142 entnommen. Sie können jedoch auch alle n Phasenvolumenanteilsgleichungen lösen, und Gleichung 2.142 wird durch Skalieren jeder Phase unter Verwendung der Summe des berechneten Gesamtvolumenanteils erfüllt. Dies könnte in einem iterativen Prozess kleiner oder größer 1 sein.