流動模型
「流動」(Flow) 模組使用瞬態的納維-斯托克斯方程式可得出質量和動量守恆 H.Ding、F.C. Visser、Y.Jiang 和 M. Furmanczyk,“Demonstration and Validation of a 3-D CFD Simulation Tool Predicting Pump Performance and Cavitation for Industrial Applications”,FEDSM2009-78256,2009。。
雷諾平均納維-斯托克斯方程式 (Reynold’s Averaged Navier-Stokes Equations) 的積分形式 (守恆) 如下所示:
• 連續性
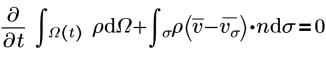
• 動量
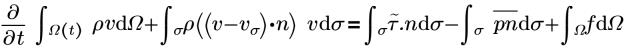
• 應力張量
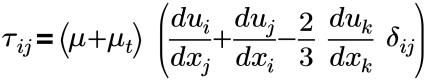
其中,
τij | 有效的剪切應力 (分子 + 亂流) |
f | 主體力 |
n | 曲面法向 |
ρ | 靜態壓力 (Pa) |
t | 時間 |
v | 流體速度 |
vσ | 網格速度 |
Ω(t) | 控制體積塊作為時間函數 |
r | 平均局部流體密度 (kg/m3) |
σ | 控制體積塊的曲面 |
µ | 動態黏度 (Poise 或 Pa-s) |
µt | 亂流的動態黏度 |
δij | Kronecker delta (若 i=j 則等於 1,若 i≠j 則等於 0) |
黏度模型
您可在「恆定動態黏度」(Constant Dynamic Viscosity) 選取項底下的方塊中指定動態黏度的值。
• 「恆定運動黏度」(Constant Kinematic Viscosity) - 在所選的體積塊中指定流體黏度。運動黏度的單位是 m2/s。您可在「恆定運動黏度」(Constant Kinematic Viscosity) 選取項底下的方塊中指定運動黏度的值。
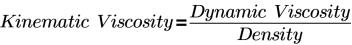
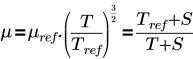
其中,
T | 溫度 (K) |
µ參照 | 處於參照溫度的黏度 (Pa-s) |
S | 蘇哲蘭溫度 (K) |
若是能量模組不在使用中,則需要輸入 T 作為流體溫度 (K)。 |
蘇哲蘭法則 (Sutherland Law) 法則用來計算理想氣體的黏度作為溫度的一個函數。Sutherland, W. (1893),"The viscosity of gases and molecular force",Philosophical Magazine,第 36 頁第 5 段。507-531 (1893). 下表顯示蘇哲蘭對於所選氣體的恆定與參照溫度。參照:en.wikipedia.org/wiki/viscosity。
氣體 | S (K) | Tref (K) | mref (Pa-s) |
|---|---|---|---|
空氣 | 120 | 291.15 | 18.27 e-6 |
氮 | 111 | 300.55 | 17.81 e-6 |
氧 | 127 | 292.25 | 20.81 e-6 |
二氧化碳 | 240 | 293.15 | 14.8 e-6 |
一氧化碳 | 118 | 288.15 | 17.2 e-6 |
氫 | 72 | 293.85 | 8.76 e-6 |
氨 | 370 | 293.15 | 9.82 e-6 |
二氧化硫 | 416 | 293.65 | 12.54 e-6 |
氦 | 79.4 | 273 | 19 e-6 |
非牛頓黏度模型
非牛頓黏度模型如下:
• Herschel-Bulkley 模型
• Bingham 模型
這些模型針對呈現非牛頓流體屬性的各類型流提供適當的黏度。Herschel-Bulkley 模型和 Bingham 模型將剪切應力關聯至剪切速率,如下所示:
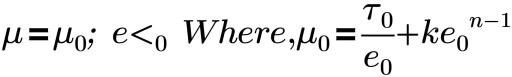
其中,
e0 | 關鍵剪切速率 |
k | 一致性分度 |
τ0 | 流體的屈服應力 |
n | 功率法則分度。針對 Bingham 模型,n=1 |
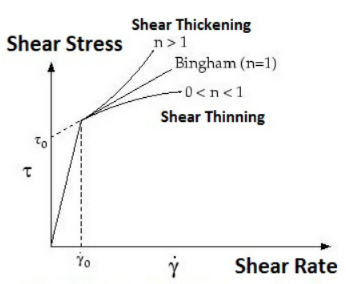
剪切率 0 和上圖中的 gamma 點相同。 |
阻力模型
• 「壓力損失」(Pressure Loss):依據下列方程式:
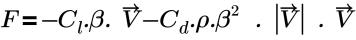
其中,
Cl | 線性拖曳係數 (Pa-s/m2) |
Cd | 二次拖曳係數 (1/m) |
β | 孔隙率 |
ρ | 密度 |
• 「達西法則」(Darcy's Law):模型以下列方程式為基礎:
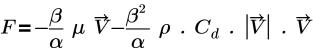
其中,
β | 孔隙率 |
α | 滲透性 |
µ | 動態黏度 |
V | 速度 |
Cd | 二次拖曳係數 (1/m) |
用於阻力方程式中的速度為局部速度。方程式中的 F 使用的量測單位是 N/m3,比如力/體積、壓力梯度 (Dp/Dx) 或 rg。經由將 F 與某個有限的厚度相乘可計算跨介面的壓降。在「一般」(Common) 模組中可設定孔隙率。