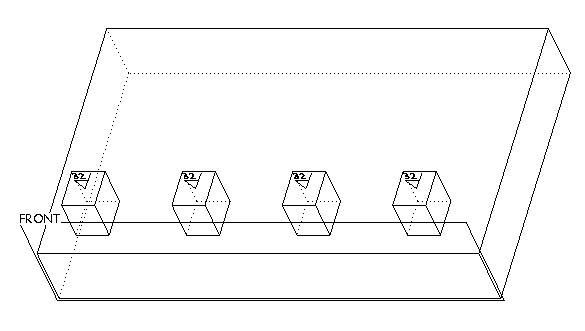
Example: Patterning an Annotation Feature
1. Create an Annotation feature with an Annotation Element of type Surface Finish. Place the Surface Finish symbol on the top plane of the patterned protrusion, as shown in the following illustration.
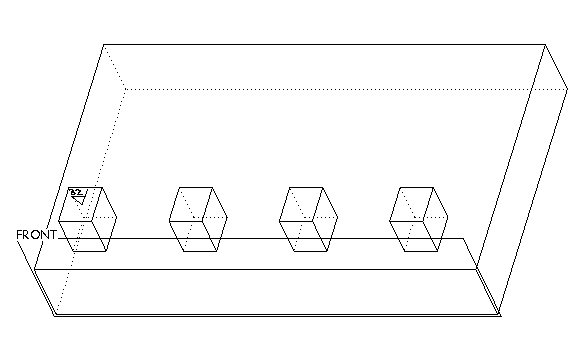
2. Select the Annotation feature in the Model Tree and click  . The system creates a By Reference pattern of the Annotation feature, as shown in the next illustration.
. The system creates a By Reference pattern of the Annotation feature, as shown in the next illustration.
 . The system creates a By Reference pattern of the Annotation feature, as shown in the next illustration.
. The system creates a By Reference pattern of the Annotation feature, as shown in the next illustration.