Моделирование теплопередачи излучением
В тепловых жидкостных системах нагреву или охлаждению путем излучения могут подвергаться твердые поверхности, потоки жидкости или и те и другие. В CFA-моделях теплопередача излучением описывается путем решения уравнения переноса излучением (RTE) с последующим получением члена источника излучения для общего уравнения сохранения энергии. Широко используемый метод моделирования, модель излучения поверхность-поверхность (S2S), является выбранной моделью в Creo Flow Analysis.
Уравнение переноса излучением
Когда луч излучения пересекает слой поглощающего, излучающего и рассеивающего вещества в определенном направлении, луч теряет энергию в результате поглощения и рассеивания. Луч также получает энергию от источников света в среде в результате излучения и рассеивание в направлении луча. Общий баланс энергии в бесконечном слое вещества описывается дифференциальным уравнением, которое называют уравнением переноса излучением (RTE).
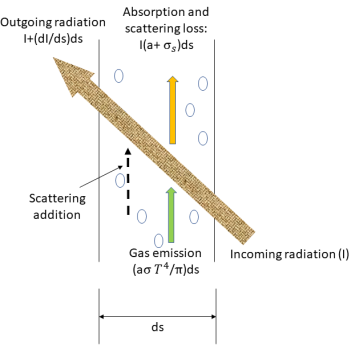
Чтобы вывести уравнение переноса излучением, рассмотрим входящий луч излучения с интенсивностью I, который пересекает вещество, например газ, с инкрементным увеличением плотности ds в направлении 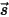 , как показано на рисунке. Падающий в расположении
, как показано на рисунке. Падающий в расположении 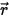 ⃗ и направлении
⃗ и направлении 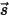 луч, проходя через слой среды, изменяется четырьмя способами, что приводит к увеличению (приобретение энергии, +) или уменьшению (потеря энергии, -) интенсивности излучения
луч, проходя через слой среды, изменяется четырьмя способами, что приводит к увеличению (приобретение энергии, +) или уменьшению (потеря энергии, -) интенсивности излучения 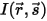 :
:
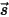 , как показано на рисунке. Падающий в расположении
, как показано на рисунке. Падающий в расположении 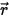 ⃗ и направлении
⃗ и направлении 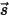 луч, проходя через слой среды, изменяется четырьмя способами, что приводит к увеличению (приобретение энергии, +) или уменьшению (потеря энергии, -) интенсивности излучения
луч, проходя через слой среды, изменяется четырьмя способами, что приводит к увеличению (приобретение энергии, +) или уменьшению (потеря энергии, -) интенсивности излучения 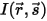 :
:• Поглощение - среда, например газ, поглощает часть проходящего излучения. С коэффициентом поглощения 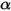 потеря энергии излучения при поглощении имеет вид:
потеря энергии излучения при поглощении имеет вид:
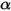 потеря энергии излучения при поглощении имеет вид:
потеря энергии излучения при поглощении имеет вид: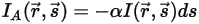
Уравнение 2.282
• Рассеивание - среда, например газ, рассеивает часть энергии излучения в другом направлении (отличном от направления 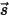 ), когда луч проходит через среду. С коэффициентом рассеивания
), когда луч проходит через среду. С коэффициентом рассеивания 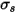 энергия, теряемая при рассеивании, имеет вид:
энергия, теряемая при рассеивании, имеет вид:
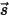 ), когда луч проходит через среду. С коэффициентом рассеивания
), когда луч проходит через среду. С коэффициентом рассеивания 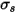 энергия, теряемая при рассеивании, имеет вид:
энергия, теряемая при рассеивании, имеет вид: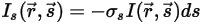
Уравнение 2.283
• Эмиссия - среда испускает энергию излучения в луч как серое тело в соответствии с ее локальной температурой (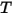 ) и эмиссионными характеристиками. На основе закона Стефана - Больцмана и взаимности между излучением и поглощением, уравнения 2.274 и уравнения 2.279, интенсивность излучения среды имеет вид:
) и эмиссионными характеристиками. На основе закона Стефана - Больцмана и взаимности между излучением и поглощением, уравнения 2.274 и уравнения 2.279, интенсивность излучения среды имеет вид: 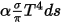
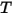 ) и эмиссионными характеристиками. На основе закона Стефана - Больцмана и взаимности между излучением и поглощением, уравнения 2.274 и уравнения 2.279, интенсивность излучения среды имеет вид:
) и эмиссионными характеристиками. На основе закона Стефана - Больцмана и взаимности между излучением и поглощением, уравнения 2.274 и уравнения 2.279, интенсивность излучения среды имеет вид: 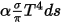
Кроме того, если предположить, что n является коэффициентом преломления среды, который определяется как отношение скорости света в вакууме к его скорости в указанной среде, то фактическая приобретенная лучом энергия излучения имеет вид:
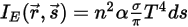
Уравнение 2.284
• Рассеивание другого излучения - часть излучения от других источников в слое вещества рассеивается в направлении луча излучения в зависимости от векторов положения и направления 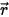 и
и 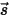 . С введением
. С введением 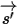
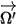 для представления направления и телесного угла излучения, а также
для представления направления и телесного угла излучения, а также 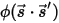 для функции фазы получаем долю интенсивности лучей, идущих во всех направлениях, которая рассеивается в направление
для функции фазы получаем долю интенсивности лучей, идущих во всех направлениях, которая рассеивается в направление 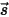 ⃗в виде:
⃗в виде:
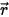 и
и 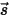 . С введением
. С введением 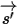
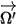 для представления направления и телесного угла излучения, а также
для представления направления и телесного угла излучения, а также 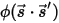 для функции фазы получаем долю интенсивности лучей, идущих во всех направлениях, которая рассеивается в направление
для функции фазы получаем долю интенсивности лучей, идущих во всех направлениях, которая рассеивается в направление 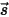 ⃗в виде:
⃗в виде: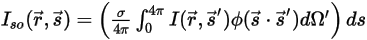
Уравнение 2.285
Отметим, что в уравнении 2.285 процессы рассеивания игнорируются.
Для падающего излучения 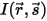 и выходящего излучения
и выходящего излучения 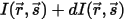 баланс энергии излучения в направлении
баланс энергии излучения в направлении 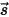 ⃗ имеет вид:
⃗ имеет вид:
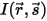 и выходящего излучения
и выходящего излучения 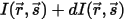 баланс энергии излучения в направлении
баланс энергии излучения в направлении 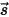 ⃗ имеет вид:
⃗ имеет вид: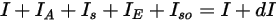
Уравнение 2.286
Подстановка уравнений 2.282 - 2.285 в уравнение 2.286 после деления на 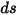 дает уравнение переноса излучением (RTE) в следующем виде:
дает уравнение переноса излучением (RTE) в следующем виде:
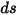 дает уравнение переноса излучением (RTE) в следующем виде:
дает уравнение переноса излучением (RTE) в следующем виде: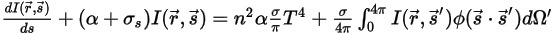
Уравнение 2.287
RTE является интегро-дифференциальным уравнением первого порядка для интенсивности излучения 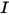 в заданном направлении
в заданном направлении 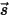 . Чтобы решить это уравнение в области, необходимо знать температурное поле в области. Кроме того, требуются граничные условия для
. Чтобы решить это уравнение в области, необходимо знать температурное поле в области. Кроме того, требуются граничные условия для 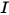 на внутренних и внешних поверхностях, а также на поверхностях раздела между различными средами.
на внутренних и внешних поверхностях, а также на поверхностях раздела между различными средами.
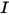 в заданном направлении
в заданном направлении 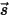 . Чтобы решить это уравнение в области, необходимо знать температурное поле в области. Кроме того, требуются граничные условия для
. Чтобы решить это уравнение в области, необходимо знать температурное поле в области. Кроме того, требуются граничные условия для 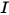 на внутренних и внешних поверхностях, а также на поверхностях раздела между различными средами.
на внутренних и внешних поверхностях, а также на поверхностях раздела между различными средами.Локальную среднюю температуру получаем из решения для уравнения сохранения полной энергии (включая источники излучения), которое описано в модуле Теплота (Heat). Однако для теплового излучения обработка границ является сложной и зависит от моделей излучения. В целом граница может быть непрозрачной средой, которая испускает, отражает и поглощает, либо полупрозрачной средой, которая к тому же пропускает излучение. Отражение и пропускание могут быть диффузным и/или зеркальным. Например, на испускающей и отражающей непрозрачной границе с серым излучением, а также в зависимости от типа отражения интенсивность луча может быть выражена следующим образом:
◦ Непрозрачная граница с диффузным испусканием и отражением:
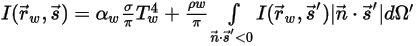
Уравнение 2.288
◦ Непрозрачная граница с испусканием и зеркальным отражением:
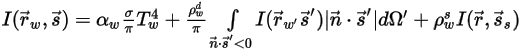
Уравнение 2.289
Здесь
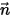 ⃗ ⃗ | единичный вектор нормали к поверхности в положении 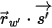 |
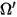 | направление и телесный угол диффузно отраженного луча (равномерное отражение во всех направлениях) |
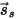 | направление зеркально отраженного луча (идеальное отражение в зависимости от угла падения) |
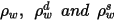 | отражающая способность поверхности, диффузное отражение и зеркальное отражение, соответственно, имеющие следующую взаимосвязь: 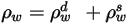 Уравнение 2.290 |
При заданных граничных условиях уравнение 2.287 определяет передачу интенсивности излучения в указанном направлении. Для серого излучения уравнение 2.287 должно решаться для всех направлений внутри сферы. Для несерого излучения интенсивность также зависит от длины волны. Таким образом, уравнение должно решаться для всех направлений по всему спектру длин волн. Очевидно, прямое решение уравнения переноса излучением занимает очень много времени. Поэтому в большинстве инженерных расчетов для учета направлений и спектральной зависимости желательно использовать некоторые упрощенные, но дающие хорошее приближение модели. В CFD-расчетах обычно применяются следующие модели излучения, подробное описание которых можно найти по ссылкам.
Ссылки: R. Siegel and J. R. Howell, Thermal Radiation Heat Transfer (Модель излучения Росселанда. "Теплопередача тепловым излучением"), Hemisphere Publishing Corporation, Washington DC, 1992 (на английском языке).
▪ Модель излучения Росселанда
Ссылки: R. Siegel and J. R. Howell, Thermal Radiation Heat Transfer (Теплопередача тепловым излучением), Hemisphere Publishing Corporation, Washington DC, 1992 (на английском языке).
▪ Модель излучения P-1
Ссылки: R. Siegel and J. R. Howell, Thermal Radiation Heat Transfer (Теплопередача тепловым излучением), Hemisphere Publishing Corporation, Washington DC, 1992 (на английском языке).
▪ Модель излучения дискретным переносом
Ссылки: N. G. Shah, A New Method of Computation of Radiant Heat Transfer in Combustion Chambers” (Новый метод расчета теплопередачи излучения в камерах сгорания), PhD thesis, Imperial College of Science and Technology, London, England, 1979. (на английском языке).
Ссылки: M. G. Carvalho, T. Farias, and P. Fontes, "Predicting Radiative Heat Transfer in Absorbing, Emitting, and Scattering Media Using the Discrete Transfer Method" (Прогнозирование радиационного теплообмена в поглощающих, излучающих и рассеивающих средах с использованием метода дискретного переноса), In W. A. Fiveland et al., editor, Fundamentals of Radiation Heat Transfer, volume 160, pages 17-26. ASME ХТД, 1991. (Дискретная модель передачи излучением. "Предсказание теплопередачи излучением в поглощающей, излучающей и рассеивающей среде с помощью дискретного метода переноса", в сб. "Основы радиационного теплопереноса", т. 160, с. 17-26.)
▪ Модель излучения поверхность-поверхность (S2S)
Ссылки: R. Siegel and J. R. Howell, Thermal Radiation Heat Transfer (Модель излучения Росселанда. "Теплопередача тепловым излучением"), Hemisphere Publishing Corporation, Washington DC, 1992 (на английском языке).
▪ Модель излучения с дискретными ординатами (DO)
Ссылки: G. D. Raithby and E. H. Chui, "A Finite-Volume Method for Predicting a Radiant Heat Transfer in Enclosures with Participating Media" (Модель излучения с дискретными ординатами. "Метод конечного объема для прогнозирования теплопередачи излучением в замкнутых объемах с участием вещества"), J. Heat Transfer, 112:415-423, 1990. (на английском языке).
Ссылки: E. H. Chui and G. D. Raithby, "Computation of Radiant Heat Transfer on a Non-Orthogonal Mesh Using the Finite-Volume Method" (Расчет теплопередачи излучением на неортогональной сетке с помощью метода конечного объема), Numerical Heat Transfer, Part B, 23:269-288, 1993. (на английском языке).
Каждая модель имеет свои собственные преимущества и ограничения по точности и затратам. Например, в модели Росселанда не решается уравнение переноса для падающего излучения, но это самая быстрая модель излучения, для которой требуется минимум дополнительной памяти. Модель Росселанда может использоваться только для оптически толстой (оптическая толщина - это натуральный логарифм отношения мощности падающего излучения к мощности излучения, прошедшего через среду) среды из-за чрезмерного упрощения уравнения переноса излучением.
В модели излучения с дискретными ординатами (DO) уравнение 2.287 преобразуется в уравнение переноса для интенсивности излучения в пространственных координатах 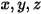 , которое решается на конечном числе дискретных телесных углов, связанных с направлением вектора
, которое решается на конечном числе дискретных телесных углов, связанных с направлением вектора 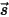 . Число выбранных телесных углов непосредственно определяет точность и затраты на вычисления. Метод моделирования DO также идентичен методу, который используется для уравнений потока и энергии жидкости. В настоящее время это наиболее общая модель излучения, которая охватывает весь диапазон оптических толщин и может применяться к проблемам от излучения с поверхности на поверхность до процессов с участием излучения, таким как система сгорания. Однако затраты на расчеты в модели DO высоки для несерого излучения.
. Число выбранных телесных углов непосредственно определяет точность и затраты на вычисления. Метод моделирования DO также идентичен методу, который используется для уравнений потока и энергии жидкости. В настоящее время это наиболее общая модель излучения, которая охватывает весь диапазон оптических толщин и может применяться к проблемам от излучения с поверхности на поверхность до процессов с участием излучения, таким как система сгорания. Однако затраты на расчеты в модели DO высоки для несерого излучения.
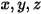 , которое решается на конечном числе дискретных телесных углов, связанных с направлением вектора
, которое решается на конечном числе дискретных телесных углов, связанных с направлением вектора 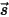 . Число выбранных телесных углов непосредственно определяет точность и затраты на вычисления. Метод моделирования DO также идентичен методу, который используется для уравнений потока и энергии жидкости. В настоящее время это наиболее общая модель излучения, которая охватывает весь диапазон оптических толщин и может применяться к проблемам от излучения с поверхности на поверхность до процессов с участием излучения, таким как система сгорания. Однако затраты на расчеты в модели DO высоки для несерого излучения.
. Число выбранных телесных углов непосредственно определяет точность и затраты на вычисления. Метод моделирования DO также идентичен методу, который используется для уравнений потока и энергии жидкости. В настоящее время это наиболее общая модель излучения, которая охватывает весь диапазон оптических толщин и может применяться к проблемам от излучения с поверхности на поверхность до процессов с участием излучения, таким как система сгорания. Однако затраты на расчеты в модели DO высоки для несерого излучения.Среди перечисленных выше моделей излучения модель излучения поверхность-поверхность (S2S) особенно подходит для моделирования передачи излучением в замкнутых объемах без учета участия среды. Типичными примерами являются пространственные излучающие нагреватели, а также подкапотные и кузовные автомобильные системы. В таких ситуациях модели излучения для участвующего излучения иногда являются неэффективными. По сравнению с моделью излучения DO в модели S2S итерации выполняются быстрее, хотя расчет коэффициента вида может привести к большой нагрузке на ЦП. В Creo Flow Analysis текущим выбором модели для теплопередачи излучения является модель излучения S2S.
Модель излучения поверхность-поверхность (S2S)
Модель излучения поверхность-поверхность описывает обмен энергией излучения в закрытом объеме с серыми диффузными поверхностями без участия среды. Обмен энергией излучения между поверхностями зависит от двух основных факторов: характеристики излучения участвующих поверхностей и геометрические параметры, в том числе площади и формы поверхностей, а также их относительное расположение(расстояние и ориентация). В модели излучения S2S теплопередача излучением с поверхности рассматривается в модели серого диффузного излучения, тогда как геометрические параметры учитываются с помощью геометрической функции, которую называют коэффициентом вида.
• Серое диффузное излучение
В модели излучения S2S предполагается, что поверхности являются серыми и диффузными (серое излучение). Для серой поверхности обе величины, излучающая способность (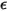 ) и поглощающая способность (
) и поглощающая способность (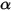 ) поверхностей, не зависят от длин волн испускаемого и поглощаемого излучения. Согласно закону Кирхгофа для теплового излучения, в уравнении 2.274 излучающая способность равна поглощающей способности:
) поверхностей, не зависят от длин волн испускаемого и поглощаемого излучения. Согласно закону Кирхгофа для теплового излучения, в уравнении 2.274 излучающая способность равна поглощающей способности:
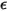 ) и поглощающая способность (
) и поглощающая способность (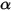 ) поверхностей, не зависят от длин волн испускаемого и поглощаемого излучения. Согласно закону Кирхгофа для теплового излучения, в уравнении 2.274 излучающая способность равна поглощающей способности:
) поверхностей, не зависят от длин волн испускаемого и поглощаемого излучения. Согласно закону Кирхгофа для теплового излучения, в уравнении 2.274 излучающая способность равна поглощающей способности: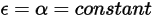
Уравнение 2.291
Кроме того, в предположении диффузной поверхности зеркальное отражение отсутствует, а отражающая способность (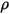 ) для падающего излучения на поверхности считается изотропной относительно телесного угла. В уравнении 2.290 отражающая способность поверхности определяется как:
) для падающего излучения на поверхности считается изотропной относительно телесного угла. В уравнении 2.290 отражающая способность поверхности определяется как:
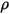 ) для падающего излучения на поверхности считается изотропной относительно телесного угла. В уравнении 2.290 отражающая способность поверхности определяется как:
) для падающего излучения на поверхности считается изотропной относительно телесного угла. В уравнении 2.290 отражающая способность поверхности определяется как: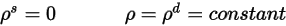
Уравнение 2.292
Здесь
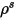 | зеркальное отражение |
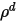 | диффузное отражение |
Для непрозрачной или полупрозрачной поверхности коэффициент пропускания 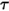 также не зависит от длины волны:
также не зависит от длины волны:
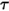 также не зависит от длины волны:
также не зависит от длины волны: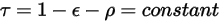
Уравнение 2.293
В модели серой диффузной поверхности предполагается, что на обмен энергией излучения между поверхностями практически не влияет разделяющая их среда. Таким образом, если на единицу площади поверхности падает определенная величина энергии излучения 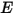 (облучение), то отражаемыми, поглощаемыми и пропускаемыми долями энергии излучения являются
(облучение), то отражаемыми, поглощаемыми и пропускаемыми долями энергии излучения являются 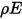 ,
, 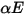 и
и 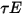 соответственно. Поскольку в большинстве случаев применения поверхности являются непрозрачными для теплового излучения в инфракрасном спектре, излучающие поверхности в дальнейшем могут считаться непрозрачными. Таким образом, коэффициентом пропускания можно пренебрегать
соответственно. Поскольку в большинстве случаев применения поверхности являются непрозрачными для теплового излучения в инфракрасном спектре, излучающие поверхности в дальнейшем могут считаться непрозрачными. Таким образом, коэффициентом пропускания можно пренебрегать 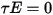 . В уравнениях 2.273 и 2.274 отражающая способность поверхности
. В уравнениях 2.273 и 2.274 отражающая способность поверхности 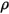 выражается как:
выражается как:
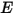 (облучение), то отражаемыми, поглощаемыми и пропускаемыми долями энергии излучения являются
(облучение), то отражаемыми, поглощаемыми и пропускаемыми долями энергии излучения являются 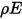 ,
, 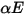 и
и 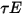 соответственно. Поскольку в большинстве случаев применения поверхности являются непрозрачными для теплового излучения в инфракрасном спектре, излучающие поверхности в дальнейшем могут считаться непрозрачными. Таким образом, коэффициентом пропускания можно пренебрегать
соответственно. Поскольку в большинстве случаев применения поверхности являются непрозрачными для теплового излучения в инфракрасном спектре, излучающие поверхности в дальнейшем могут считаться непрозрачными. Таким образом, коэффициентом пропускания можно пренебрегать 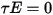 . В уравнениях 2.273 и 2.274 отражающая способность поверхности
. В уравнениях 2.273 и 2.274 отражающая способность поверхности 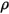 выражается как:
выражается как: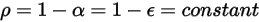
Уравнение 2.294
В предположении серого диффузного излучения поверхности уравнение моделирования S2S строится на основе сохранения энергии на каждой поверхности.
• Уравнение моделирования S2S
Основным предположением модели S2S является то, что в замкнутой системе теплопередача излучением имеет место только между серыми диффузными поверхностями (серое излучение). В среде, разделяющей поверхности, можно игнорировать поглощение, излучение или рассеяние излучения. Поэтому для численного анализа учитывается только излучение поверхность-поверхность.
Поток энергии излучения, выходящий с данной поверхности, состоит из непосредственно испускаемой и отраженной энергии. Поток отраженной энергии зависит от потока падающей энергии, который можно выразить через поток энергии, испускаемый всеми остальными поверхностями. Чтобы рассчитать поток энергии излучения на поверхности, удобно определить энергетическую светимость 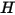 , которая является суммой мощности излучения на единицу площади (эмиттанс)
, которая является суммой мощности излучения на единицу площади (эмиттанс) 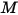 и отраженной частью мощности излучения, принимаемого поверхностью на единицу площади (облученность)
и отраженной частью мощности излучения, принимаемого поверхностью на единицу площади (облученность) 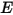 :
:
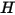 , которая является суммой мощности излучения на единицу площади (эмиттанс)
, которая является суммой мощности излучения на единицу площади (эмиттанс) 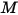 и отраженной частью мощности излучения, принимаемого поверхностью на единицу площади (облученность)
и отраженной частью мощности излучения, принимаемого поверхностью на единицу площади (облученность) 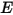 :
: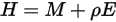
Уравнение 2.295
Для непрозрачной поверхности 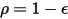 имеется энергетическая светимость:
имеется энергетическая светимость:
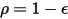 имеется энергетическая светимость:
имеется энергетическая светимость: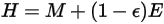
Уравнение 2.296
С допущениями в модели S2S, таким образом, можно сформулировать следующую систему линейных уравнений для расчета энергетической светимости каждой поверхности в замкнутой системе. В предположении, что 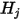 представляет энергетическую светимость на произвольной поверхности
представляет энергетическую светимость на произвольной поверхности 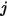 ,
, 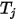 является температурой поверхности, а
является температурой поверхности, а 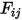 является коэффициентом вида между поверхностью
является коэффициентом вида между поверхностью 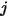 и
и  , мы имеем энергетическую светимость поверхности
, мы имеем энергетическую светимость поверхности  :
:
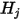 представляет энергетическую светимость на произвольной поверхности
представляет энергетическую светимость на произвольной поверхности 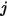 ,
, 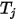 является температурой поверхности, а
является температурой поверхности, а 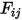 является коэффициентом вида между поверхностью
является коэффициентом вида между поверхностью 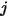 и
и  , мы имеем энергетическую светимость поверхности
, мы имеем энергетическую светимость поверхности  :
: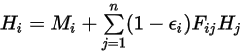
Уравнение 2.297
Здесь 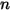 - число поверхностей, участвующих в теплопередаче излучением. После введения символа Кронекера
- число поверхностей, участвующих в теплопередаче излучением. После введения символа Кронекера 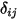 и применения закона Стефана - Больцмана для серого излучения, уравнение 2.278, можно преобразовать уравнение 2.297 и вывести уравнение моделирования S2S:
и применения закона Стефана - Больцмана для серого излучения, уравнение 2.278, можно преобразовать уравнение 2.297 и вывести уравнение моделирования S2S:
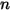 - число поверхностей, участвующих в теплопередаче излучением. После введения символа Кронекера
- число поверхностей, участвующих в теплопередаче излучением. После введения символа Кронекера 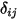 и применения закона Стефана - Больцмана для серого излучения, уравнение 2.278, можно преобразовать уравнение 2.297 и вывести уравнение моделирования S2S:
и применения закона Стефана - Больцмана для серого излучения, уравнение 2.278, можно преобразовать уравнение 2.297 и вывести уравнение моделирования S2S: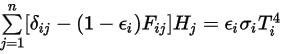
Уравнение 2.298
С предварительно рассчитанным коэффициентом вида 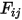 система линейных уравнений 2.298 решается, чтобы получить
система линейных уравнений 2.298 решается, чтобы получить 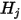 для участвующих поверхностей. Затем легко вычисляются тепловые потоки излучения на каждой поверхности. Для поверхности
для участвующих поверхностей. Затем легко вычисляются тепловые потоки излучения на каждой поверхности. Для поверхности  результирующий тепловой поток излучения
результирующий тепловой поток излучения 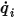 является разностью между испускаемым (
является разностью между испускаемым (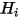 ) и падающим (
) и падающим (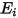 ) излучением на единицу площади. Из уравнений 2.278 и 2.296 можно вывести следующую формулу для потока:
) излучением на единицу площади. Из уравнений 2.278 и 2.296 можно вывести следующую формулу для потока:
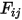 система линейных уравнений 2.298 решается, чтобы получить
система линейных уравнений 2.298 решается, чтобы получить 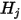 для участвующих поверхностей. Затем легко вычисляются тепловые потоки излучения на каждой поверхности. Для поверхности
для участвующих поверхностей. Затем легко вычисляются тепловые потоки излучения на каждой поверхности. Для поверхности  результирующий тепловой поток излучения
результирующий тепловой поток излучения 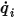 является разностью между испускаемым (
является разностью между испускаемым (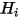 ) и падающим (
) и падающим (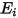 ) излучением на единицу площади. Из уравнений 2.278 и 2.296 можно вывести следующую формулу для потока:
) излучением на единицу площади. Из уравнений 2.278 и 2.296 можно вывести следующую формулу для потока: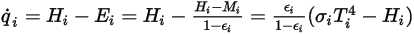
Уравнение 2.299
Для данной области поверхности 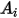 результирующие тепловые потоки излучения, испускаемые поверхностью
результирующие тепловые потоки излучения, испускаемые поверхностью 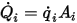 , рассчитываются как:
, рассчитываются как:
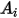 результирующие тепловые потоки излучения, испускаемые поверхностью
результирующие тепловые потоки излучения, испускаемые поверхностью 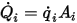 , рассчитываются как:
, рассчитываются как: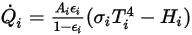
Уравнение 2.300
Модель S2S состоит из системы линейных уравнений в форме уравнения 2.298. Преимуществом модели является то, что для заданных коэффициентов вида и температур расчет результирующих тепловых потоков выполняется путем решения системы линейных уравнений, которые решаются путем применения численных алгоритмов. Однако главной сложностью в применении предполагаемой модели поверхность-поверхность является расчет коэффициентов вида 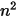 для числа n участвующих поверхностей. Это может занять много времени, особенно при увеличении числа поверхностей.
для числа n участвующих поверхностей. Это может занять много времени, особенно при увеличении числа поверхностей.
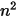 для числа n участвующих поверхностей. Это может занять много времени, особенно при увеличении числа поверхностей.
для числа n участвующих поверхностей. Это может занять много времени, особенно при увеличении числа поверхностей.Расчет коэффициента вида
В уравнении моделирования S2S 2.298коэффициент вида 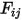 представляет пропорцию излучения, которая испускается поверхностью
представляет пропорцию излучения, которая испускается поверхностью  и падает на поверхность
и падает на поверхность 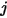 . Как показано на рис. 2.37, в предположение, что
. Как показано на рис. 2.37, в предположение, что 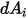 - это дифференциальная площадь на поверхности
- это дифференциальная площадь на поверхности  ,
, 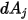 - дифференциальная площадь на поверхности
- дифференциальная площадь на поверхности 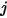 , а расстояние между
, а расстояние между 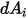 и
и 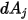 равно
равно 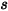 , коэффициент вида
, коэффициент вида 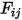 от
от 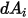 до
до 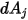 на расстоянии
на расстоянии 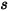 можно выразить следующим образом:
можно выразить следующим образом:
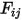 представляет пропорцию излучения, которая испускается поверхностью
представляет пропорцию излучения, которая испускается поверхностью  и падает на поверхность
и падает на поверхность 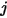 . Как показано на рис. 2.37, в предположение, что
. Как показано на рис. 2.37, в предположение, что 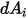 - это дифференциальная площадь на поверхности
- это дифференциальная площадь на поверхности  ,
, 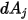 - дифференциальная площадь на поверхности
- дифференциальная площадь на поверхности 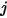 , а расстояние между
, а расстояние между 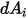 и
и 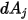 равно
равно 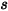 , коэффициент вида
, коэффициент вида 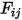 от
от 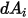 до
до 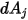 на расстоянии
на расстоянии 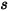 можно выразить следующим образом:
можно выразить следующим образом: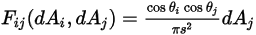
Уравнение 2.301
Здесь 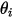 и
и 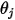 - это угол между направлениями нормали к поверхности и лучом между двумя дифференциальными областями.
- это угол между направлениями нормали к поверхности и лучом между двумя дифференциальными областями.
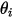 и
и 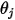 - это угол между направлениями нормали к поверхности и лучом между двумя дифференциальными областями.
- это угол между направлениями нормали к поверхности и лучом между двумя дифференциальными областями.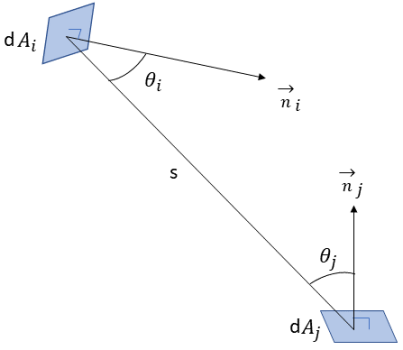
Рис. 2.37
Если 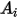 и
и 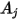 являются заданными областями поверхности
являются заданными областями поверхности  и
и 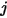 соответственно, коэффициент вида от поверхности
соответственно, коэффициент вида от поверхности  к поверхности
к поверхности 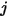 является усредненным интегралом по площади уравнения 2.301 на поверхности
является усредненным интегралом по площади уравнения 2.301 на поверхности  и
и 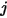 :
:
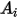 и
и 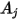 являются заданными областями поверхности
являются заданными областями поверхности  и
и 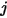 соответственно, коэффициент вида от поверхности
соответственно, коэффициент вида от поверхности  к поверхности
к поверхности 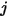 является усредненным интегралом по площади уравнения 2.301 на поверхности
является усредненным интегралом по площади уравнения 2.301 на поверхности  и
и 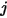 :
: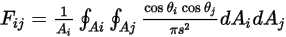
Уравнение 2.302
Отметим, что излучение поверхность-поверхность имеет место только в том случае, если две поверхности являются видимыми друг для друга или если коэффициент вида не равен нулю. Введение символа Кронекера 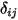 для видимости между
для видимости между 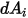 и
и 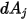 :
:
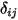 для видимости между
для видимости между 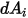 и
и 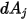 :
: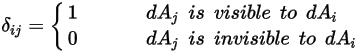
Уравнение 2.303
Уравнение 2.302 можно переписать как:
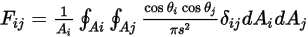
Уравнение 2.304
Для любых двух поверхностей, видимых друг для друга, заданная поверхность  излучает только часть исходящей энергии излучения на поверхность
излучает только часть исходящей энергии излучения на поверхность 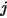 , как показано на рис. 2.378. Таким образом, безразмерный коэффициент вида
, как показано на рис. 2.378. Таким образом, безразмерный коэффициент вида 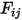 представляет часть энергии, которая выходит с поверхности
представляет часть энергии, которая выходит с поверхности  и попадает на поверхность
и попадает на поверхность 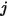 . Характеристики представлены в следующем списке:
. Характеристики представлены в следующем списке:
 излучает только часть исходящей энергии излучения на поверхность
излучает только часть исходящей энергии излучения на поверхность 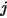 , как показано на рис. 2.378. Таким образом, безразмерный коэффициент вида
, как показано на рис. 2.378. Таким образом, безразмерный коэффициент вида 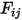 представляет часть энергии, которая выходит с поверхности
представляет часть энергии, которая выходит с поверхности  и попадает на поверхность
и попадает на поверхность 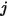 . Характеристики представлены в следующем списке:
. Характеристики представлены в следующем списке: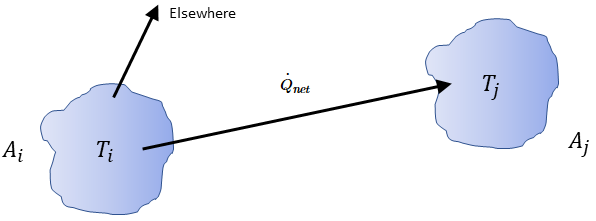
Рис. 2.378
• Суммирование коэффициентов вида - поскольку излучение, выходящее с поверхности, сохраняется, сумма всех коэффициентов вида с данной поверхности  равняется единице. Для системы с замкнутой поверхностью
равняется единице. Для системы с замкнутой поверхностью 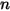 имеем:
имеем:
 равняется единице. Для системы с замкнутой поверхностью
равняется единице. Для системы с замкнутой поверхностью 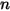 имеем:
имеем:
Уравнение 2.305
• Видящие себя поверхности - так как излучение передается прямолинейными лучами, ни один луч, выходящий с выпуклой поверхности, не может попасть на ту же поверхность. Следовательно, выпуклые поверхности не могут быть видящими себя.
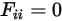
Уравнение 2.306
Для вогнутых поверхностей луч, исходящий из одного места поверхности, может попасть в другое место той же поверхности. Поэтому вогнутая поверхность может быть видящей себя:
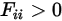
Уравнение 2.307
• Суперпозиция - для системы с поверхностью 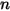 , если данная поверхность
, если данная поверхность  излучает на
излучает на 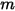 поверхностей (
поверхностей (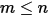 ), то коэффициент вида между поверхностью
), то коэффициент вида между поверхностью  и числом поверхностей
и числом поверхностей 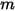 равняется сумме коэффициентов вида между поверхностью
равняется сумме коэффициентов вида между поверхностью  и каждой из
и каждой из 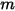 поверхностей:
поверхностей:
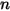 , если данная поверхность
, если данная поверхность  излучает на
излучает на 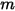 поверхностей (
поверхностей (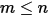 ), то коэффициент вида между поверхностью
), то коэффициент вида между поверхностью  и числом поверхностей
и числом поверхностей 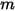 равняется сумме коэффициентов вида между поверхностью
равняется сумме коэффициентов вида между поверхностью  и каждой из
и каждой из 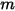 поверхностей:
поверхностей: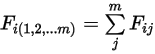
Уравнение 2.308
Правило суперпозиции или правило суммирования полезно, когда недоступна геометрия с заданными диаграммами или графиками. Правило суперпозиции позволяет выразить искомую геометрию, используя сумму или разность известных геометрических объектов.
• Взаимность - уравнение 2.304 определяет коэффициент вида 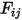 как долю энергии излучения, которая выходит с поверхности
как долю энергии излучения, которая выходит с поверхности  и попадает на поверхность
и попадает на поверхность 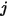 . Аналогично коэффициент вида
. Аналогично коэффициент вида 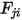 , представляющий часть энергии, которая выходит с поверхности
, представляющий часть энергии, которая выходит с поверхности 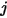 и попадает на поверхность
и попадает на поверхность  , выражается следующим образом:
, выражается следующим образом:
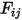 как долю энергии излучения, которая выходит с поверхности
как долю энергии излучения, которая выходит с поверхности  и попадает на поверхность
и попадает на поверхность 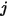 . Аналогично коэффициент вида
. Аналогично коэффициент вида 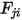 , представляющий часть энергии, которая выходит с поверхности
, представляющий часть энергии, которая выходит с поверхности 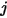 и попадает на поверхность
и попадает на поверхность  , выражается следующим образом:
, выражается следующим образом: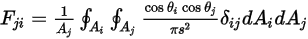
Уравнение 2.309
Если сравнить уравнение 2.309 с уравнением 2.304, получим следующую взаимосвязь:
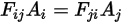
Уравнение 2.310
Уравнение 2.310 называют взаимностью коэффициентов вида. Теорема взаимности позволяет непосредственно рассчитывать только одну пару коэффициентов вида.
Кластеризация
Для модели излучения S2S требуются большие вычислительные мощности, если число излучающих поверхностей велико. Чтобы сократить время расчета и требования к памяти, можно уменьшить число излучающих поверхностей, группируя несколько соседних граней граничных ячеек для создания поверхностных кластеров. Затем расчет энергетической светимости (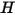 ) выполняется для поверхностных кластеров. Потом эти значения распространяются на грани граничных ячеек в пределах каждого кластера для расчета температур стенки. Так как выражения для источников излучения имеют высокую степень нелинейности (пропорциональность четвертой степени температуры), необходимо правильно рассчитывать среднюю температуру поверхностных кластеров и правильно распределять выражения для потоков и источников между граничными гранями, которые образуют кластеры.
) выполняется для поверхностных кластеров. Потом эти значения распространяются на грани граничных ячеек в пределах каждого кластера для расчета температур стенки. Так как выражения для источников излучения имеют высокую степень нелинейности (пропорциональность четвертой степени температуры), необходимо правильно рассчитывать среднюю температуру поверхностных кластеров и правильно распределять выражения для потоков и источников между граничными гранями, которые образуют кластеры.
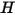 ) выполняется для поверхностных кластеров. Потом эти значения распространяются на грани граничных ячеек в пределах каждого кластера для расчета температур стенки. Так как выражения для источников излучения имеют высокую степень нелинейности (пропорциональность четвертой степени температуры), необходимо правильно рассчитывать среднюю температуру поверхностных кластеров и правильно распределять выражения для потоков и источников между граничными гранями, которые образуют кластеры.
) выполняется для поверхностных кластеров. Потом эти значения распространяются на грани граничных ячеек в пределах каждого кластера для расчета температур стенки. Так как выражения для источников излучения имеют высокую степень нелинейности (пропорциональность четвертой степени температуры), необходимо правильно рассчитывать среднюю температуру поверхностных кластеров и правильно распределять выражения для потоков и источников между граничными гранями, которые образуют кластеры.Температуру поверхности кластера получаем путем усреднения температуры граничных граней, как показано в следующем уравнении:
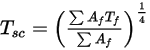
Уравнение 2.311
Здесь 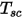 - температура поверхностного кластера, а
- температура поверхностного кластера, а 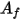 и
и 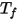 - площадь грани и температура граничной ячейки в CFA-моделировании. Суммирование выполнятся по всем граням в поверхностном кластере.
- площадь грани и температура граничной ячейки в CFA-моделировании. Суммирование выполнятся по всем граням в поверхностном кластере.
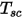 - температура поверхностного кластера, а
- температура поверхностного кластера, а 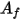 и
и 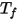 - площадь грани и температура граничной ячейки в CFA-моделировании. Суммирование выполнятся по всем граням в поверхностном кластере.
- площадь грани и температура граничной ячейки в CFA-моделировании. Суммирование выполнятся по всем граням в поверхностном кластере.