Решатель ОДУ
Обыкновенные дифференциальные уравнения (ОДУ) уравнение 2.432 и уравнение 2.444, которые описывают перемещение и вращение с одной степенью свободы границ и объемов, соответственно, решаются в Creo Flow Analysis численно. В частности, чтобы рассчитать движение и смещение границы и объема для пересчета сетки, следует принять следующие схемы шагов по времени, чтобы интегрировать ОДУ: решатель жестких систем, явный решатель Эйлера и явный решатель Рунге - Кутты.
Интегрирование уравнения движения с одной степенью свободы
Подстановка уравнения 2.434, уравнения 2.435 и уравнения 2.436 в уравнение 2.432 и явная группировка сил в единый член,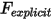 
для краткости, позволяет переписать уравнение перемещения с одной степенью свободы в следующей форме:
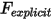для краткости, позволяет переписать уравнение перемещения с одной степенью свободы в следующей форме: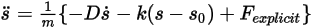
Уравнение 2.455
Здесь явно вычисляемый член силы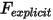 
имеет вид:
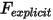имеет вид: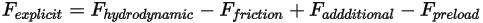
Уравнение 2.456
С заданными начальными и граничными условиями смещение твердого тела получается интегрированием уравнения 2.455 с использованием явных схем шагов по времени. В зависимости от шага времени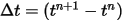 
общие формулы имеют следующий вид:
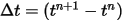общие формулы имеют следующий вид: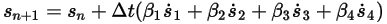
Уравнение 2.457
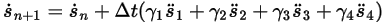
Уравнение 2.458
Здесь сумма весовых коэффициентов равна единице:
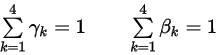
Уравнение 2.459
При выборе весовых коэффициентов выводятся различные схемы. Например, явные схемы Эйлера и Рунге - Кутты:
• Явный решатель Эйлера (1-го порядка)
С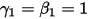 
и 
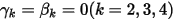получаем явную схему схема Эйлера в следующем виде:
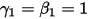и 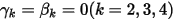получаем явную схему схема Эйлера в следующем виде: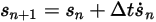
Уравнение 2.460
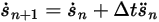
Уравнение 2.461
• Явный решатель Рунге - Кутты
Решатели Рунге - Кутты представляют собой явные схемы 2-го и 4-го порядка следующего вида:
◦ Схема второго порядка
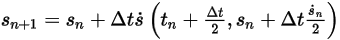
Уравнение 2.462
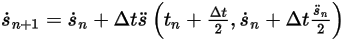
Уравнение 2.463
◦ Схема четвертого порядка
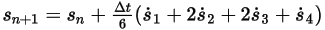
Уравнение 2.464
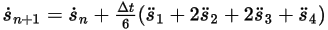
Уравнение 2.465
Здесь
Уравнение 2.466
Уравнение 2.467
Уравнение 2.468
Уравнение 2.469
• Решатель жестких систем (явный)
В дополнение к стандартным схемам Эйлера и Рунге - Кутты в Creo Flow Analysis был разработан решатель жестких систем, чтобы интегрировать ОДУ перемещения с одной степенью свободы. Это метод по умолчанию для динамического движения твердых тел.
Интегрирование уравнения вращения с одной степенью свободы
Как и для прямолинейного движения, подстановка уравнения 2.446 и уравнения 2.447 в уравнение 2.444 и явная группировка членов крутящих моментов с целью сокращения в один член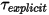 
позволяют переписать уравнение вращения с одной степенью свободы, уравнение 2.444, в следующей форме:
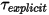позволяют переписать уравнение вращения с одной степенью свободы, уравнение 2.444, в следующей форме: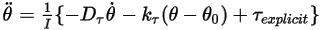
Уравнение 2.470
Здесь явно вычисляемый член крутящего момента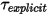 
имеет вид:
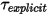имеет вид: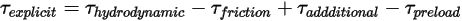
Уравнение 2.471
С заданными начальными и граничными условиями угол вращения получается интегрированием уравнения 2.470 с использованием явных схем шагов по времени. В зависимости от шага времени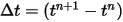 
общие формулы имеют следующий вид:
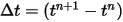общие формулы имеют следующий вид: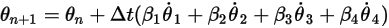
Уравнение 2.472
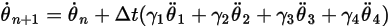
Уравнение 2.473
Здесь сумма весовых коэффициентов равна единице:
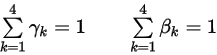
Уравнение 2.474
При выборе весовых коэффициентов легко выводятся различные числовые схемы. Еще раз приведем явные схемы Эйлера и Рунге - Кутты, как показано ниже:
• Явный решатель Эйлера (1-го порядка)
С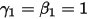 
и 
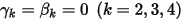получаем явную схему схема Эйлера в следующем виде:
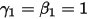и 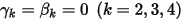получаем явную схему схема Эйлера в следующем виде: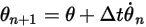
Уравнение 2.475
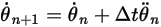
Уравнение 2.476
• Явный решатель Рунге - Кутты
Решатели Рунге - Кутты представляют собой явные схемы 2-го и 4-го порядка следующего вида:
◦ Схема второго порядка
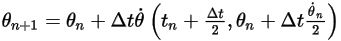
Уравнение 2.477
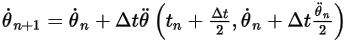
Уравнение 2.478
◦ Схема четвертого порядка
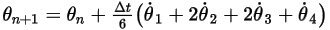
Уравнение 2.479
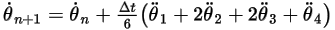
Уравнение 2.480
Здесь
Уравнение 2.481
Уравнение 2.482
Уравнение 2.483
Уравнение 2.484
• Решатель жестких систем (явный)
В дополнение к стандартным схемам Эйлера и Рунге - Кутты в Creo Flow Analysis был разработан решатель жестких систем, чтобы интегрировать ОДУ вращения с одной степенью свободы, уравнение 2.444. Это метод по умолчанию для динамического движения твердых тел.