Движения жесткого тела
В процессе моделирования поверхности твердотельного объекта обычно являются стеночными границами в области потока. Если на твердотельные объект или поверхность действуют динамические и механические силы, а также тепловые эффекты, некомпенсированная результирующая сила может вызывать движение и деформацию тела. Твердотельный объект в моделировании потоков часто рассматривается как жесткое тело. Таким образом, предполагается, что если на твердотельный объект действуют неуравновешенные силы, он может без деформации двигаться в линейном (перемещение) или угловом (вращение) направлениях либо одновременно перемещаться и вращаться. Однако для расчетной области CFA перемещение границ может привести к изменению области, а потому объемная сетка может деформироваться, как описано в модуле Поток (Flow).
Для жесткого тела уравнения, управляющие его движениями, выводятся непосредственно из сохранения линейного и углового импульса:
• Линейный импульс (перемещение)
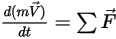
Уравнение 2.426
• Угловой импульс (вращение)
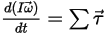
Уравнение 2.427
В уравнении 2.426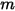
- масса перемещаемого объекта, 
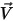-линейная/переносная скорость, а 
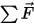- суммарная/результирующая сила, действующая на перемещаемое тело. В уравнении 2.427
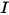- момент инерции, 
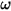⃗ - угловая скорость, а 
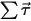⃗ - суммарный/результирующий крутящий момент, действующий на вращающееся тело.
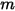- масса перемещаемого объекта, 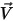-линейная/переносная скорость, а 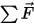- суммарная/результирующая сила, действующая на перемещаемое тело. В уравнении 2.427 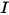- момент инерции, ⃗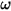 - угловая скорость, а ⃗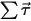 - суммарный/результирующий крутящий момент, действующий на вращающееся тело.Уравнение 2.426 и уравнение 2.427 описывают общее движение твердого тела с шестью степенями свободы, три степени свободы для перемещения и для вращения соответственно. Creo Flow Analysis в этом разделе рассматриваются только перемещение и вращение с одной степенью свободы.
Перемещение с одной степенью свободы
В предположении, что твердое тело движется линейно в произвольном направлении (остающимся неизменным), которое определено единичным вектором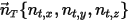 
, поступательное движение тела сводится к одной степени свободы. В результате для сохранения линейного импульса уравнение 2.426 становится скалярным уравнением вдоль направления движения, поскольку скорость движения и сила выражаются через 
:
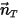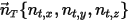, поступательное движение тела сводится к одной степени свободы. В результате для сохранения линейного импульса уравнение 2.426 становится скалярным уравнением вдоль направления движения, поскольку скорость движения и сила выражаются через :
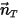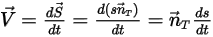
Уравнение 2.428
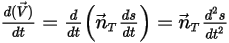
Уравнение 2.429
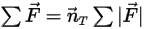
Уравнение 2.430
Здесь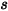 
- величина вектора позиции 
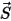в рассматриваемой точке твердого тела вдоль направления движения 
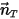. В декартовой системе координат получим следующее уравнение:
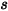- величина вектора позиции 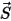в рассматриваемой точке твердого тела вдоль направления движения 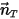. В декартовой системе координат получим следующее уравнение: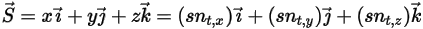
Уравнение 2.431
Если масса твердого тела остается постоянной, а элемент силы разложить так, чтобы явно включить все силы, действующие на тела, то для импульса получим следующее скалярное уравнение:
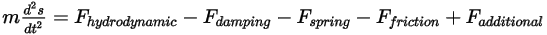
Уравнение 2.432
На правой стороне показаны следующие силы:
• Гидродинамическая сила 
- состоит из силы давления и силы сдвига. Они вызываются движением потока жидкости относительно поверхностей твердого тела, контактирующих с потоком. Силы давления и сдвига находятся из решений для потока (выходные величины):
- состоит из силы давления и силы сдвига. Они вызываются движением потока жидкости относительно поверхностей твердого тела, контактирующих с потоком. Силы давления и сдвига находятся из решений для потока (выходные величины):
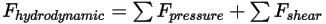
Уравнение 2.433
• Демпфирующая сила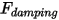 
- тормозящая сила, вызванная эффектом демпфирования трением. Она определяется движением твердотельного объекта и определенным пользователем коэффициентом демпфирования 
:
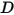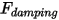- тормозящая сила, вызванная эффектом демпфирования трением. Она определяется движением твердотельного объекта и определенным пользователем коэффициентом демпфирования :
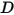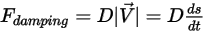
Уравнение 2.434
• Сила пружины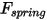 
- зависит от смещения пружины 
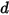, жесткости пружины 
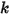и силы преднагружения пружины 
:
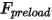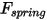- зависит от смещения пружины 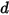, жесткости пружины 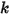и силы преднагружения пружины :
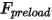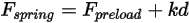
Уравнение 2.435
Здесь смещение пружины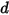 
определяется следующим образом:
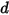определяется следующим образом: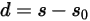
Уравнение 2.436
Здесь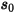 
- величина вектора позиции 
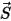в предыдущем расположении 
.
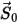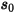- величина вектора позиции 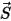в предыдущем расположении 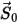.• Сила трения - для учета воздействия трения в динамической системе принята контактная модель трения. Сила трения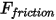 
моделируется как:
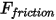моделируется как: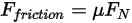
Уравнение 2.437
Здесь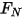 
- нормальный компонент контактной силы, действующей на поверхность твердого тела. Для коэффициента трения 
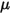коэффициент трения покоя 
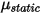и коэффициент трения скольжения 
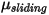вводятся в дальнейшем для стационарных и движущих тел соответственно:
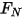- нормальный компонент контактной силы, действующей на поверхность твердого тела. Для коэффициента трения 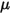коэффициент трения покоя 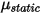и коэффициент трения скольжения 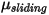вводятся в дальнейшем для стационарных и движущих тел соответственно: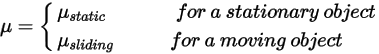
Уравнение 2.438
• Дополнительная сила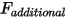 
- добавляется для дополнительных определяемых пользователем сил.
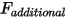- добавляется для дополнительных определяемых пользователем сил.Вращение с одной степенью свободы
Если произвольная ось вращения определена точкой (центром оси)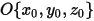 
и единичным вектором направления 
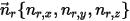, вращение твердого тела вокруг оси 
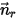также сводится к вращению с одной степенью свободы. Аналогично для углового импульса уравнение 2.427 также превращается в скалярное уравнение в касательном направлении 
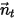, которое определяется как:
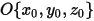и единичным вектором направления 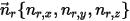, вращение твердого тела вокруг оси 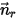также сводится к вращению с одной степенью свободы. Аналогично для углового импульса уравнение 2.427 также превращается в скалярное уравнение в касательном направлении 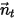, которое определяется как: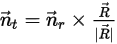
Уравнение 2.439
Здесь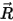 
- вектор, указывающий от центра оси к произвольной точке 
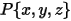твердого тела.
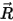- вектор, указывающий от центра оси к произвольной точке 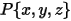твердого тела.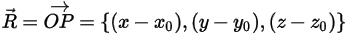
Уравнение 2.440
Угловая скорость и крутящий момент в точке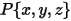 
переписываются следующим образом:
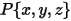переписываются следующим образом: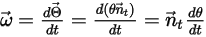
Уравнение 2.441
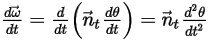
Уравнение 2.442
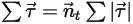
Уравнение 2.443
Здесь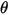 
- угол поворота точки
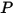относительно начального или опорного расположения.
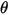- угол поворота точки 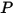относительно начального или опорного расположения.Если момент инерции остается постоянным, а элемент крутящего момента развертывается для явного включения всех крутящих моментов, приложенных к вращающемуся телу, мы имеем скалярное уравнение для углового импульса:
Уравнение 2.444
Члены крутящего момента на правой стороне определяются следующим образом:
• Гидродинамический крутящий момент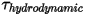 
- комбинация крутящего момента сил давления и сдвига:
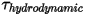- комбинация крутящего момента сил давления и сдвига: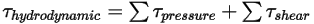
Уравнение 2.445
• Демпфирующий крутящий момент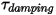 
- зависит от скорости вращения 
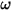и определяемого пользователем коэффициента демпфирования 
:
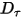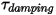- зависит от скорости вращения 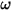и определяемого пользователем коэффициента демпфирования :
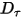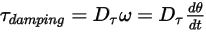
Уравнение 2.446
• Крутящий момент пружины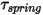 
- крутящий момент, инициированный кручением, который зависит от угла смещения 
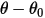, определяемого пользователем крутящего момента преднагружения 
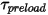и постоянной кручения 
.
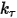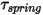- крутящий момент, инициированный кручением, который зависит от угла смещения 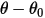, определяемого пользователем крутящего момента преднагружения 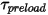и постоянной кручения .
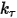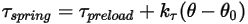
Уравнение 2.447
Здесь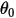 
- опорный угол. Обычно это положение границы или объема во время настройки модели, но может соответствовать другому расположению. Например, при нулевом угловом смещении опорный угол 
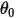не совпадает с начальным угловым положением.
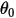- опорный угол. Обычно это положение границы или объема во время настройки модели, но может соответствовать другому расположению. Например, при нулевом угловом смещении опорный угол 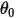не совпадает с начальным угловым положением.• Крутящий момент трения - крутящий момент, вызванный силой трения, возникающей при перемещении двух контактирующих объектов. В экспериментах он определяется разностью приложенного крутящего момента и наблюдаемого или полного крутящего момента. Он зависит от коэффициента трения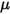 
и крутящего момента контакта по причине перпендикулярной силы 
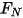, приложенной к поверхности контакта:
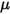и крутящего момента контакта по причине перпендикулярной силы 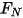, приложенной к поверхности контакта: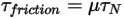
Уравнение 2.448
Здесь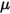 
- определяемый пользователем параметр, определенный в уравнении 2.438.
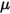- определяемый пользователем параметр, определенный в уравнении 2.438.• Дополнительные моменты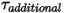 
- добавлены для дополнительных определяемых пользователем крутящих моментов.
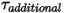- добавлены для дополнительных определяемых пользователем крутящих моментов.Модель отражения
Во многих ситуациях твердое тело только перемещается или вращается либо одновременно перемещается и вращается в ограниченном пространстве (на ограниченное расстояние или угол), т. е. может иметь максимальную и/или минимальную позиции. Например, как показано на следующем рисунке, при освобождении простого гравиметрического маятника из исходного положения с углом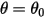 
восстанавливающая сила, действующая на его массу, приводит к колебаниям относительно положения равновесия. Максимальный угол с любой стороны от положения равновесия 
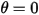зависит от позиции отпускания 
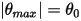. Если нет трения (подвеска без трения в вакууме), максимальный угол остается постоянным и маятник качается взад-вперед с одинаковыми крайними положениями. Однако если маятник находится, например, в атмосфере, сопротивление воздуха (демпфирование) приводит к тому, что максимальный угол раскачивания уменьшается со временем и маятник в конце концов останавливается в положении равновесия.
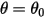восстанавливающая сила, действующая на его массу, приводит к колебаниям относительно положения равновесия. Максимальный угол с любой стороны от положения равновесия 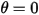зависит от позиции отпускания 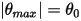. Если нет трения (подвеска без трения в вакууме), максимальный угол остается постоянным и маятник качается взад-вперед с одинаковыми крайними положениями. Однако если маятник находится, например, в атмосфере, сопротивление воздуха (демпфирование) приводит к тому, что максимальный угол раскачивания уменьшается со временем и маятник в конце концов останавливается в положении равновесия.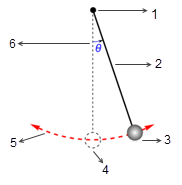
рис.
1. Точка поворота без трения
2. Безмассовый стержень
3. Массивный маятник
4. Положение равновесия
5. Траектория маятника
6. Амплитуда
Кроме того, в цикле качания (периодическом), когда маятник приходит в самое высокое положение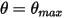 
, меняется направление его движения с полной потерей кинетической энергии. В простом гравиметрическом маятнике кинетическая энергия полностью переходит в потенциальную энергию, тогда как при учете сопротивления среды часть кинетической энергии теряется на преодоление вязкостного сопротивления. Однако результирующая сила или потенциальная энергия заставляют маятник двигаться в противоположном направлении к точке равновесия, где кинетическая энергия (скорость) является максимальной, а потенциальная энергия - самой низкой. В этом случае 
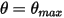указывает на отсутствие отражения в уравнении 2.444 для углового импульса с одной степенью свободы.
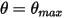, меняется направление его движения с полной потерей кинетической энергии. В простом гравиметрическом маятнике кинетическая энергия полностью переходит в потенциальную энергию, тогда как при учете сопротивления среды часть кинетической энергии теряется на преодоление вязкостного сопротивления. Однако результирующая сила или потенциальная энергия заставляют маятник двигаться в противоположном направлении к точке равновесия, где кинетическая энергия (скорость) является максимальной, а потенциальная энергия - самой низкой. В этом случае 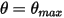указывает на отсутствие отражения в уравнении 2.444 для углового импульса с одной степенью свободы.В дополнение к условию отсутствия отражения движущееся тело в ограничивающей позиции может не терять всю кинетическую энергию и отражаться назад (полное отражение) или терять только часть кинетической энергии (частичное отражение). Таким образом, применяются следующие три условия отражения, когда динамические уравнения перемещения и вращения с одной степенью свободы, уравнение 2.432 и уравнение 2.444 решаются, чтобы определить движение твердого тела или стеночной границы для области потока:
• Без отражения - модель в Creo Flow Analysis по умолчанию. Определяет, что когда достигается предел движения твердого тела или границы, направление движения изменяется с полной потерей кинетической энергии. Когда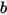 
и 
представляют отражение и падение, а 
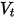и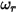 
- скорости перемещения и вращения (только величины), эта модель отражения выражается следующим образом:
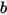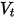и представляют отражение и падение, а и 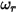- скорости перемещения и вращения (только величины), эта модель отражения выражается следующим образом:◦ Перемещение
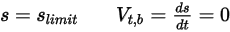
Уравнение 2.449
◦ Вращение
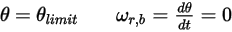
Уравнение 2.450
• Частичное отражение - модель, которая определяет, что когда достигается предел движения твердого тела или границы, направление движения изменяется с частичной потерей кинетической энергии, определяемой указанным пользователем фактором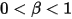 
:
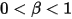:◦ Перемещение
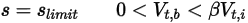
Уравнение 2.451
◦ Вращение
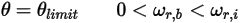
Уравнение 2.452
• Упругое отражение - модель, которая определяет, что при достижении предела движения твердого тела или границы направление движения изменяется без потери кинетической энергии,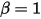 
:
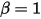:◦ Перемещение
Уравнение 2.453
◦ Вращение
Уравнение 2.454