열 방사 특성
열 방사의 특성은 내보내는 객체 또는 바디의 다음 특성에 따라 달라집니다.
• 서피스 온도
• 서피스 부드러움 또는 미세도
• 스펙트럼 흡수율
• 스펙트럼 발광력
전자기 파형인 열 방사는 주파수 또는 파장 스펙트럼을 가진 광자 에너지의 연속 분산으로 구성됩니다. 발광 바디의 경우 스펙트럼 분포, 파장의 피크 값 및 모든 파장의 총 방사량은 발광 바디의 서피스 온도에 따라 달라집니다. 반대로, 주어진 서피스 온도에서 발광 바디의 흡수율, 반사율 및 방사율은 모두 방사의 파장에 의존합니다.
방사 에너지 교환
모든 바디는 임의 단계와 주파수로 임의의 방향으로 이동하는 광자 형태의 에너지를 방사합니다. 방사된 광자가 한 바디의 서피스에서 다른 바디의 서피스에 도달하는 경우 그림 2.35와 같이 해당 바디를 흡수, 반사 및/또는 전송할 수 있습니다. 이에 대한 방사 문제가 있는 서피스의 동작은 다음 수량으로 설명할 수 있습니다.
참고 문헌: R. Siegel and J. R. Howell, "Thermal Radiation Heat Transfer", Hemisphere Publishing Corporation, Washington DC, 1992.
• 흡수율 α - 주어진 파장에서 흡수된 입사 방사의 비율입니다.
• 반사율 ρ - 주어진 파장에서 반사된 입사 방사의 비율입니다.
• 전송율 τ - 주어진 파장에서 전송된 입사 방사의 비율입니다.
세 개의 계수는 방사 λ에서 전자파의 파장 함수입니다. 에너지 고려 사항에서는 모두 합하여 통합해야 합니다.
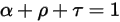
방정식 2.273
Kirchhoff의 열 방사 법칙에 따라 방출 바디의 방사율은 상호 의존으로 인해 특정 파장에 대한 스펙트럼 흡수율과 같습니다.
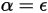
방정식 2.274
여기서 ε는 방사율이고, 방출 바디에서 동일한 온도 및 파장 아래의 완전한 방사체(검정색 바디)를 기준으로 하는 방출 에너지 비율입니다.
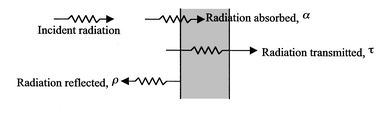
그림 2.35
방정식 2.273은 열 방사와 관련된 바디 반응의 동작이 흡수율 α, 반사율 ρ 및 전송률 τ에 의해 규정되는 방식을 나타냅니다. α, ρ, τ의 값에 따라 다음과 같이 이상적인 발광 바디 유형이 정의됩니다.
R. Siegel and J. R. Howell, "Thermal Radiation Heat Transfer", Hemisphere Publishing Corporation, Washington DC, 1992
• 불투명 바디 - 방사를 전송하지 않지만 일부 방사를 반사할 수 있습니다. τ=0 및 α+ρ=1
• 투명 바디 - 모든 방사를 전송합니다. τ=1 및 α=ρ=0
• 검정색 바디 - 플랑크가 제안한 이론적 모델입니다. 검정색 바디는 주파수 또는 발생 각도에 상관없이 모든 파장의 모든 입사 전자기 방사를 흡수하는 객체입니다. 전자파 방출 객체가 열역학적 평형의 검정색 바디에 대한 물리적 특성을 충족하는 경우, 이 방사를 검정색 바디 방사라고 합니다. 검정색 바디의 경우 α=ε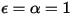 및
및 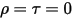 입니다.
입니다.
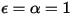 및
및 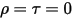 입니다.
입니다.• 흰색 바디 - 모든 입사 광선을 모든 방향으로 완전히 균일하게 반사한다고 가정합니다. 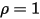 및
및 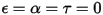
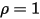 및
및 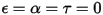
• 회색 바디 - 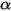 및
및 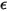 가 온도 및 파장에 독립적인 바디입니다.
가 온도 및 파장에 독립적인 바디입니다.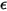 는 모든 파장에 대해 균일합니다. 회색 바디 또는 서피스의 방사를 회색 방사라고 합니다. 회색 방사와 달리, 파장 스펙트럼을 가진 열 방사를 비 회색 방사라고 합니다.
는 모든 파장에 대해 균일합니다. 회색 바디 또는 서피스의 방사를 회색 방사라고 합니다. 회색 방사와 달리, 파장 스펙트럼을 가진 열 방사를 비 회색 방사라고 합니다.
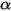 및
및 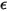 가 온도 및 파장에 독립적인 바디입니다.
가 온도 및 파장에 독립적인 바디입니다.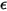 는 모든 파장에 대해 균일합니다. 회색 바디 또는 서피스의 방사를 회색 방사라고 합니다. 회색 방사와 달리, 파장 스펙트럼을 가진 열 방사를 비 회색 방사라고 합니다.
는 모든 파장에 대해 균일합니다. 회색 바디 또는 서피스의 방사를 회색 방사라고 합니다. 회색 방사와 달리, 파장 스펙트럼을 가진 열 방사를 비 회색 방사라고 합니다.방사 전력
• 전력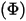 - 주어진 소스에 대해 단위 시간당 방사, 반사, 전송 또는 수신된 총 또는 순 방사 에너지입니다.
- 주어진 소스에 대해 단위 시간당 방사, 반사, 전송 또는 수신된 총 또는 순 방사 에너지입니다.
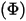 - 주어진 소스에 대해 단위 시간당 방사, 반사, 전송 또는 수신된 총 또는 순 방사 에너지입니다.
- 주어진 소스에 대해 단위 시간당 방사, 반사, 전송 또는 수신된 총 또는 순 방사 에너지입니다.• 복사조도(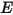 ) - 단위 면적당 서피스
) - 단위 면적당 서피스 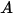 를 통해 받은 방사 전력입니다.
를 통해 받은 방사 전력입니다. 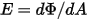
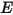 ) - 단위 면적당 서피스
) - 단위 면적당 서피스 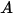 를 통해 받은 방사 전력입니다.
를 통해 받은 방사 전력입니다. 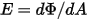
• 방사력(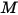 ) - 단위 면적당 서피스
) - 단위 면적당 서피스 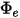 를 통해 받은 방사 전력입니다.
를 통해 받은 방사 전력입니다. 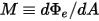
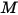 ) - 단위 면적당 서피스
) - 단위 면적당 서피스 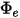 를 통해 받은 방사 전력입니다.
를 통해 받은 방사 전력입니다. 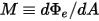
• 강도(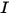 ) - 주어진 소스에 대해 주어진 방향(솔리드 각도
) - 주어진 소스에 대해 주어진 방향(솔리드 각도 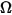 )으로 방사되는 전력입니다.
)으로 방사되는 전력입니다. 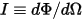
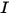 ) - 주어진 소스에 대해 주어진 방향(솔리드 각도
) - 주어진 소스에 대해 주어진 방향(솔리드 각도 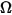 )으로 방사되는 전력입니다.
)으로 방사되는 전력입니다. 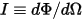
• 복사휘도(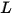 ) - 단위 투영된 면적당 단위 솔리드 각도당 주어진 서피스에 의해 방사, 반사, 전송 또는 수신된 방사 전력입니다.
) - 단위 투영된 면적당 단위 솔리드 각도당 주어진 서피스에 의해 방사, 반사, 전송 또는 수신된 방사 전력입니다. 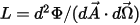
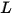 ) - 단위 투영된 면적당 단위 솔리드 각도당 주어진 서피스에 의해 방사, 반사, 전송 또는 수신된 방사 전력입니다.
) - 단위 투영된 면적당 단위 솔리드 각도당 주어진 서피스에 의해 방사, 반사, 전송 또는 수신된 방사 전력입니다. 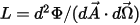
• 플랑크 법칙
임의의 온도에서 바디에 의해 방사된 열 방사는 광범위한 주파수로 구성됩니다. 검정 바디의 경우 객체의 온도에만 해당하는 검정 바디 방사의 도수 분포를 플랑크 법칙으로 설명합니다. 플랑크는 검정 바디의 스펙트럼 복사휘도 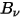 가 단위 면적당, 방사가 측정된 단위 솔리드 각도당, 단위 주파수당
가 단위 면적당, 방사가 측정된 단위 솔리드 각도당, 단위 주파수당 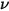 방사된 전력으로 정의되며, 바디 온도에 대한 공식이 있음을 보여줍니다.
방사된 전력으로 정의되며, 바디 온도에 대한 공식이 있음을 보여줍니다.
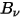 가 단위 면적당, 방사가 측정된 단위 솔리드 각도당, 단위 주파수당
가 단위 면적당, 방사가 측정된 단위 솔리드 각도당, 단위 주파수당 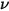 방사된 전력으로 정의되며, 바디 온도에 대한 공식이 있음을 보여줍니다.
방사된 전력으로 정의되며, 바디 온도에 대한 공식이 있음을 보여줍니다.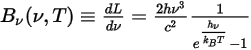
방정식 2.275
여기서 각 항목은 다음을 나타냅니다.
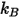 | 볼츠만 상수 |
h | 플랑크 상수 |
c | 진공 또는 재료 매체의 광속 |
스펙트럼 복사휘도는 단위 파장 λ당으로도 표현됩니다.
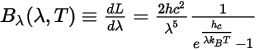
방정식2.276
• 슈테판 볼츠만 법칙:
주파수 v에 대한 플랑크 법칙의 통합을 통해, 슈테판 볼츠만 법칙에 따라 주어진 전력 출력은 온도에 따라 검정색 바디에서 방사되는 전력입니다. 슈테판 볼츠만 법칙은 검정색 바디 방사 방출이라고도 합니다. 슈테판 볼츠만 법칙에 따르면, 단위 시간당 모든 파장에서 검정색 바디의 단위 표면적당 방사되는 총 에너지는 검정색 바디의 열역학 온도의 네 번째 전력에 직접 비례합니다(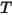 ).
).
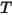 ).
).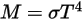
2.277
여기서 각 항목은 다음을 나타냅니다.
σ | 슈테판 볼츠만 상수 |
M | 방사 방출 |
모든 입사 방사를 흡수하지 않는 회색 바디의 경우에는 검정색 바디보다 더 적은 총 에너지를 방사합니다. 방사율 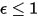 (검정색 바디:
(검정색 바디: 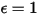 )이 도입됨에 따라 방정식 2.277이 회색 바디로 확장됩니다.
)이 도입됨에 따라 방정식 2.277이 회색 바디로 확장됩니다.
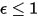 (검정색 바디:
(검정색 바디: 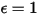 )이 도입됨에 따라 방정식 2.277이 회색 바디로 확장됩니다.
)이 도입됨에 따라 방정식 2.277이 회색 바디로 확장됩니다.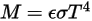
2.278
슈테판 볼츠만 법칙에 따르면 바디에 의해 방사되는 복사휘도 및 전력은 다음과 같이 계산됩니다.
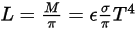
방정식 2.279
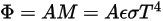
방정식 2.280
• 빈의 변위 법칙
빈의 변위 법칙에 따르면, 단위 파장당 검정색 바디 복사의 스펙트럼 복사휘도가 최대값에 도달하는 파장 λ는 온도에 반비례합니다.
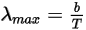
방정식 2.281
여기서 b는 빈의 변위 상수입니다.
모델 상수
다음 표는 위의 이론적 모델에 사용되는 모델 상수입니다.
h | 플랑크 상수 | 6.626 069 3(11) ×10-34J-s = 4.135 667 43(35) ×10-15eV-s |
b | 빈의 변위 상수 | 2.897 768 5(51) ×10-3m-K |
kB | 볼츠만 상수 | 1.380 650 5(24) ×10-23J/K = 8.617 343 (15) ×10-5eV/K |
σ | 슈테판 볼츠만 상수 | 5.670 373 (21) ×10-8 W/(m2-K4) |
c | 광속 | 299 792 458m/s |