Problem der dynamischen Frequenzanalyse
Dieses Kapitel enthält ein Problem der dynamischen Frequenzanalyse und die Ergebnisse von Structure. In einer dynamischen Frequenzanalyse berechnet Structure die Amplitude und Phase von Verschiebungen, Geschwindigkeiten, Beschleunigungen und Spannungen in Ihrem Modell, die als Antwort auf eine oszillierende Last mit unterschiedlichen Frequenzen auftreten. Structure berechnet zudem automatisch alle vordefinierten Messgrößen. Diese Liste der Messgrößen variiert je nach dem Analysetyp.
mvsf001: Harmonische Reaktion eines Federsystems mit zwei Massen
|
Analysetyp:
|
Dynamische Frequenzanalyse
|
|
Modelltyp:
|
3D
|
|
Vergleich:
|
ANSYS No. 90
|
|
Hintergrundinformation:
|
Thomson, W. T. Vibration Theory and Applications. Prentice-Hall, Inc., Englewood Cliffs, N. J., 2. Ausgabe, 1965.
|
|
Beschreibung:
|
Ermitteln Sie die Reaktion eines Federsystems mit zwei Massen, das von einer harmonischen Kraft angeregt wird, die auf die Masse an Punkt B einwirkt.
|

Spezifikationen
Art des Elements: | Masse (2), Feder (3) | ||
Einheiten: | IPS | ||
Bemaßungen: | Federlänge: 1 (beliebig) | ||
Masseneigenschaften: | |||
M: 0.5 | Mxx: 0 | Mxy: 0 | Mxz: 0 |
Myy: 0 | Myz: 0 | Mzz: 0 | |
Federeigenschaften: (Dehnsteifigkeit) | |||
Kxx: 200 | Kxy: 0 | Kxz: 0 | |
Kyy: 0 | Kyz: 0 | Kzz: 0 | |
Randbedingungen: | Position: | Freiheitsgrade: |
|---|---|---|
constraint1 | platziert auf den Punkten A und D platziert auf den Punkten B und C | konstant in allen FG konstant in allen FG außer VerschX |
Lasten: | Ort/Betrag: | Verteilung: | Räumliche Verteilung: |
|---|---|---|---|
load1 | platziert auf Punkt B: FX = 200 | Nicht zutreffend | Nicht zutreffend |
Vergleich der Ergebnisdaten
Pos. | Theorie | ANSYS | Struktur1 | % Diff. | |
|---|---|---|---|---|---|
Frequenz = 1.5 Hz Verschiebung/Phase bei B, C (m=dispx_2, 3/ phase_2, 3) | Punkt B | 0.8227/0 | 0.8227/0 | 0.8227/0 | 0 % |
Punkt C | 0.4627/0 | 0.4627/0 | 0.4627/0 | 0 % | |
Frequenz = 4.0 Hz Verschiebung/Phase bei A, B (m=dispx_2, 3/ phase_2, 3) | Punkt B | 0.5115/ 180 | 0.5115/ 180 | 0.5115/180 | 0 % |
Punkt C | 1.2153/ 180 | 1.2153/ 180 | 1.215/180 | 0 % | |
Frequenz = 6.5 Hz Verschiebung/Phase bei A, B (m=dispx_2, 3/ phase_2, 3) | Punkt B | 0.5851/ 180 | 0.5851/ 180 | 0.5851/180 | 0 % |
Punkt C | 0.2697/0 | 0.2697/0 | 0.2697/0 | 0 % | |
Konvergenz %: 0 % Frequenz und Lokale Versch. | Max P: 1 | Anz. Gleichungen: 2 | |||
1 Sie können die Ergebnisse im Statusbericht nicht anzeigen. Definieren Sie stattdessen ein Messergebnisfenster, und lassen Sie sich den Graphen anzeigen.
mvsf002: harmonische Schwingungsreaktion für tiefen gelenkig gelagerten Balken
Analysetyp: | Dynamische Frequenzanalyse |
Modelltyp: | Balken (Beam) |
Vergleich: | NAFEMS-Benchmark |
Hintergrundinformation: | Ausgewählte Benchmarks für erzwungene Vibration, Bericht Nr. E1261/R002 Ausgabe 03.2/9 Februar 1989, S. 17. Test 5H |
Beschreibung: | Bestimmen Sie die Reaktion eines gelenkig gelagerten quadratischen Balkens, der von einer harmonischen Kraft angeregt wird, die einheitlich über den Balken verteilt ist. |

Spezifikationen
Art des Elements: | Quadratischer Balken | |
Einheiten: | MKS | |
Bemaßungen: | L: 10.0, a =2 | |
Materialeigenschaften: | Massendichte: 8000 Elastizitätsmodul: 2e11 | Querkontraktionszahl: 0.3 |
Randbedingungen: | Position: | Freiheitsgrade: |
|---|---|---|
Platziert auf Punkt A Platziert auf Punkt B: | Konstant in VerschX, VerschY, VerschZ und Rotation Rx Konstant in VerschY und VerschZ |
Lasten | Details |
|---|---|
Kraft Fy = 1e6 N/m, Dämpfung = 2 % in allen 16 Modi verwendet, Frequenzbereich 0 bis 60 Hz |
Vergleich der Ergebnisdaten
NAFEMS | Struktur | % Diff. | |
|---|---|---|---|
Spitzenverschiebung in der Mitte (mm) | 13.45 | 13.5129 | 0.467 |
Frequenz (Hz) | 42.65 | 42.6002 | 0.116 |
mvsf003: harmonische Schwingungsreaktion für tiefes gelenkig gelagertes dünnes Quadrat
Analysetyp: | Dynamische Frequenzanalyse |
Modelltyp: | 3D |
Vergleich: | NAFEMS-Benchmark |
Hintergrundinformation: | Ausgewählte Benchmarks für erzwungene Vibration, Bericht Nr. E1261/R002 Ausgabe 03./9. Februar 1989 S. 23. Test 13H |
Beschreibung: | Bestimmen Sie die Reaktion einer gelenkig gelagerten dünnen quadratischen Platte, die von einer harmonischen Kraft angeregt wird, die einheitlich über die Platte verteilt ist. |
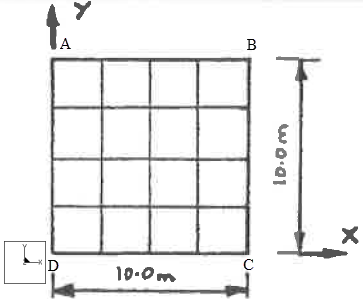
Spezifikationen
Art des Elements: | Schale | |
Einheiten: | MKS | |
Bemaßungen: | L: 10.0, Dicke: 0.05 | |
Materialeigenschaften: | Massendichte: 8000 Elastizitätsmodul: 2e11 | Querkontraktionszahl: 0.3 |
Randbedingungen: | Position: | Freiheitsgrade: |
|---|---|---|
Platziert auf Kanten AD und BC: Platziert auf Kanten AB und DC: | Konstant in VerschY, VerschZ, RotX und RotZ Konstant in VerschX, VerschZ, RotY und RotZ |
Lasten | Details |
|---|---|
Kraft Fy = 100 Pa, Dämpfung = 2 % in allen 16 Modi verwendet, Frequenzbereich 0 bis 4.16 Hz |
Vergleich der Ergebnisdaten
NAFEMS | Struktur | % Diff. | |
|---|---|---|---|
Spitzenverschiebung in der Mitte der Platte (mm) | 45.42 | 45.4466 | 0.0585 |
Frequenz (Hz) | 2.377 | 2.37603 | 0.0408 |