Probleme der Modalanalyse
Dieses Kapitel enthält Probleme von Modalanalysen und die Ergebnisse von Creo Simulate. Bei einer Modalanalyse berechnet Structure die Eigenschwingungen und Eigenmodenformen eines Modells. Structure berechnet zudem automatisch alle vordefinierten Messgrößen. Diese Liste der Messgrößen variiert je nach dem Analysetyp.
Dieses Kapitel enthält die folgenden Probleme:
mvsm001: 2D Ebener Dehnungszustand Schale Auslegerplatte
|
Analysetyp:
|
Modalanalyse
|
|
Modelltyp:
|
2D Ebener Dehnungszustand
|
|
Vergleich:
|
Theoretische Ergebnisse
|
|
Hintergrundinformation:
|
Roark, R.J. und Young, W.C. Formulas for Stress and Strain. NY: McGraw-Hill Book Co. 1982. S. 576-578.
|
|
Beschreibung:
|
Ermitteln Sie die Grundfrequenz einer Auslegerplatte in einem Modell mit planarem Dehnungszustand.
|
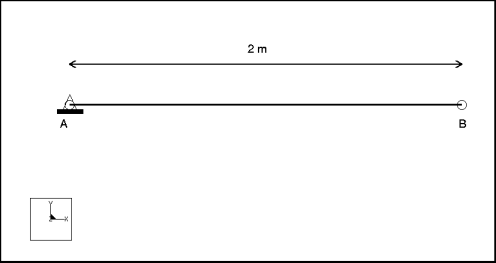
Spezifikationen
Art des Elements: | 2D-Schalenelement (1) | |
Einheiten: | MKS | |
Bemaßungen: | Breite: 2 Dicke: 0.01 | |
Materialeigenschaften: | Massendichte: 7850 Massenspezifische Materialkosten: 0 Elastizitätsmodul: 2e11 | Querkontraktionszahl: 0.3 Wärmeausdehnung: 0 Leitfähigkeit: 0 |
Randbedingung: | platziert auf Punkt A: konstant in allen FG | |
Vergleich der Ergebnisdaten
Theorie | Struktur | % Differenz | |
|---|---|---|---|
Grundfrequenz (Hz) (mode=1) | 2.1393 | 2.1374 | 0.08 % |
Konvergenz %: 0.4 % Frequenz | Max P: 4 | Anz. Gleichungen: 12 | |
mvsm002: 2D Ebener Spannungszustand Auslegerplatte
Analysetyp: | Modalanalyse |
Modelltyp: | 2D Ebener Spannungszustand |
Vergleich: | Theoretische Ergebnisse |
Hintergrundinformation: | Roark, R.J. und Young, W.C. Formulas for Stress and Strain. NY: McGraw-Hill Book Co. 1982. S. 576-578. |
Beschreibung: | Ermitteln Sie die Grundfrequenz der Seitenschwingung einer Auslegerplatte. |

Spezifikationen
Art des Elements: | 2D-Plattenelement (1) | |
Einheiten: | IPS | |
Bemaßungen: | Länge: 36 Breite: 4 Dicke: 0.1 | |
Materialeigenschaften: | Massendichte: 7.28e4 Massenspezifische Materialkosten: 0 Elastizitätsmodul: 3e7 | Querkontraktionszahl: 0.3 Wärmeausdehnung: 0 Leitfähigkeit: 0 |
Randbedingung: | platziert auf Kante A-B: konstant in VerschX und VerschY | |
Vergleich der Ergebnisdaten
Theorie | Struktur | % Differenz | |
|---|---|---|---|
Grundfrequenz (Hz) (mode=1) | 101.326 | 100.988 | 0.33 % |
Konvergenz %: 0.4 % Frequenz | Max P: 6 | Anz. Gleichungen: 42 | |
mvsm003: 2D Ebener Dehnungszustand Volumenkörper Auslegerplatte
Analysetyp: | Modalanalyse |
Modelltyp: | 2D Ebener Dehnungszustand |
Vergleich: | Theoretische Ergebnisse |
Hintergrundinformation: | Roark, R.J. und Young, W.C. Formulas for Stress and Strain, NY: McGraw-Hill Book Co. 1982. S. 576-578. |
Beschreibung: | Ermitteln Sie die Grundfrequenz einer Auslegerplatte in einem Modell mit planarem Dehnungszustand. |
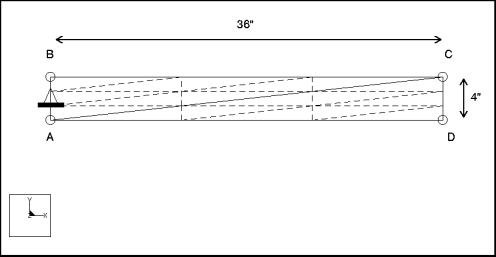
Spezifikationen
Art des Elements: | 2D-Volumenkörper (2) | |
Einheiten: | IPS | |
Bemaßungen: | Länge: 36 Breite: 4 | |
Materialeigenschaften: | Massendichte: 7.28e4 Massenspezifische Materialkosten: 0 Elastizitätsmodul: 3e7 | Querkontraktionszahl: 0.3 Wärmeausdehnung: 0 Leitfähigkeit: 0 |
Randbedingung: | platziert auf Kante A-B: konstant in VerschX, VerschY und RotZ | |
Vergleich der Ergebnisdaten
Theorie | Struktur | % Differenz | |
|---|---|---|---|
Grundfrequenz (Hz) (mode=1) | 106.219 | 106.604 | 0.36% |
Konvergenz %: 0.8 % Frequenz | Max P: 6 | Anz. Gleichungen: 42 | |
mvsm004: 2D Achsensymmetrische Radialschwingung eines Kreisrings
Analysetyp: | Modalanalyse |
Modelltyp: | 2D-Achsensymmetrie |
Vergleich: | ANSYS No. 67 |
Hintergrundinformation: | Timoshenko, S., und Young, D.H. Vibration Problems in Engineering. 3. Ausgabe D. Van Nostrand Co., Inc. 1955. Seite 425, Art. 68. |
Beschreibung: | Ermitteln Sie die Grundfrequenz der Radialschwingung eines Kreisrings in einem achsensymmetrischen Modell. |
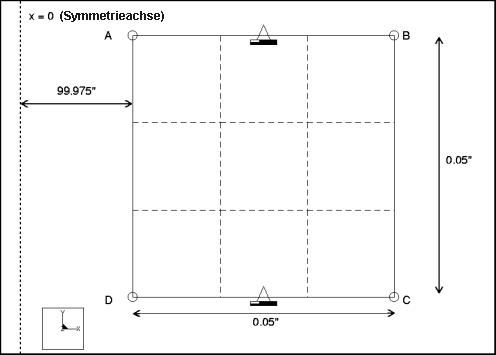
Spezifikationen
Art des Elements: | 2D-Volumenkörper (1) | |
Einheiten: | IPS | |
Bemaßungen: | Innenradius: 99.975 Außenradius: 100.025 Höhe: 0.05 | |
Materialeigenschaften: | Masse-Dichte: 7.3e4 Massenspezifische Materialkosten: 0 Elastizitätsmodul: 3e7 | Querkontraktionszahl: 0 Wärmeausdehnung: 0 Leitfähigkeit: 0 |
Randbedingungen: | platziert auf Kante A-B: konstant in VerschY und RotZ platziert auf Kante C-D: konstant in VerschY und RotZ | |
Vergleich der Ergebnisdaten
Theorie | ANSYS | Struktur | % Differenz | |
|---|---|---|---|---|
Radialfrequenz (Hz) (mode=1) | 322.64 | 322.64 | 322.64 | 0.0 % |
Konvergenz %: 0.0 % Frequenz | Max P: 2 | Anz. Gleichungen: 10 | ||
mvsm005: 3D Radialschwingung eines Rings
Analysetyp: | Modalanalyse |
Modelltyp: | 3D |
Vergleich: | Theoretische Ergebnisse |
Hintergrundinformation: | Love, A.E.H. A Treatise on the Mathematical Theory of Elasticity. 4. Ausgabe NY: Dover Publications. 1944. S. 452, Art. 293b. |
Beschreibung: | Ermitteln Sie die erste und zweite Eigenfrequenz der Radialschwingung eines Rings in einem Viertelmodell. |

Spezifikationen
Art des Elements: | Balken (1) | |
Einheiten: | IPS | |
Bemaßungen: | Radius: 2 | |
Balkeneigenschaften: | Bereich: 0.01 IYY: 1e3 Schub FY: 0.83333 CY: 1 | J: 1.008e3 IZZ: 8.33e6 Schub FZ: 0.83333 CZ: 1 |
Materialeigenschaften: | Massendichte: 7.28e4 Massenspezifische Materialkosten: 0 Elastizitätsmodul: 3e7 | Querkontraktionszahl: 0.3 Wärmeausdehnung: 0 Leitfähigkeit: 0 |
Randbedingungen: | platziert auf Punkt A: konstant in allen FG außer VerschX platziert auf Punkt B: konstant in allen FG außer VerschY | |
Vergleich der Ergebnisdaten
Theorie | Struktur | % Differenz | |
|---|---|---|---|
Eigenfrequenz 1 (Hz) | 625.65 | 624.43 | 0.19 % |
Eigenfrequenz 2 (Hz) | 3393.06 | 3369.13 | 0.70 % |
Konvergenz %: 0.0 % Frequenz | Max P: 9 | Anz. Gleichungen: 50 | |
mvsm006: 3D Keilförmige Auslegerplatte
Analysetyp: | Modalanalyse |
Modelltyp: | 3D |
Vergleich: | ANSYS No. 62 |
Hintergrundinformation: | Timoshenko, S., und Young, D.H. Vibration Problems in Engineering. 3. Ausgabe D. Van Nostrand Co., Inc. 1955. Seite 392, Art 62. |
Beschreibung: | Ermitteln Sie die Grundfrequenz der Seitenschwingung einer keilförmigen Auslegerplatte. |

Spezifikationen
Art des Elements: | Schalenelement (1) | |
Einheiten: | IPS | |
Bemaßungen: | Länge: 16 Breite: 4 Dicke: 1 | |
Materialeigenschaften: | Massendichte: 7.28e4 Massenspezifische Materialkosten: 0 Elastizitätsmodul: 3e7 | Querkontraktionszahl: 0 Wärmeausdehnung: 0 Leitfähigkeit: 0 |
Randbedingung: | platziert auf Kante A-B: konstant in allen FG | |
Vergleich der Ergebnisdaten
Theorie | ANSYS | Struktur | % Differenz | |
|---|---|---|---|---|
Frequenz (Hz) (mode=1) | 259.16 | 260.99 | 259.15 | 0.004 % |
Konvergenz %: 0.0 % Frequenz | Max P: 4 | Anz. Gleichungen: 60 | ||
mvsm007: 3D Zylinderförmige Auslegerschale
Analysetyp: | Modalanalyse |
Modelltyp: | 3D |
Vergleich: | Theoretische Ergebnisse |
Hintergrundinformation: | Roark, R.J., und Young, W.C. Formulas for Stress and Strain. NY: McGraw-Hill Co. 1982. S. 576. |
Beschreibung: | Ein Ausleger mit zylindrischer Schale wird symmetrisch als Halbzylinder modelliert. Ermitteln Sie die Grundfrequenz. |
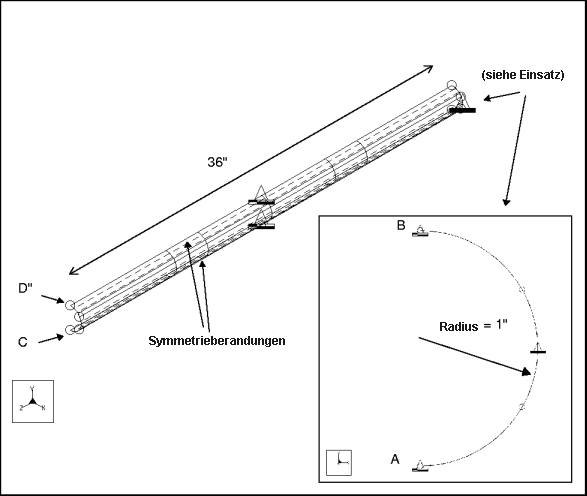
Spezifikationen
Art des Elements: | Schalenelement (3) | |
Einheiten: | IPS | |
Bemaßungen: | Länge: 36 Radius: 1 Dicke: 0.1 | |
Materialeigenschaften: | Massendichte: 7.28e4 Massenspezifische Materialkosten: 0 Elastizitätsmodul: 3e7 | Querkontraktionszahl: 0.3 Wärmeausdehnung: 0 Leitfähigkeit: 0 |
Randbedingung: | platziert auf Kante A-B: konstant in allen FG platziert auf Kante A-C, B-D: konstant in VerschX, RotY und RotZ | |
Vergleich der Ergebnisdaten
Theorie | Struktur | % Differenz | |
|---|---|---|---|
Frequenz (Hz) (mode=1) | 62.05 | 62.125 | 0.12% |
Konvergenz %: 0.4 % Frequenz | Max P: 6 | Anz. Gleichungen: 180 | |
mvsm008: 3D Volumenkörper Keilförmige Platte
Analysetyp: | Modalanalyse |
Modelltyp: | 3D |
Vergleich: | ANSYS No. 62 |
Hintergrundinformation: | Timoshenko, S., und Young, D.H. Vibration Problems in Engineering. 3. Ausgabe D. Van Nostrand Co., Inc. 1955. Seite 392, Art. 62. |
Beschreibung: | Ermitteln Sie die Grundfrequenz der Seitenschwingung einer keilförmigen Auslegerplatte. |
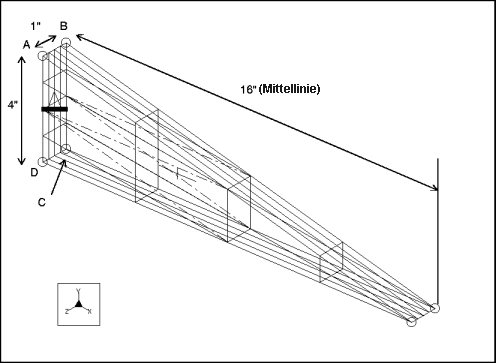
Spezifikationen
Art des Elements: | Volumenkörper (1) | |
Einheiten: | IPS | |
Bemaßungen: | Länge: 16 Breite: 4 Tiefe: 1 | |
Materialeigenschaften: | Massendichte: 7.28e–4 Massenspezifische Materialkosten: 0 Elastizitätsmodul: 3e7 | Querkontraktionszahl: 0 Wärmeausdehnung: 0 Leitfähigkeit: 0 |
Randbedingung: | platziert auf Fläche A-B-C-D: konstant in allen FG | |
Vergleich der Ergebnisdaten
Theorie | ANSYS | Struktur | % Differenz | |
|---|---|---|---|---|
Grundfrequenz (Hz) (mode=1) | 259.16 | 260.99 | 259.24 | 0.0 3 % |
Konvergenz %: 0.0 % Frequenz | Max P: 4 | Anz. Gleichungen: 72 | ||
mvsm009: 3D Schwingung in der Ebene eines an den Enden befestigten Kreuzes
Analysetyp: | Modalanalyse |
Modelltyp: | 3D |
Hintergrundinformation: | NAFEMS, SBNFA (November 1987), Test 1. |
Beschreibung: | Bestimmen Sie die ersten acht Eigenfrequenzen für die Schwingung in der Ebene eines Kreuzes, das an den Punkten A, B, C und D befestigt ist. |

Spezifikationen
Art des Elements: | Balken (4) | |
Einheiten: | NMS | |
Bemaßungen: | Länge: 5 | |
Balkeneigenschaften: | Fläche: 0.015625 IYY: 2.0345e–5 Schub FY: 0.83333 CY: 0.0625 | J: 4.069e–5 IZZ: 2.0345e–5 Schub FZ: 0.83333 CZ: 0.0625 |
Materialeigenschaften: | Massendichte: 8000 Massenspezifische Materialkosten: 0 Elastizitätsmodul: 2e11 | Querkontraktionszahl: 0.3 Wärmeausdehnung: 0 Leitfähigkeit: 0 |
Randbedingungen: | platziert auf den Punkten A, B, C, D: konstant in VerschX, VerschY und VerschZ platziert auf Balken A-O, B-O, C-O, D-O: konstant in VerschZ | |
Vergleich der Ergebnisdaten
Theorie | Struktur | % Differenz | |
|---|---|---|---|
Eigenfrequenz 1 (Hz) | 11.336 | 11.312 | 0.211% |
Eigenfrequenz 2 & 3 (Hz) | 17.709 | 17.636 | 0.412% |
Eigenfrequenz 4 (Hz) | 17.709 | 17.636 | 0.412% |
Eigenfrequenz 5 (Hz) | 45.345 | 45.155 | 0.419% |
Eigenfrequenz 6 & 7 (Hz) | 57.390 | 56.692 | 1.216% |
Eigenfrequenz 8 (Hz) | 57.390 | 57.001 | 0.677% |
Konvergenz %: 3.4 % Frequenz | Max P: 8 | Anz. Gleichungen: 157 | |
mvsm010: 3D Achsensymmetrische Schwingung einer ringförmigen Platte
Analysetyp: | Modalanalyse |
Modelltyp: | 3D |
Hintergrundinformation: | NAFEMS, SBNFA (November 1987), Test 53. |
Beschreibung: | Bestimmen Sie die ersten fünf Eigenfrequenzen für die achsensymmetrische Schwingung einer ringförmigen Platte. |
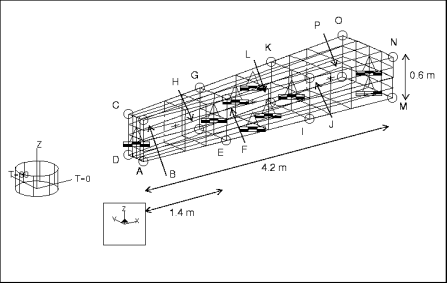
Spezifikationen
Art des Elements: | Volumenkörper (3) | |
Einheiten: | NMS | |
Bemaßungen: | Innenradius: 1.8 Außenradius: 6 Höhe: 0.6 | |
Materialeigenschaften: | Massendichte: 8000 Massenspezifische Materialkosten: 0 Elastizitätsmodul: 2e11 | Querkontraktionszahl: 0.3 Wärmeausdehnung: 0 Leitfähigkeit: 0 |
Randbedingungen: | Position | Freiheitsgrade |
|---|---|---|
constraint1 | platziert auf den Flächen ABCD, BCNO, ADMP, ABMN, CDPO, MNOP | konstant in VerschT, RotR und RotZ |
platziert auf Kurve MP | konstant in VerschZ |
Vergleich der Ergebnisdaten
Theorie | Struktur | % Differenz | |
|---|---|---|---|
Eigenfrequenz 1 (Hz) | 18.583 | 18.550 | 0.17 % |
Eigenfrequenz 2 (Hz) | 140.15 | 138.22 | 1.37% |
Eigenfrequenz 3 (Hz) | 224.16 | 224.16 | 0 % |
Eigenfrequenz 4 (Hz) | 358.29 | 355.80 | 0.7 % |
Eigenfrequenz 5 (Hz) | 629.19 | 620.43 | 1.4 % |
Konvergenz %: 1.3 % Frequenz | Max P: 9 | Anz. Gleichungen: 1094 | |