流动模型
“流动”(Flow) 模块可对质量守恒和动量求解,方法为使用瞬态纳维-斯托克斯方程 H.Ding, F.C. Visser, Y.Jiang, and M. Furmanczyk, “Demonstration and Validation of a 3-D CFD Simulation Tool Predicting Pump Performance and Cavitation for Industrial Applications,” FEDSM2009-78256, 2009.。
雷诺平均纳维-斯托克斯方程 (RANS) 的积分形式 (守恒) 如下所示:
• 连续性
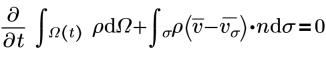
• 动量
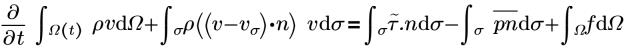
• 应力张量
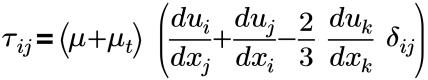
其中,
τij | 有效的剪应力 (分子+湍流) |
f | 体积力 |
n | 曲面法向 |
ρ | 静态压力 (Pa) |
t | 时间 |
v | 流体速度 |
vσ | 网格速度 |
Ω(t) | 控制体积与时间的函数 |
r | 平均局部流体密度 (kg/m3) |
σ | 控制体积曲面 |
µ | 动态黏度 (泊或 Pa-s) |
µt | 湍流动态黏度 |
δij | Kronecker delta 函数 (i=j 时为 1,i≠j 时为 0) |
黏度模型
动态黏度的值在“恒定动态黏度”(Constant Dynamic Viscosity) 选项下的框中指定。
• “恒定运动黏度”(Constant Dynamic Viscosity) - 指定选定体积块中的流体黏度。运动黏度的单位为 m2/s。运动黏度的值在“恒定运动黏度”(Constant Kinematic Viscosity) 选项下的框中指定。
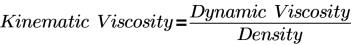
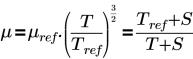
其中,
T | 温度 (K) |
µ参考 | 参考温度下的黏度 (Pa-s) |
S | Sutherland 温度 (K) |
T 是在能量模块处于非活动状态时需要作为输入的流体温度 (K)。 |
“Sutherland 定律”用于计算理想气体黏度与温度的函数关系。Sutherland, W. (1893), "The viscosity of gases and molecular force," Philosophical Magazine, S. 5, 36, pp. 507-531 (1893)。下表显示了选定气体的 Sutherland 恒定和参考温度。参考:en.wikipedia.org/wiki/viscosity。
气体 | S (K) | Tref (K) | mref (Pa-s) |
|---|---|---|---|
空气 | 120 | 291.15 | 18.27 e-6 |
氮气 | 111 | 300.55 | 17.81 e-6 |
氧气 | 127 | 292.25 | 20.81 e-6 |
二氧化碳 | 240 | 293.15 | 14.8 e-6 |
一氧化碳 | 118 | 288.15 | 17.2 e-6 |
氢气 | 72 | 293.85 | 8.76 e-6 |
氨气 | 370 | 293.15 | 9.82 e-6 |
二氧化硫 | 416 | 293.65 | 12.54 e-6 |
氦气 | 79.4 | 273 | 19 e-6 |
非牛顿黏度模型
非牛顿黏度模型包括:
• Herschel-Bulkley 模型
• Bingham 模型
这些模型为具有非牛顿流体属性的各种流体类型提供了相应黏度。Herschel-Bulkley 模型和 Bingham 模型将剪应力与剪切速率联系到一起,如下所示:
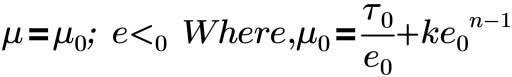
其中,
e0 | 临界剪切速率 |
k | 稠度指数 |
τ0 | 流体屈服应力 |
n | 幂次定律指数。对于 Bingham 模型,n=1 |
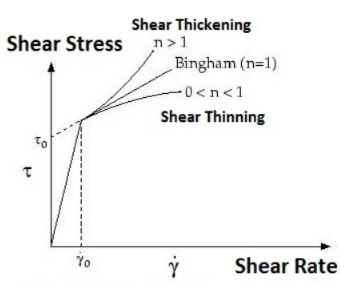
剪切速率 0 与上图中的 gamma 点相同。 |
流阻模型
• “压力损失”(Pressure Loss):基于以下方程:
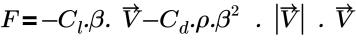
其中,
Cl | 线性阻力系数 (Pa-s/m2) |
Cd | 二次阻力系数 (1/m) |
β | 孔隙率 |
ρ | 密度 |
• “达西定律”(Darcy's Law):模型基于以下方程:
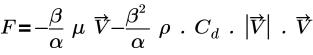
其中,
β | 孔隙率 |
α | 渗透率 |
µ | 动态黏度 |
V | 速度 |
Cd | 二次阻力系数 (1/m) |
流阻方程中使用的速度为局部速度。方程中 F 的测量单位为 N/m3,如力/体积、压力梯度 (Dp/Dx) 或 rg。界面的压力降通过将 F 与有限厚度相乘来计算。孔隙率在“通用”(Common) 模块中设置。