Physics
This section describes the theory and modeling in the module through the following topics:
Scalar Transport Equation
In the
Species module,
Creo Flow Analysis solves the transport equation for an arbitrary, user-defined scalar. For an arbitrary scalar,

, the general transport equation has the form:
where

,

and

are the user-specified diffusion coefficient, turbulent Schmidt number, and source term for the scalar

, respectively. Here,

is assumed to be isotropic. It can be a directly specified value or a user defined function.

is also indirectly determined through a specified Schmidt number which is a specified value or a user defined function. The turbulent Schmidt number,

, is a user-specified constant a default value of one. The source term
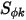
can be a constant or a user-defined function in the form of per-volume source or the total source in the computation domain.
Note that by selecting the module Species, only one scalar equation is added. For

-scalars, the module must be selected

times, and each species assigned a different name.
Equation 2.376 is a general scalar equation. It can be solved alone for a scalar transport, or as an addition to any or all of the standard modules. Since the diffusion and source terms are determined by user inputs of constant values or user-defined functions, the general scalar transport equation can be used to develop new physical models such as turbulence and combustion models. It can also be used in reduced forms that only consist of some of the terms in the equation. The examples are given below:
• Poisson and Laplace Equation
In the steady-state mode, if the convective flux is not solved or remains constant,
equation 2.376 is then reduced to a diffusion only problem:
Also, if the turbulent diffusion is ignored (
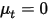
,or,
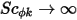
), and

is a constant,
equation 2.376 becomes a Poisson equation:
And when

, the scalar
equation 2.376 further added to a Laplace equation.
Among many applications, if
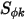
is replaced by the volume charge density (
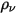
), and

is the permittivity (

), then
equation 2.376 can be applied to calculate electric potential (

) in an electric field:
• Convective Transport
Without the diffusion term (
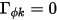
, and

, or

),
equation 2.376 is then reduced to:
Equation 2.376 can be used to model the transport of the phase volume fractions (

) in multiphase flows, in which the phases are immiscible (see
Multiphase module):
when
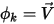
, and ⃗

, then
equation 2.376 represents the Euler equations for non-viscous flows:
Boundary Conditions
A user-defined scalar is any physical quantity. The boundary conditions, therefore, are not defined as the flow boundary conditions. For example, a flow inlet boundary may mean entirely something else for the scalar
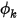
. As a result, for the general scalar transport equation, you can apply all the defined boundary types for the physical boundaries you select.
If
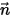
is a unit vector normal to the local boundary surface, the general expression of the per unit area mass flux is:
if the advection and diffusion are both present at the boundary.
For the scalar transport,

represents the flux per unit area that exits or enters the physical domain at a boundary. Depending on applications, the following common boundary conditions are derived from this general formulation:
• Zero Flux
Flux per unit area across (normal to) the boundary is specified at zero. With the condition of zero flux,

, the convective and diffusive fluxes must exactly balance:
This means that if one term is zero, the other term must also be zero. For example, at a solid (wall) boundary, the normal velocity to the surface is zero,

, though

may not be zero. To satisfy the constraint in
equation 2.376, the gradient of the scalar at the boundary must be zero,

.
In
Creo Flow Analysis, at a wall, zero flux is the default boundary condition for the scalar
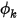
.
• Specified Value
Specified value is a boundary condition under which the value of the scalar at the boundary,

, is directly determined by a user input value of
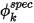
:
In
Creo Flow Analysis, at a flow inlet, specified constant value is the default boundary condition for
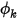
.
• Symmetry
For a symmetry boundary condition, zero normal-to-boundary gradient is applied for the scalar

:
In
Creo Flow Analysis, at a flow symmetry boundary, symmetry is also the default boundary condition for
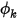
.
• Outlet
Outlet is used as a boundary condition at an opening where the flow is expected to exit or enter the domain. For a specified pressure outlet, or Resistor or Capacitor in the flow, this is the default condition for the scalar
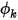
.
At an outlet boundary, the required input is the specified value for scalar

. The actual boundary condition applied for

depends on the flow conditions:
◦ Flow Leaving the Domain — When flow exits the computational domain from an outlet or at an inlet through reversed flow, zero-gradient is assumed at the boundary:
◦ Flow Entering the Domain — When flow enters the computational domain from an inlet or at an outlet through reversed flow, the specified value applies for the boundary:
• Convective Flux
At a boundary, the convective flux of

per unit area (

) is determined as a function of the external ambient value of the scalar (

) and an exchange coefficient (

):
where
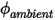
and

are user input parameters. Note that the exchange coefficient
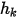
has the unit of

. From the known convective flux

, the boundary value of
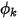
is obtained from
equation 2.376.
• Specified Scalar Flux
In this boundary condition, the flux of the scalar is specified in two ways:
◦ Flux per Area — In
equation 2.376, the scalar flux per unit area
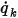
is specified by a user input as a constant value or user-defined function:
◦ Total Flux — Total scalar flux is known through a user input as a constant value or user-defined function:
where
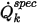
is the specified total scalar flux and

is the total boundary area. Then

is obtained from
equation 2.376 based on the flow conditions.
 , the general transport equation has the form:
, the general transport equation has the form: , the general transport equation has the form:
, the general transport equation has the form: , the general transport equation has the form:
, the general transport equation has the form:
 ,
,  and
and  are the user-specified diffusion coefficient, turbulent Schmidt number, and source term for the scalar
are the user-specified diffusion coefficient, turbulent Schmidt number, and source term for the scalar  , respectively. Here,
, respectively. Here,  is assumed to be isotropic. It can be a directly specified value or a user defined function.
is assumed to be isotropic. It can be a directly specified value or a user defined function.  is also indirectly determined through a specified Schmidt number which is a specified value or a user defined function. The turbulent Schmidt number,
is also indirectly determined through a specified Schmidt number which is a specified value or a user defined function. The turbulent Schmidt number,  , is a user-specified constant a default value of one. The source term
, is a user-specified constant a default value of one. The source term 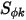 can be a constant or a user-defined function in the form of per-volume source or the total source in the computation domain.
can be a constant or a user-defined function in the form of per-volume source or the total source in the computation domain. -scalars, the module must be selected
-scalars, the module must be selected  times, and each species assigned a different name.
times, and each species assigned a different name.
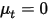 ,or,
,or,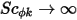 ), and
), and  is a constant, equation 2.376 becomes a Poisson equation:
is a constant, equation 2.376 becomes a Poisson equation:
 , the scalar equation 2.376 further added to a Laplace equation.
, the scalar equation 2.376 further added to a Laplace equation.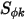 is replaced by the volume charge density (
is replaced by the volume charge density (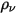 ), and
), and  is the permittivity (
is the permittivity ( ), then equation 2.376 can be applied to calculate electric potential (
), then equation 2.376 can be applied to calculate electric potential ( ) in an electric field:
) in an electric field:

 ) in multiphase flows, in which the phases are immiscible (see Multiphase module):
) in multiphase flows, in which the phases are immiscible (see Multiphase module):
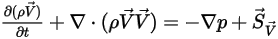
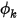 . As a result, for the general scalar transport equation, you can apply all the defined boundary types for the physical boundaries you select.
. As a result, for the general scalar transport equation, you can apply all the defined boundary types for the physical boundaries you select.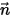 is a unit vector normal to the local boundary surface, the general expression of the per unit area mass flux is:
is a unit vector normal to the local boundary surface, the general expression of the per unit area mass flux is: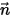
 represents the flux per unit area that exits or enters the physical domain at a boundary. Depending on applications, the following common boundary conditions are derived from this general formulation:
represents the flux per unit area that exits or enters the physical domain at a boundary. Depending on applications, the following common boundary conditions are derived from this general formulation: , the convective and diffusive fluxes must exactly balance:
, the convective and diffusive fluxes must exactly balance:
 , though
, though  may not be zero. To satisfy the constraint in equation 2.376, the gradient of the scalar at the boundary must be zero,
may not be zero. To satisfy the constraint in equation 2.376, the gradient of the scalar at the boundary must be zero,  .
.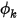 .
. , is directly determined by a user input value of
, is directly determined by a user input value of 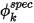 :
:
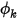 .
. :
:
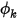 .
.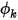 .
. . The actual boundary condition applied for
. The actual boundary condition applied for  depends on the flow conditions:
depends on the flow conditions:

 per unit area (
per unit area ( ) is determined as a function of the external ambient value of the scalar (
) is determined as a function of the external ambient value of the scalar ( ) and an exchange coefficient (
) and an exchange coefficient ( ):
):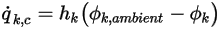
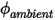 and
and  are user input parameters. Note that the exchange coefficient
are user input parameters. Note that the exchange coefficient 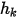 has the unit of
has the unit of  . From the known convective flux
. From the known convective flux  , the boundary value of
, the boundary value of 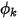 is obtained from equation 2.376.
is obtained from equation 2.376.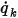 is specified by a user input as a constant value or user-defined function:
is specified by a user input as a constant value or user-defined function:
 is obtained based on the flow conditions.
is obtained based on the flow conditions.
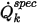 is the specified total scalar flux and
is the specified total scalar flux and  is the total boundary area. Then
is the total boundary area. Then  is obtained from equation 2.376 based on the flow conditions.
is obtained from equation 2.376 based on the flow conditions.