Modeling of Radiative Heat Transfer
In a thermal fluid system, the solid surfaces, fluid flow, or both the solid surfaces and fluid flow can be subjected to heating or cooling due to radiation. In CFA models, radiative heat transfer is explained by solving the Radiative Transport Equation (RTE) and then obtaining the radiative source term for the total energy conservation equation. A widely-used modeling approach, the Surface-to-Surface (S2S) radiation model, is the chosen model in Creo Flow Analysis.
Radiative Transfer Equation
As a ray of radiation traverses a layer of an absorbing, emitting, and scattering medium in a particular direction, the ray loses energy through both absorption and scattering away from the ray. The ray also gains energy from light sources in the medium through emission and the scattering directed towards the ray. The overall energy balance of the ray over an infinite layer of the medium results in a differential equation, known as the radiative transport equation (RTE).
To derive the radiative transport equation, consider that an incoming ray of radiation with the intensity of
I travels across a medium, for example, a gas, with the incremental thickness ds in the direction of
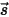
, as shown in
figure. Through the medium layer, the incidence at the location
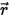
⃗ and direction

change in four ways, acting to either increase (energy gained +) or decrease (energy lost -) the radiation intensity

:
• Absorption—A medium, for example, gas, absorbs a fraction of the radiation traversing it. With the absorption coefficient
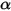
, the radiation energy lost through absorption is:
equation 2.282
• Scattering—A medium, for example, gas, scatters a fraction of the radiation energy to another direction (away from direction

) when the ray traverses the medium. With the scattering coefficient

, the radiation energy lost through scattering is:
Equation 2.283
• Emission—A medium emits radiation energy to the ray as a gray-body according to its local temperature (

) and emission characteristics to the ray. From Stefan-Boltzmann’s law and the reciprocity between emission and absorption,
equation 2.274 and
equation 2.279, the radiance emitted by the medium is:

Further, assuming that n is the refractive index of the medium (defined as the ratio of the velocity of light in vacuum to its velocity in the specified medium), the actual energy gained by the ray of radiation is:
Equation 2.284
• Scattering of Other Radiation—A fraction of other radiation sources in the layer of the medium is scattered into the ray of radiation dependent on the position and direction vectors
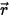
and

. Introducing
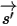

to represent the direction and solid angle of the radiation beam, and
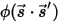
to be the phase function, you have the fraction of intensity of a ray traveling in all directions to be scattered to the direction of

⃗ as:
equation 2.285
With the incoming radiation

, and the outgoing radiation
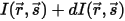
, the radiative energy balance in the direction

⃗ has the form:
equation 2.286
equation 2.287
The RTE is a first order integro-differential equation for the radiation intensity

in a fixed direction
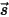
. To solve this equation within a domain, you need the temperature field within the domain, and you also require boundary conditions for
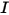
on both the internal and external surfaces, and also the interfaces between two different media.
The local medium temperature is obtained by solving the total energy (including the radiative sources) conservation equation, described in the
Heat module. For the thermal radiation, however, the boundary treatment is complex and depends on the radiation models. In general, a boundary can be an opaque medium that emits, reflects, and absorbs, or a semitransparent medium that also transmits. Reflection and transmission can be diffuse or specular or both diffuse and specular. For example, on an emitting and reflecting opaque boundary with gray radiation, and depending on the type of reflection, the intensity of a ray can be expressed as follows:
◦ Opaque boundary with diffuse emission and reflection:
Equation 2.288
◦ Opaque boundary with diffuse emission and specular reflection:
Equation 2.289
where,
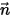 ⃗ | normal-to-surface unit vector at position  |
| direction and solid angle of a diffusely reflected ray (uniform reflection in all directions) |
| direction of the specularly reflected ray (perfect reflection depending on the incidence) |
| surface reflectivity, diffuse reflectivity and specular reflectivity, respectively which have the following relationship: equation 2.290 |
With the given boundary conditions,
equation 2.287 governs the transport of the radiation intensity in a specified direction. For gray radiations,
equation 2.287 should be solved in all the different directions within a sphere. For non-gray radiations, the intensity also depends on the wavelengths. Therefore, it needs to be solved in all directions over the entire spectrum of the wavelengths. Clearly, the direct solution of the radiative transfer equation is very time consuming. In many engineering simulations, therefore, it is desirable to use somewhat simplified yet approximate models to account for the directional and spectral dependencies. In CFD simulations, the following radiation models are routinely adopted, in which the detailed description may be found in references.
References: R. Siegel and J. R. Howell, Thermal Radiation Heat Transfer”, Hemisphere Publishing Corporation, Washington DC, 1992.
▪ Rosseland Radiation Model
References: R, Siegel and J. R. Howell, Thermal Radiation Heat Transfer”, Hemisphere Publishing Corporation, Washington DC, 1992.
▪ P-1 Radiation Model
References: R. Siegel and J. R. Howell, Thermal Radiation Heat Transfer, Hemisphere Publishing Corporation, Washington DC, 1992.
▪ Discrete Transfer Radiation Model
References: N. G. Shah, A New Method of Computation of Radiant Heat Transfer in Combustion Chambers”, PhD thesis, Imperial College of Science and Technology, London, England, 1979.
References: M. G. Carvalho, T. Farias, and P. Fontes, Predicting Radiative Heat Transfer in Absorbing, Emitting, and Scattering Media Using the Discrete Transfer Method”, In W. A. Fiveland et al., editor, Fundamentals of Radiation Heat Transfer, volume 160, pages 17-26. ASME HTD, 1991.
▪ Surface-to-Surface (S2S) Radiation Model
References: R. Siegel and J. R. Howell, Thermal Radiation Heat Transfer”, Hemisphere Publishing Corporation, Washington DC, 1992.
▪ Discrete Ordinates (DO) Radiation Model
References: G. D. Raithby and E. H. Chui, A Finite-Volume Method for Predicting a Radiant Heat Transfer in Enclosures with Participating Media”, J. Heat Transfer, 112:415-423, 1990.
References: E. H. Chui and G. D. Raithby, Computation of Radiant Heat Transfer on a Non-Orthogonal Mesh Using the Finite-Volume Method”, Numerical Heat Transfer, Part B, 23:269-288, 1993.
Each model has its own advantages and limitations regarding accuracy and cost. For example, while the Rosseland model does not solve a transport equation for the incident radiation. it is the fastest radiation model and requires the least extra memory. Rosseland can only be used for optically thick (optical thickness is the natural logarithm of the ratio of incident to transmitted radiant power in a medium) media due to its overly simplification of the radiative transport equation.
The discrete ordinates (DO) radiation model transforms
equation 2.287 into a transport equation for radiation intensity in the spatial coordinates
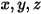
and solves it over a finite number of discrete solid angles associated with the vector direction
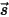
. The number of the solid angles selected directly determines the accuracy and the computational cost. The DO modeling approach is also identical to the approach used for the fluid flow and energy equations. At present, it is the most general radiation model that spans the entire range of optical thicknesses and can be applied to problems ranging from surface-to-surface radiation to participating radiation such as a combustion system. However, the computational cost of the DO model is high for non-gray radiations.
Among the above-mentioned radiation models, the surface-to-surface (S2S) radiation model is particularly good for modeling the enclosure radiative transfer without the consideration of the participating media. The typical examples are the radiative space heaters, and automotive underhood and underbody systems. In those situations, the radiation models for participating radiation are sometimes not efficient. As compared to the DO radiation model, the S2S model is faster per iteration, though the view factor calculation itself can be CPU-intensive. In Creo Flow Analysis, the current choice of model for radiative heat transfer is the S2S radiation model.
Surface-to-Surface (S2S) Radiation Model
The surface-to-surface radiation model accounts for the radiation exchange in an enclosure of gray-diffuse surfaces without participating media. The surface-to-surface radiative energy exchange depends on two main factors: the radiative characteristics of the involved surfaces, and the geometrical parameters including the surface areas and shapes, and the relative position to reach other (separation distance and orientation). In the S2S radiation model, the surface radiative heat transfer is considered by the gray-diffuse radiation model, while the geometrical parameters are accounted for by a geometric function referred to as view factor.
• Gray-Diffuse Radiation
The S2S radiation model assumes that the surfaces are gray and diffuse (gray radiation). For a gray surface, both emissivity
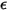
and absorptivity
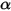
of the surfaces are independent of the wavelength of the outgoing and incoming rays. According to Kirchhoff’s law of thermal radiation in
equation 2.274, emissivity equals the absorptivity:
Equation 2.291
Also, with the assumption of a diffuse surface, no specular reflection occurs on the surface and the reflectivity (
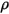
) of incident radiation at the surface is isotropic with respect to the solid angle. From
equation 2.290, surface reflectivity is determined as:
Equation 2.292
where,
| surface specular |
| diffuse reflectivity |
For a nonopaque or a semitransparent surface, transmissivity
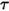
is also independent of the wavelengths:
Equation 2.293
The gray-diffuse surface-to-surface model assumes that the exchange of radiative energy between surfaces is virtually unaffected by the medium that separates them. Thus, if a certain amount of radiant energy
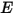
is incident on a surface per unit area (irradiance), the portions of the radiative energy reflected, absorbed, and transmitted are

,

and

respectively. Since for most applications, the surfaces are opaque to thermal radiation in the infrared spectrum, the radiative surfaces can be further considered as opaque. The transmissivity, therefore, can be neglected
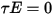
. From
equation 2.273 and
equation 2.274, the surface reflectivity
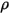
is expressed as:
Equation 2.294
with the assumptions of the surface gray-diffuse radiation, the S2S modeling equation is constructed based on energy conservation on each surface.
• S2S Modeling Equation
The main assumption of the S2S model is that in an enclosed system, the radiative heat transfer only occurs between gray-diffuse surfaces (gray radiation). You can ignore the absorption, emission, or scattering of radiation in the medium separating the surfaces. Therefore, only consider surface-to-surface radiation for numerical analysis.
The radiative energy flux leaving a given surface consists of directly emitted and reflected energy. The reflected energy flux is dependent on the incident energy flux from the surroundings, which then can be expressed in terms of the energy flux leaving all other surfaces. To compute the net radiative energy flow in a surface, it is convenient to define the radiosity
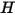
, which is the sum of the emissive power per unit area (emittance)

, and the reflected part of the radiation power received by the surface per unit area (irradiance)
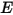
:
Equation 2.295
For an opaque surface,

, you have the radiosity:
equation 2.296
with the assumptions in S2S model, therefore, the following system of linear equations can be formulated to calculate the radiosity on each surface in an enclosed system. Assuming that

represents the radiosity on an arbitrary surface
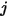
,
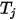
is the surface temperature, and
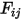
is the view factor between surface

and

, you have the radiosity in the surface

:
equation 2.297
where

is the number of the surfaces participating in the radiative heat transfer. Introducing the Kronecker symbol

and applying Stefan-Boltzmann’s law for gray radiation,
equation 2.278, you can rearrange
equation 2.297 and derive the S2S modeling equation:
equation 2.298
With the pre-calculated view factor

, the system of linear
equation 2.298 is solved to obtain

for the participating surfaces. Then the radiation net heat flows on each surface is computed easily. For the surface

, the net radiative heat flux

is the difference between the per-unit-area outgoing (
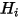
) and incoming (

) radiation. From
equation 2.278 and
equation 2.296, you can derive the following flux formulation:
Equation 2.299
For a given surface area
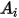
, the net radiation heat flows leaving the surface

is computed as:
Equation 2.300
The S2S model is composed of a system of linear equations in the form of
equation 2.298. The advantage in the application of the model is that for given view factors and temperatures, you calculate the net heat flows by solving a system of linear equations, which are computed by applying numerical algorithms. However, the main difficulty in applying the proposed surface-to-surface model is computation of the

view factors, for n-number of participating surfaces. This can be time consuming, in particular, with an increase in the number of surfaces.
Calculation of View Factor
In the S2S modeling
equation 2.298, the view factor

is the proportion of the radiation which leaves surface

and strikes surface

. As shown in
figure 2.37, assuming that

is the differential area on surface

, and
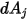
is the differential area on surface
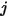
, and the distance between

and
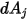
is

, you express the view factor
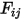
from

to

at a distance
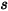
as follows:
Equation 2.301
where

and
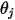
are the angle between the surface normal directions and a ray between the two differential areas.
Figure 2.37
If

and

are the given areas of surface

and
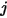
, respectively, the view factor from surface

to surface
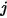
is the area averaged integral of
equation 2.301 over the surfaces

and
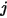
:
Equation 2.302
Note that surface-to-surface radiation only occurs when the two surfaces are visible to each other, or the view factor is non-zero. Introducing the Kronecker symbol

with respect to the visibility between
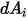
and

:
Equation 2.303
you can rewrite
equation 2.302 as:
Equation 2.304
For any two surfaces visible to each other, a given surface

only radiates a portion of the outgoing radiative energy to the surface
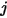
, as shown in
figure 2.378. Therefore, the dimensionless view factor
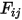
represents the portion of energy that leaves surface

and reaches surface

. The characteristics are in the list that follows:
Figure 2.378
• Summation of View Factors—Since radiation leaving a surface is conserved, the sum of all view factors from a given surface

is unity. For
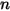
surface enclosed system, you have
Equation 2.305
• Self-Viewing Surfaces—Since radiation travels in straight lines, no radiation ray from a convex surface can leave the surface and then hit the same surface later. Hence, the convex surfaces cannot be self-viewed:
Equation 2.306
For concave surfaces, the outgoing ray from one position on the surface can hit the same surface later at a different position. Therefore, the concave surface can be visible to itself:
Equation 2.307
• Superposition—For
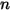
surface system, if a given surface

radiates to

number of surfaces (
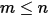
), then the view factor between the surface

and the

-number of surfaces equals the sum of the view factors between surface

and each one of the

-number of surfaces:
Equation 2.308
The superposition rule or summation rule is useful when a geometry is not available with given charts or graphs. With the superposition rule you can express the geometry that is being sought using the sum or difference of geometries that are known.
• Reciprocity—
Equation 2.304 defines the view factor
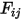
as the fraction of the radiative energy that leaves surface

and reaches surface

. Similarly, the view factor
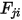
which is the portion of energy that leaves the surface
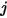
and reaches surface

is expressed as:
Equation 2.309
Equation 2.310
Equation 2.310 is referred to as the reciprocity of the view factors. With the reciprocity theorem you can directly calculate only one of the pair of view factors.
Clustering
The S2S radiation model is computationally expensive when the number of radiating surfaces is large. To reduce the computational time and the storage requirement, you can reduce the number of radiating surfaces by grouping a certain number of the neighboring boundary-cell faces to create surface clusters. The radiosity (
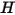
) is then calculated for surface clusters. These values are then distributed to the boundary-cell faces within each cluster to calculate the wall temperatures. Since the radiation source terms are highly nonlinear (proportional to the fourth power of temperature), make sure you calculate the average temperature of the surface clusters and distribute the flux and source terms appropriately among the boundary faces that form the clusters.
The surface cluster temperature is obtained by area-averaging of boundary face temperature as shown in the following equation:
Equation 2.311
where
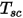
is the temperature of the surface cluster, and
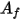
and

are the face area and temperature of the boundary cell in CFA simulations. The summation is carried over all the faces within a surface cluster.


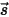 , as shown in figure. Through the medium layer, the incidence at the location
, as shown in figure. Through the medium layer, the incidence at the location 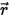 ⃗ and direction
⃗ and direction  change in four ways, acting to either increase (energy gained +) or decrease (energy lost -) the radiation intensity
change in four ways, acting to either increase (energy gained +) or decrease (energy lost -) the radiation intensity  :
: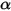 , the radiation energy lost through absorption is:
, the radiation energy lost through absorption is: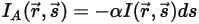
 ) when the ray traverses the medium. With the scattering coefficient
) when the ray traverses the medium. With the scattering coefficient  , the radiation energy lost through scattering is:
, the radiation energy lost through scattering is: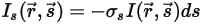
 ) and emission characteristics to the ray. From Stefan-Boltzmann’s law and the reciprocity between emission and absorption, equation 2.274 and equation 2.279, the radiance emitted by the medium is:
) and emission characteristics to the ray. From Stefan-Boltzmann’s law and the reciprocity between emission and absorption, equation 2.274 and equation 2.279, the radiance emitted by the medium is: 

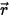 and
and  . Introducing
. Introducing 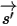
 to represent the direction and solid angle of the radiation beam, and
to represent the direction and solid angle of the radiation beam, and 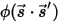 to be the phase function, you have the fraction of intensity of a ray traveling in all directions to be scattered to the direction of
to be the phase function, you have the fraction of intensity of a ray traveling in all directions to be scattered to the direction of  ⃗ as:
⃗ as:
 , and the outgoing radiation
, and the outgoing radiation 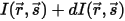 , the radiative energy balance in the direction
, the radiative energy balance in the direction  ⃗ has the form:
⃗ has the form: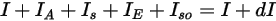
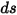 , gives the radiative transport equation (RTE) as follows:
, gives the radiative transport equation (RTE) as follows: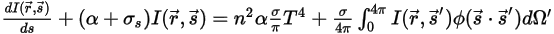
 in a fixed direction
in a fixed direction 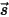 . To solve this equation within a domain, you need the temperature field within the domain, and you also require boundary conditions for
. To solve this equation within a domain, you need the temperature field within the domain, and you also require boundary conditions for 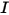 on both the internal and external surfaces, and also the interfaces between two different media.
on both the internal and external surfaces, and also the interfaces between two different media.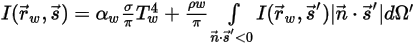

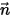 ⃗
⃗
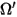



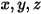 and solves it over a finite number of discrete solid angles associated with the vector direction
and solves it over a finite number of discrete solid angles associated with the vector direction 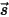 . The number of the solid angles selected directly determines the accuracy and the computational cost. The DO modeling approach is also identical to the approach used for the fluid flow and energy equations. At present, it is the most general radiation model that spans the entire range of optical thicknesses and can be applied to problems ranging from surface-to-surface radiation to participating radiation such as a combustion system. However, the computational cost of the DO model is high for non-gray radiations.
. The number of the solid angles selected directly determines the accuracy and the computational cost. The DO modeling approach is also identical to the approach used for the fluid flow and energy equations. At present, it is the most general radiation model that spans the entire range of optical thicknesses and can be applied to problems ranging from surface-to-surface radiation to participating radiation such as a combustion system. However, the computational cost of the DO model is high for non-gray radiations.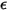 and absorptivity
and absorptivity 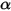 of the surfaces are independent of the wavelength of the outgoing and incoming rays. According to Kirchhoff’s law of thermal radiation in equation 2.274, emissivity equals the absorptivity:
of the surfaces are independent of the wavelength of the outgoing and incoming rays. According to Kirchhoff’s law of thermal radiation in equation 2.274, emissivity equals the absorptivity: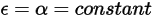
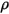 ) of incident radiation at the surface is isotropic with respect to the solid angle. From equation 2.290, surface reflectivity is determined as:
) of incident radiation at the surface is isotropic with respect to the solid angle. From equation 2.290, surface reflectivity is determined as:
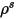

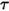 is also independent of the wavelengths:
is also independent of the wavelengths: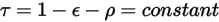
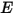 is incident on a surface per unit area (irradiance), the portions of the radiative energy reflected, absorbed, and transmitted are
is incident on a surface per unit area (irradiance), the portions of the radiative energy reflected, absorbed, and transmitted are  ,
,  and
and  respectively. Since for most applications, the surfaces are opaque to thermal radiation in the infrared spectrum, the radiative surfaces can be further considered as opaque. The transmissivity, therefore, can be neglected
respectively. Since for most applications, the surfaces are opaque to thermal radiation in the infrared spectrum, the radiative surfaces can be further considered as opaque. The transmissivity, therefore, can be neglected 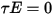 . From equation 2.273 and equation 2.274, the surface reflectivity
. From equation 2.273 and equation 2.274, the surface reflectivity 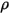 is expressed as:
is expressed as: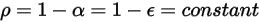
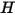 , which is the sum of the emissive power per unit area (emittance)
, which is the sum of the emissive power per unit area (emittance)  , and the reflected part of the radiation power received by the surface per unit area (irradiance)
, and the reflected part of the radiation power received by the surface per unit area (irradiance) 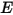 :
:
 , you have the radiosity:
, you have the radiosity:
 represents the radiosity on an arbitrary surface
represents the radiosity on an arbitrary surface 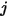 ,
, 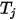 is the surface temperature, and
is the surface temperature, and 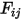 is the view factor between surface
is the view factor between surface  and
and  , you have the radiosity in the surface
, you have the radiosity in the surface  :
: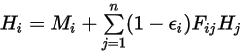
 is the number of the surfaces participating in the radiative heat transfer. Introducing the Kronecker symbol
is the number of the surfaces participating in the radiative heat transfer. Introducing the Kronecker symbol  and applying Stefan-Boltzmann’s law for gray radiation, equation 2.278, you can rearrange equation 2.297 and derive the S2S modeling equation:
and applying Stefan-Boltzmann’s law for gray radiation, equation 2.278, you can rearrange equation 2.297 and derive the S2S modeling equation: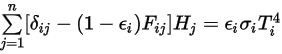
 , the system of linear equation 2.298 is solved to obtain
, the system of linear equation 2.298 is solved to obtain  for the participating surfaces. Then the radiation net heat flows on each surface is computed easily. For the surface
for the participating surfaces. Then the radiation net heat flows on each surface is computed easily. For the surface  , the net radiative heat flux
, the net radiative heat flux  is the difference between the per-unit-area outgoing (
is the difference between the per-unit-area outgoing (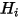 ) and incoming (
) and incoming ( ) radiation. From equation 2.278 and equation 2.296, you can derive the following flux formulation:
) radiation. From equation 2.278 and equation 2.296, you can derive the following flux formulation: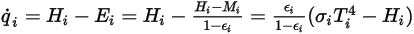
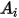 , the net radiation heat flows leaving the surface
, the net radiation heat flows leaving the surface  is computed as:
is computed as:
 view factors, for n-number of participating surfaces. This can be time consuming, in particular, with an increase in the number of surfaces.
view factors, for n-number of participating surfaces. This can be time consuming, in particular, with an increase in the number of surfaces. is the proportion of the radiation which leaves surface
is the proportion of the radiation which leaves surface  and strikes surface
and strikes surface  . As shown in figure 2.37, assuming that
. As shown in figure 2.37, assuming that  is the differential area on surface
is the differential area on surface  , and
, and 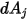 is the differential area on surface
is the differential area on surface 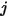 , and the distance between
, and the distance between  and
and 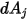 is
is  , you express the view factor
, you express the view factor 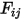 from
from  to
to  at a distance
at a distance 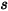 as follows:
as follows:
 and
and 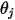 are the angle between the surface normal directions and a ray between the two differential areas.
are the angle between the surface normal directions and a ray between the two differential areas.
 and
and  are the given areas of surface
are the given areas of surface  and
and 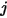 , respectively, the view factor from surface
, respectively, the view factor from surface  to surface
to surface 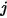 is the area averaged integral of equation 2.301 over the surfaces
is the area averaged integral of equation 2.301 over the surfaces  and
and 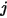 :
:
 with respect to the visibility between
with respect to the visibility between 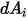 and
and  :
: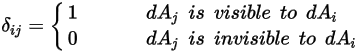

 only radiates a portion of the outgoing radiative energy to the surface
only radiates a portion of the outgoing radiative energy to the surface 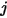 , as shown in figure 2.378. Therefore, the dimensionless view factor
, as shown in figure 2.378. Therefore, the dimensionless view factor 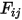 represents the portion of energy that leaves surface
represents the portion of energy that leaves surface  and reaches surface
and reaches surface  . The characteristics are in the list that follows:
. The characteristics are in the list that follows: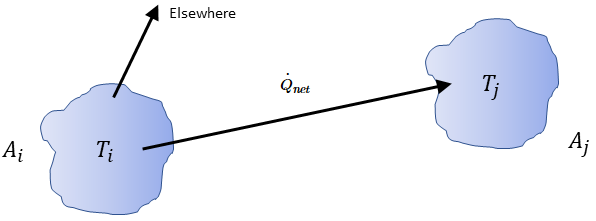
 is unity. For
is unity. For 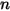 surface enclosed system, you have
surface enclosed system, you have


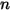 surface system, if a given surface
surface system, if a given surface  radiates to
radiates to  number of surfaces (
number of surfaces (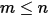 ), then the view factor between the surface
), then the view factor between the surface  and the
and the  -number of surfaces equals the sum of the view factors between surface
-number of surfaces equals the sum of the view factors between surface  and each one of the
and each one of the  -number of surfaces:
-number of surfaces:
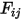 as the fraction of the radiative energy that leaves surface
as the fraction of the radiative energy that leaves surface  and reaches surface
and reaches surface  . Similarly, the view factor
. Similarly, the view factor 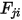 which is the portion of energy that leaves the surface
which is the portion of energy that leaves the surface 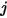 and reaches surface
and reaches surface  is expressed as:
is expressed as:

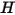 ) is then calculated for surface clusters. These values are then distributed to the boundary-cell faces within each cluster to calculate the wall temperatures. Since the radiation source terms are highly nonlinear (proportional to the fourth power of temperature), make sure you calculate the average temperature of the surface clusters and distribute the flux and source terms appropriately among the boundary faces that form the clusters.
) is then calculated for surface clusters. These values are then distributed to the boundary-cell faces within each cluster to calculate the wall temperatures. Since the radiation source terms are highly nonlinear (proportional to the fourth power of temperature), make sure you calculate the average temperature of the surface clusters and distribute the flux and source terms appropriately among the boundary faces that form the clusters.
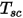 is the temperature of the surface cluster, and
is the temperature of the surface cluster, and 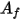 and
and  are the face area and temperature of the boundary cell in CFA simulations. The summation is carried over all the faces within a surface cluster.
are the face area and temperature of the boundary cell in CFA simulations. The summation is carried over all the faces within a surface cluster.