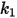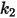Particle Erosion Modeling
Erosion is a phenomenon that causes loss of material due to repeated impact of solid particles on a surface. Erosion damages pipes, valves, and other flow passages. It is therefore important to study the erosion rate and identify areas susceptible to erosion in the flow passages.
CFA-based erosion modeling includes the following steps:
1. Flow field data such as velocity is obtained by solving the Navier-Stokes equations.
2. Particles are released within the flow field and individually tracked to obtain information such as impact velocity and impact angle.
3. The impact information of particles is used in an erosion equation to compute erosion ratio/rate or surface mass loss caused by the impacting particles.
Erosion equations study the effects of various parameters on erosion such as:
References: Mazdak Parsi et al. “A comprehensive review of solid particle erosion modeling for oil and gas wells and pipelines applications” (2014)
• Particle characteristics such as size, shape, density, hardness, and so on
• Particle impact information such as particle impact velocity
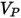
, impact angle

, particle-particle interaction, and so on
• Target wall properties such as material density, hardness, and so on
The erosion equations compute the erosion ratio
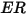
, defined as the amount of wall material loss (due to impact of solid particles) divided by the mass of the impacting solid particles.
Creo Flow Analysis uses the erosion models detailed in the following sections:
References: Mazdak Parsi etc. “CFD simulation of sand particle erosion in gas-dominant multiphase flow” (2015)
Finne Model
The erosion equation of Finne is as follows:
where,
| wall material density (kg/m3) |
| particle impact velocity (m/s) |
| velocity exponent (equal to 2 for most industrial applications) |
| Vicker hardness (Pa) |
| angle of impact (deg) |
|  This model underestimates material removal for particle impact angles greater than  and no erosion is predicted for normal impacts. |
Zhang model
The erosion equation of Zhang is as follows:
where,
| erosion ratio |
| |
| Brinell hardness of the wall material (Pa) |
| particle shape factor |
| particle impact velocity (m/s) |
| velocity exponent (equal to 2.41) |
| impact angle function |
The particle shape factor

has the following values for different types of sand particles:
Value | Type of sand particle |
1.0 | sharp or angular |
0.53 | semirounded |
0.2 | fully rounded |
The impact angle function is given as follows:
The following table lists the values of

:
Oka Model
The erosion equation of Oka et al. is as follows:
Equation 2.406
Equation 2.407
Equation 2.408
Equation 2.409
Equation 2.410
where,
| volumetric erosion rate (mm3/kg) |
| erosion damage at a normal impact angle (mm3/kg) |
| reference impact velocity (m/s) |
| particle diameter (m) |
| reference particle diameter (m) |
| Vicker hardness (GPa) |
The values of different coefficients used in
equation 2.406,
equation 2.407,
equation 2.408,
equation 2.409, and
equation 2.410 appear in the following table:
| | | | | | |
60 | -0.12 | 0.19 | 0.71 | 2.4 | 0.14 | -0.94 |
DNV Model
The erosion equation of DNV is as follows:
where,
| |
 (velocity exponent) | |
The table below lists the values of

:
| | | | | | | |
9.370 | -42.295 | 110.864 | -175.804 | 170.137 | -98.398 | 31.211 | -4.170 |
Mansouri Model
Mansouri developed an erosion equation as follows:
Equation 2.413
Equation 2.414
where,
| erosion ratio |
| Brinell hardness of the wall material (Pa) |
| particle shape factor |
| particle impact velocity (m/s) |
| velocity exponent |
| impact angle function |
| Vicker hardness (Pa) |
| Angle of impact (deg) |
The following table contains the values of different parameters used in
equation 2.413 and
equation 2.414 of Mansouri (2015) erosion equation.
| | | | | |
0.6947 | 2.41 | 0.2 | 0.85 | 0.65 | 4.49e-07 |
Grant-Tabakoff model
The erosion equation of the Grant-Tabakoff model is as follows:
Equation 2.415
where,
Equation 2.416
where,
| erosion ratio |
| particle impact velocity (m/s) |
| angle of impact (deg) |
| angle of maximum erosion (deg) |
Erosion rate
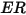
in
equation 2.415, is defined as the amount, in milligram, of material removed per unit of mass (gram) of impacting particles. The unit of velocity is ft/s.
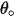
is the angle of maximum erosion. For example,

for aluminum-based alloy.
The values of different coefficients for the Grant-Tabakoff model are in the following table::
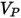 , impact angle
, impact angle  , particle-particle interaction, and so on
, particle-particle interaction, and so on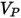 , impact angle
, impact angle  , particle-particle interaction, and so on
, particle-particle interaction, and so on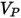 , impact angle
, impact angle  , particle-particle interaction, and so on
, particle-particle interaction, and so on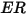 , defined as the amount of wall material loss (due to impact of solid particles) divided by the mass of the impacting solid particles.
, defined as the amount of wall material loss (due to impact of solid particles) divided by the mass of the impacting solid particles.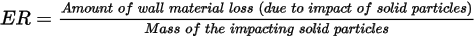

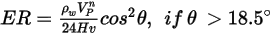


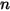
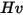

 and no erosion is predicted for normal impacts.
and no erosion is predicted for normal impacts.

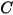



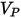


 has the following values for different types of sand particles:
has the following values for different types of sand particles:
 :
:





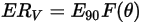



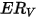
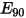

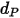





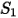


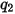
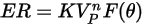


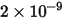
 (velocity exponent)
(velocity exponent)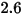
 :
:





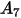
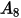






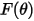

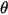
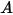

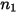






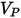
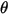
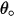
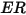 in equation 2.415, is defined as the amount, in milligram, of material removed per unit of mass (gram) of impacting particles. The unit of velocity is ft/s.
in equation 2.415, is defined as the amount, in milligram, of material removed per unit of mass (gram) of impacting particles. The unit of velocity is ft/s.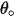 is the angle of maximum erosion. For example,
is the angle of maximum erosion. For example,  for aluminum-based alloy.
for aluminum-based alloy.