Spezifische Überlegungen zum VOF-Modell (Volume of Fluid)
VOF-Modell im Vergleich zum Mischungs-Modell
Im homogenen Eulerschen Mehrphasenmodellierungsansatz lösen sowohl die VOF-Modelle (Volume of Fluid) als auch die Eulerschen Mischungsmodelle den gleichen Satz von zugrunde liegenden Gleichungen für die Mischung (gemittelt). Allerdings basieren Sie auf verschiedenen physikalischen Mechanismen und gelten für verschiedene Mehrphasenflussmodelle.
• Mischungsmodell – Konzipiert für zwei oder mehr Phasen (Flüssigkeit oder Partikel), die als einander durchdringende Kontinua behandelt werden. Es löst die Impulsgleichung und die Energiegleichungen für die Mischung und die Schnittstelle von Phase zu Phase wird nicht verfolgt und es werden keine klaren Schnittstellen beobachtet. Anwendungen des Mischungsmodells sind u. a. partikelbeladene Flüsse mit geringer Last, Blasen- und Tröpfchenflüsse, Sedimentation und Zyklonabscheider. Sie können das Mischungsmodell auch mit vorgegebenen relativen Geschwindigkeiten für die dispergierten Phasen verwenden, um inhomogene Mehrphasenflüsse zu modellieren.
• VOF-Modell – Allgemein gesehen eine transiente Oberflächenverfolgungstechnik für zwei oder mehr unvermischbare Flüssigkeiten, bei denen die Position der Schnittstelle von Phase zu Phase von Interesse ist. Im VOF-Modell wird ein einziger Satz von Impuls- und -Energiegleichungen für die Mischung von allen Phasen gemeinsam genutzt und implizit gelöst. Die Phasen-Volumen-Anteile werden unter Verwendung genauer expliziter oder impliziter Zeitalgorithmen mit Advektionsschemen höherer Ordnung ermittelt, um scharfe Schnittstellen zwischen einem Phasenpaar zu lösen. Typische Anwendungen des VOF-Modells sind u. a. geschichtete Flüsse, Flüsse mit freier Oberfläche, Füllung, Schwappen, die Bewegung großer Blasen in einer Flüssigkeit, die Bewegung von Flüssigkeit nach einem Dammbruch, die Prognose des Strahlzerfalls (Oberflächenspannung) und die Verfolgung von Flüssigkeit-Gas-Schnittstellen.
Die VOF-Formel basiert auf der Tatsache, dass zwei oder mehr Flüssigkeiten (oder Phasen) einander nicht durchdringen. In einer gegebenen Steuervolumenzelle kann daher mit den lokalen Phasen-Volumen-Anteilen allein bestimmt werden, ob diese nur eine der Phasen oder eine Phasenmischung enthält. Beispielsweise sind für die q-te Phase, wenn der Volumenanteil in einer Zelle αq ist, nur die folgenden drei Bedingungen möglich:
◦ αq = 0: Die Zelle enthält die q-te Phase nicht
◦ αq = 1: Die Zelle ist voll mit der q-ten Phase
◦ 0< αq < 1: Die Zelle enthält die Schnittstelle zwischen der q-ten Phase und einer oder mehreren anderen Phasen.
Daher können Sie die Verfolgung der Schnittstellen zwischen den Phasen mit der Lösung einer Transportgleichung für den Volumenanteil von einer oder mehreren der Phasen durchführen.
Der Effekt der Oberflächenspannung
Die Oberflächenspannung ist die elastische Neigung der Oberfläche einer Flüssigkeit, ihren Flächeninhalt möglichst klein zu halten. Betrachten Sie eine Luftblase in einer Flüssigkeit. Innerhalb der Blase ist die resultierende Kraft der Nachbarmoleküle auf ein Molekül gleich null. An Schnittstellen von Flüssigkeit und Luft resultiert die Oberflächenspannung daraus, dass die gegenseitige Anziehungskraft der Flüssigkeitsmoleküle aufgrund von Kohäsion größer ist als zu Molekülen in der Luft aufgrund von Adhäsion. Daraus resultiert eine radiale nach innen gerichtete Kraft an ihrer Oberfläche, die dazu führt, dass sich die Blase zusammenzieht. Der Druck innerhalb der Blase nimmt zu, um die zwischenmolekularen Anziehungskräfte auszugleichen.
• Das Kontinuum-Flächenkraftmodell
In
Creo Flow Analysis kann das VOF-Modell die Effekte der Oberflächenspannung entlang der Schnittstelle zwischen jedem Phasenpaar einschließen. Das übernommene Oberflächenspannungsmodell beruht auf dem Kontinuum-Flächenkraftmodell (Continuum Surface Force, CFS) von Brackbill et al. Bei diesem Ansatz wird der Oberflächenspannungseffekt als eine zusätzliche volumetrische Kraft betrachtet, die an der Schnittstelle konzentriert ist, und nicht eine Oberflächenkraft ist. Bei der freien Oberflächenschnittstelle, die in
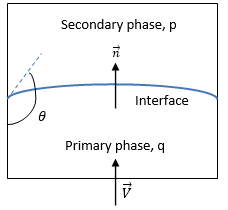
Abbildung 2.26 dargestellt wird, ist die primäre Flüssigkeit die Phase q (die Flüssigphase) und die sekundäre Flüssigkeit ist die Phase p (normalerweise eine Gasphase). Gemäß dem Kontinuum-Flächenkraftmodell wird die Flächenkrümmung aus den lokalen Gradienten in der Flächennormalen an der Schnittstelle berechnet. Es sei angenommen, dass
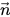
der Flächennormalenvektor ist, definiert als Gradient des primären Flüssigkeitsvolumenanteils α
q:
Die Schnittstellenkrümmung k ist hinsichtlich der Divergenz den Normalenvektors der Einheit definiert:
Gleichung 2.93
Hierbei ist
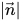
der Betrag des Vektors
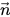
.
Die Oberflächenspannungskraft an der Fläche wird als volumetrische Kraft unter Verwendung des Divergenztheorems ausgedrückt, ein zusätzlicher Quellenausdruck, der zur Impulsgleichung der Mischung hinzugefügt wird:
Gleichung 2.94
Hierbei ist σ
qp der Oberflächenspannungskoeffizient zwischen Flüssigkeit q und Flüssigkeit p. Er hat die Einheit N/m. Die
Gleichung 2.94 ermöglicht eine glatte Überlagerung von Kräften nahe Zellen, bei denen mehr als zwei Phasen vorhanden sind. Wenn nur zwei Phasen in einer Zelle vorhanden sind, bestehen die folgenden Beziehungen:
Gleichung 2.95
Hierbei ist ρ die Mischungsdichte. Dann wird
Gleichung 2.94 verkürzt auf
Gleichung 2.96
• Einbeziehen die Oberflächenspannungskraft
Die Bedeutung von Oberflächenspannungseffekte wird durch zwei dimensionslose Parameter bestimmt: die Reynolds-Zahl Re und die Kapillarzahl Ca oder die Reynolds-Zahl und die Weber-Zahl We:
Wenn Re<<1 ist der Parameter von Interesse die Kapillarzahl:
Gleichung 2.97
Hierbei ist U∞ die freie Strömungsgeschwindigkeit. Die Oberflächenspannungseffekte werden vernachlässigt, wenn Ca>>1, da die Oberflächenspannungskraft zu klein ist.
Wenn Re>>1, ist der Parameter von Interesse die Weber-Zahl:
Gleichung 2.98
Hierbei ist l die charakteristische Länge. Die Oberflächenspannungseffekte können auch vernachlässigt werden, wenn We>>1, wenn die Trägheitskraft deutlich größer als die Oberflächenspannungskraft ist.
Wandadhäsion (Kontaktwinkel)
Das VOF-Modell (Volume of Fluid) bietet eine Option, um einen Wandadhäsionswinkel in Verbindung mit dem Oberflächenspannungsmodell anzugeben. Gemäß Brackbill et. al. wird der Kontaktwinkel zwischen Flüssigkeit und Wand an der Schnittstelle verwendet, um die Flächennormale in Zellen in Wandnähe anzupassen, anstatt diese Randbedingung direkt auf die Wand anzuwenden. Diese sogenannte dynamische Randbedingung führt zur Anpassung der Krümmung der Fläche in Wandnähe.
Wenn θ der Kontaktwinkel der Schnittstelle der freien Oberfläche an der Wand ist, wie in
Abbildung 2.26 dargestellt, dann wird der Normalenvektor an der wandnahen Zelle wie folgt berechnet ist:
Gleichung 2.99
Dabei gilt:
| Einheitsvektor senkrecht zur Wand |
| Einheitsvektor tangential zur Wand |
Anschließend wird die berechnete Geschwindigkeit
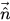
des Einheitsvektors verwendet, um die lokale Krümmung der Fläche zu bestimmen,
Gleichung 2.93, und im Anschluss daran die Oberflächenspannungskraft,
Gleichung 2.94 oder
Gleichung 2.95.
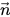 der Flächennormalenvektor ist, definiert als Gradient des primären Flüssigkeitsvolumenanteils αq:
der Flächennormalenvektor ist, definiert als Gradient des primären Flüssigkeitsvolumenanteils αq: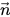 der Flächennormalenvektor ist, definiert als Gradient des primären Flüssigkeitsvolumenanteils αq:
der Flächennormalenvektor ist, definiert als Gradient des primären Flüssigkeitsvolumenanteils αq: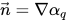
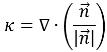
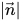 der Betrag des Vektors
der Betrag des Vektors 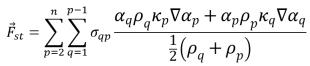
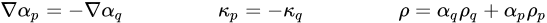
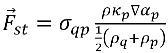
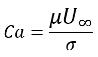
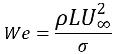
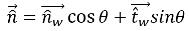
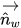
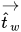
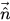 des Einheitsvektors verwendet, um die lokale Krümmung der Fläche zu bestimmen,
des Einheitsvektors verwendet, um die lokale Krümmung der Fläche zu bestimmen,