Bewegungen eines Starrkörpers
In Simulationen sind die Flächen eines Volumenkörperobjekts normalerweise Wandberandungen in einer Strömungsdomäne. Wenn ein Volumenkörperobjekt oder eine Fläche dynamischen und mechanischen Kräften und einer thermischen Wirkung ausgesetzt ist, kann das Ungleichgewicht der Nettokräfte dazu führen, dass sich der Körper bewegt und verformt. Ein Volumenkörperobjekt wird in Fluss-Simulationen häufig als Starrkörper betrachtet. Daher wird für ein Volumenkörperobjekt, das Kraftungleichgewichten ausgesetzt ist, davon ausgegangen, dass es linear (Translation), radial (Rotation) oder sowohl linear als auch radial ohne Verformung bewegt werden kann. Bei einer CFA-Rechendomäne kann die Berandungsbewegung jedoch zur Domänenänderung führen, und daher kann sich das Volumennetz verformen, wie im Modul
Flow beschrieben.
Für einen Starrkörper werden die Gleichungen, die für seine Bewegungen gelten, direkt aus der Erhaltung des linearen Impulses und des Drehimpulses abgeleitet:
• Linearer Impuls (Translation)
Gleichung 2.426
• Drehimpuls (Rotation)
Gleichung 2.427
In
Gleichung 2.426 ist
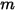
die Masse des sich bewegenden Objekts;
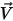
⃗ ist die lineare/translatorische Geschwindigkeit; und
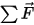
⃗ sind die Gesamt-/Nettokräfte, die auf den Körper unter der Translation ausgeübt werden. In
Gleichung 2.427 ist
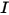
das Trägheitsmoment;
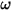
⃗ ist die Winkelgeschwindigkeit; und
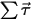
⃗ ist das Gesamt-/Netto-Drehmoment, das auf den rotierenden Körper wirkt.
Gleichung 2.426 und
Gleichung 2.427 gelten für die allgemeinen Bewegungen eines Volumenkörpers, die sechs Freiheitsgrade (6-DOF) mit jeweils drei Graden für Translation (3-DOF) und Rotation (3-DOF) haben.
Creo Flow Analysis berücksichtigt nur 1-FG-Translation und -Rotation, die in diesem Abschnitt erläutert werden.
1-FG-Translation
Unter der Annahme, dass sich ein Volumenkörper linear in eine beliebig angegebene Richtung bewegt (bleibt unverändert), definiert durch einen Einheitsvektor
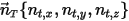
, wird die translatorische Bewegung des Körpers auf einen Freiheitsgrad (1-DOF) reduziert. Anschließend wird
Gleichung 2.426 zur linearen Impulserhaltung zu einer skalaren Gleichung entlang der Bewegungsrichtung, da die Bewegungsgeschwindigkeit und -kraft in Bezug auf
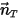
ausgedrückt werden:
Gleichung 2.428
Gleichung 2.429
Gleichung 2.430
Dabei ist
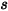
der Betrag des Positionsvektors
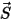
an einem Punkt von Interesse auf dem Volumenkörper entlang der Bewegungsrichtung

. In einem kartesischen Koordinatensystem gilt
Gleichung 2.431
Wenn die Masse des Volumenkörpers konstant bleibt und der Kraftterm so erweitert wird, dass explizit alle auf den Körper angewendeten Kräfte eingeschlossen werden, ergibt sich als skalare lineare Impulsgleichung:
Gleichung 2.432
Die Kräfte auf der rechten Seite geben Folgendes an:
• Strömungskraft

– Besteht aus Druck- und Schubkräften. Sie werden durch die relative Bewegung zwischen dem Flüssigkeitsfluss und den Flächen des Volumenkörpers verursacht, die in Kontakt mit dem Fluss stehen. Die Druck- und Schubkräfte werden aus den Flow-Lösungen (Ausgabemengen) ermittelt:
Gleichung 2.433
• Dämpfungskraft
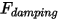
– Eine Verzögerungskraft, die durch die Reibungsdämpfungswirkung verursacht wird. Sie wird durch die Bewegung des Volumenkörperobjekts und den benutzerdefinierten Dämpfungskoeffizienten

bestimmt:
Gleichung 2.434
• Federkraft

– Ist abhängig von der Federverschiebung
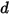
, der Federkonstante
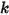
und der Federvorspannkraft
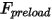
:
Gleichung 2.435
Dabei ist die Federverschiebung

definiert als:
Gleichung 2.436
Dabei ist

der Betrag des Positionsvektors
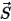
an der vorherigen Position
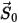
.
• Reibungskraft – Das Kontaktreibungsmodell wird übernommen, um die Wirkung der Reibung in einem dynamischen System zu berücksichtigen. Die Reibungskraft
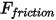
wird modelliert als:
Gleichung 2.437
Dabei ist
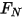
die Normalkomponente der Kontaktkraft, die auf die Körperfläche von Interesse ausgeübt wird. Für den Reibungskoeffizienten
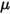
werden der Haftreibungskoeffizient
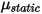
und der Gleitreibungskoeffizient
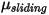
weiter für die stationären bzw. sich bewegenden Körper eingeführt:
Gleichung 2.438
• Zusätzliche Kraft
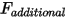
– Für zusätzliche benutzerdefinierte Kräfte hinzugefügt.
1-FG-Rotation
Wenn eine beliebige rotierende Achse durch einen Punkt (Mittelpunkt der Achse)
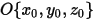
und den Richtungseinheitsvektor

definiert ist, wird die Rotation des Volumenkörpers um die Achse
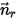
ebenfalls auf eine 1-FG-Rotation reduziert. Entsprechend wird
Gleichung 2.427 zur Drehimpulserhaltung ebenfalls zu einer skalaren Gleichung entlang der tangentialen Richtung
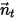
, definiert als:
Gleichung 2.439
Dabei ist
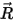
der Vektor, der vom Mittelpunkt der Achse zu einem beliebigen Punkt

auf dem Volumenkörper zeigt:
Gleichung 2.440
Die Winkelgeschwindigkeit und das Drehmoment am Punkt

werden umformuliert als:
Gleichung 2.441
Gleichung 2.442
Gleichung 2.443
Dabei ist
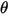
der Rotationswinkel des Punkts
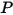
relativ zur Start- oder Referenzposition.
Wenn das Trägheitsmoment konstant bleibt und der Kraftterm so erweitert wird, dass explizit alle auf den Körper angewendeten Drehmomente eingeschlossen werden, ergibt sich als skalare Drehimpulsgleichung:
Gleichung 2.444
Die Drehmomentterme auf der rechten Seite sind wie folgt definiert:
• Hydrodynamisches Drehmoment

– Kombination des Drehmoments aufgrund von Druck- und Schubkräften:
Gleichung 2.445
• Dämpfungsmoment
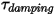
– Hängt von der Rotationsgeschwindigkeit
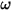
und dem benutzerdefinierten Dämpfungskoeffizienten
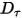
ab:
Gleichung 2.446
• Federdrehmoment
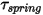
– Drehmoment induziert durch Torsion, die vom Verschiebungswinkel
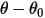
, vom benutzerdefinierten Vorspannungsmoment

und von der Torsionskonstante

abhängt.
Gleichung 2.447
Dabei ist

der Referenzwinkel. Dieser ist in der Regel die Position der Berandung oder des Volumens während des Modell-Setups, kann jedoch einer anderen Position entsprechen. Bei einer Nullwinkelverschiebung ist der Referenzwinkel

beispielsweise nicht gleich der Anfangswinkelposition.
• Reibungsdrehmoment – Drehmoment, das durch die Reibungskraft entsteht, die bei der Bewegung zweier Objekte in Kontakt auftritt. In Experimenten wird dieses durch die Differenz zwischen dem angewendeten Drehmoment und dem beobachteten oder Netto-Drehmoment bestimmt. Es ist abhängig vom Reibungskoeffizienten
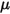
und dem Kontaktmoment aus der Anwendung der Normalkraft
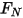
auf die Kontaktfläche:
Gleichung 2.448
Dabei ist
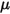
ein benutzerdefinierter Parameter, der in
Gleichung 2.438 definiert ist.
• Zusätzliche Drehmomente
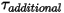
– Für zusätzliche benutzerdefinierte Drehmomente hinzugefügt.
Ablenkungsmodell
In vielen Situationen wird ein Volumenkörper nur in einem begrenzten Raum (begrenzter Abstand oder Winkel) verschoben oder rotiert oder sowohl verschoben als auch rotiert, d.h. er hat eine maximale, minimale oder sowohl eine maximale als auch eine minimale Position. Beispiel: Wenn, wie in der folgenden
Abbildung gezeigt, ein einfaches Schwerkraftpendel von der ursprünglichen Position mit dem Winkel

freigegeben wird, verursacht die auf seine Masse wirkende Rückstellkraft, dass es um die Gleichgewichtsposition herum schwingt. Der maximale Winkel auf jeder der Seiten der Gleichgewichtsposition
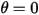
hängt von seiner Freigabeposition

ab. Wenn keine Reibung (reibungsfreier Drehpunkt und Vakuum) vorhanden ist, bleibt der maximale Winkel unverändert, und das Pendel schwingt dauerhaft zwischen denselben Extrempositionen hin und her. Wenn sich ein Pendel dagegen beispielsweise in der Atmosphäre befindet, führt der Luftwiderstand (Dämpfung) dazu, dass der maximale Schwingwinkel mit der Zeit kleiner wird und das Pendel schließlich an der Gleichgewichtsposition anhält.
Abbildung
1. Reibungsloser Neutralpunkt
2. Masseloser Stab
3. Massives Pendelgewicht
4. Gleichgewichtsposition
5. Leitkurve des Pendelgewichts
6. Amplitude
Außerdem ändert in einem Schwingzyklus (Periode) das Pendel, wenn es die höchste Position
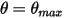
erreicht, die Richtung mit dem Gesamtverlust seiner kinetischen Energie. Bei dem einfachen Schwerkraftpendel wird die kinetische Energie vollständig in die potentielle Energie übertragen, während dann, wenn ein Widerstand des Mediums berücksichtigt wird, ein Teil der kinetischen Energie verloren geht, um die viskose Dämpfung zu überwinden. Die Nettokraft oder die potentielle Energie treibt das Pendel jedoch dazu an, sich in die entgegengesetzte Richtung hin zur Gleichgewichtsposition zu bewegen, wo die kinetische Energie (Geschwindigkeit) maximal und das Potenzial am niedrigsten ist. In diesem Fall gibt

eine No-Bounce-Bedingung für die
Gleichung 2.444, den 1-FG-Drehimpuls, an.
Zusätzlich zur No-Bounce-Bedingung kann ein beweglicher Körper an der Grenzposition möglicherweise keinerlei kinetische Energie verlieren und zurückprallen (perfekte Ablenkung) oder nur einen Teil seiner kinetischen Energie verlieren (partielle Ablenkung). Daher werden die folgenden drei Ablenkungsbedingungen angewendet, wenn die Dynamikgleichungen für Translation (1 FG) und Rotation (1 FG),
Gleichung 2.432 und
Gleichung 2.444 gelöst werden, um die Bewegungen eines Volumenkörpers oder einer Wandberandung für die Strömungsdomäne zu ermitteln:
• No Bounce – Standardmodell in
Creo Flow Analysis. Dadurch wird bestimmt, dass ein Volumenkörper (oder eine Berandung) bei Erreichen seiner Bewegungsgrenze die Richtung ändert und dabei seine kinetische Energie vollständig verloren geht. Wenn
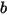
und

Ablenkung und Inzidenz und
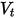
und

die Translations- und Rotationsgeschwindigkeit (nur Betrag) darstellen, wird dieses Ablenkungsmodell wie folgt ausgedrückt:
◦ Translation
Gleichung 2.449
◦ Rotation
Gleichung 2.450
• Partielle Ablenkung – Modell, das vorgibt, dass ein Volumenkörper (oder eine Berandung) bei Erreichen seiner Bewegungsgrenze die Richtung ändert und dabei seine kinetische Energie teilweise verloren geht, wie durch einen benutzerspezifizierten Faktor
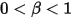
angegeben:
◦ Translation
Gleichung 2.451
◦ Rotation
Gleichung 2.452
• Perfekte Ablenkung – Modell, das vorgibt, dass ein Volumenkörper (oder eine Berandung) bei Erreichen seiner Bewegungsgrenze die Richtung ändert und dabei seine kinetischen Energie in keiner Weise verloren geht,

:
◦ Translation
Gleichung 2.453
◦ Rotation
Gleichung 2.454



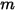 die Masse des sich bewegenden Objekts;
die Masse des sich bewegenden Objekts; 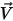 ⃗ ist die lineare/translatorische Geschwindigkeit; und
⃗ ist die lineare/translatorische Geschwindigkeit; und 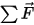 ⃗ sind die Gesamt-/Nettokräfte, die auf den Körper unter der Translation ausgeübt werden. In Gleichung 2.427 ist
⃗ sind die Gesamt-/Nettokräfte, die auf den Körper unter der Translation ausgeübt werden. In Gleichung 2.427 ist 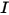 das Trägheitsmoment;
das Trägheitsmoment; 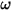 ⃗ ist die Winkelgeschwindigkeit; und
⃗ ist die Winkelgeschwindigkeit; und 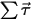 ⃗ ist das Gesamt-/Netto-Drehmoment, das auf den rotierenden Körper wirkt.
⃗ ist das Gesamt-/Netto-Drehmoment, das auf den rotierenden Körper wirkt.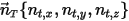 , wird die translatorische Bewegung des Körpers auf einen Freiheitsgrad (1-DOF) reduziert. Anschließend wird Gleichung 2.426 zur linearen Impulserhaltung zu einer skalaren Gleichung entlang der Bewegungsrichtung, da die Bewegungsgeschwindigkeit und -kraft in Bezug auf
, wird die translatorische Bewegung des Körpers auf einen Freiheitsgrad (1-DOF) reduziert. Anschließend wird Gleichung 2.426 zur linearen Impulserhaltung zu einer skalaren Gleichung entlang der Bewegungsrichtung, da die Bewegungsgeschwindigkeit und -kraft in Bezug auf 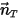 ausgedrückt werden:
ausgedrückt werden: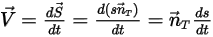

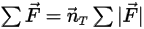
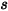 der Betrag des Positionsvektors
der Betrag des Positionsvektors 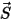 an einem Punkt von Interesse auf dem Volumenkörper entlang der Bewegungsrichtung
an einem Punkt von Interesse auf dem Volumenkörper entlang der Bewegungsrichtung  . In einem kartesischen Koordinatensystem gilt
. In einem kartesischen Koordinatensystem gilt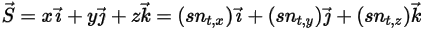

 – Besteht aus Druck- und Schubkräften. Sie werden durch die relative Bewegung zwischen dem Flüssigkeitsfluss und den Flächen des Volumenkörpers verursacht, die in Kontakt mit dem Fluss stehen. Die Druck- und Schubkräfte werden aus den Flow-Lösungen (Ausgabemengen) ermittelt:
– Besteht aus Druck- und Schubkräften. Sie werden durch die relative Bewegung zwischen dem Flüssigkeitsfluss und den Flächen des Volumenkörpers verursacht, die in Kontakt mit dem Fluss stehen. Die Druck- und Schubkräfte werden aus den Flow-Lösungen (Ausgabemengen) ermittelt: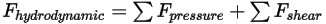
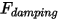 – Eine Verzögerungskraft, die durch die Reibungsdämpfungswirkung verursacht wird. Sie wird durch die Bewegung des Volumenkörperobjekts und den benutzerdefinierten Dämpfungskoeffizienten
– Eine Verzögerungskraft, die durch die Reibungsdämpfungswirkung verursacht wird. Sie wird durch die Bewegung des Volumenkörperobjekts und den benutzerdefinierten Dämpfungskoeffizienten  bestimmt:
bestimmt: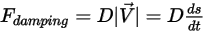
 – Ist abhängig von der Federverschiebung
– Ist abhängig von der Federverschiebung 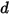 , der Federkonstante
, der Federkonstante 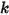 und der Federvorspannkraft
und der Federvorspannkraft 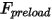 :
: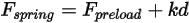
 definiert als:
definiert als: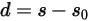
 der Betrag des Positionsvektors
der Betrag des Positionsvektors 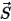 an der vorherigen Position
an der vorherigen Position 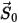 .
.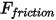 wird modelliert als:
wird modelliert als: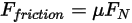
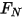 die Normalkomponente der Kontaktkraft, die auf die Körperfläche von Interesse ausgeübt wird. Für den Reibungskoeffizienten
die Normalkomponente der Kontaktkraft, die auf die Körperfläche von Interesse ausgeübt wird. Für den Reibungskoeffizienten 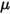 werden der Haftreibungskoeffizient
werden der Haftreibungskoeffizient 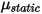 und der Gleitreibungskoeffizient
und der Gleitreibungskoeffizient 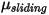 weiter für die stationären bzw. sich bewegenden Körper eingeführt:
weiter für die stationären bzw. sich bewegenden Körper eingeführt:
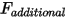 – Für zusätzliche benutzerdefinierte Kräfte hinzugefügt.
– Für zusätzliche benutzerdefinierte Kräfte hinzugefügt.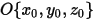 und den Richtungseinheitsvektor
und den Richtungseinheitsvektor  definiert ist, wird die Rotation des Volumenkörpers um die Achse
definiert ist, wird die Rotation des Volumenkörpers um die Achse 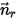 ebenfalls auf eine 1-FG-Rotation reduziert. Entsprechend wird Gleichung 2.427 zur Drehimpulserhaltung ebenfalls zu einer skalaren Gleichung entlang der tangentialen Richtung
ebenfalls auf eine 1-FG-Rotation reduziert. Entsprechend wird Gleichung 2.427 zur Drehimpulserhaltung ebenfalls zu einer skalaren Gleichung entlang der tangentialen Richtung 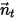 , definiert als:
, definiert als: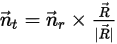
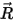 der Vektor, der vom Mittelpunkt der Achse zu einem beliebigen Punkt
der Vektor, der vom Mittelpunkt der Achse zu einem beliebigen Punkt  auf dem Volumenkörper zeigt:
auf dem Volumenkörper zeigt:
 werden umformuliert als:
werden umformuliert als: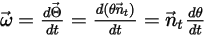
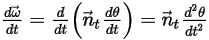
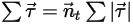
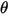 der Rotationswinkel des Punkts
der Rotationswinkel des Punkts 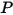 relativ zur Start- oder Referenzposition.
relativ zur Start- oder Referenzposition.
 – Kombination des Drehmoments aufgrund von Druck- und Schubkräften:
– Kombination des Drehmoments aufgrund von Druck- und Schubkräften: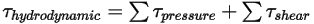
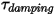 – Hängt von der Rotationsgeschwindigkeit
– Hängt von der Rotationsgeschwindigkeit 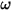 und dem benutzerdefinierten Dämpfungskoeffizienten
und dem benutzerdefinierten Dämpfungskoeffizienten 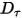 ab:
ab: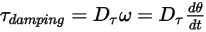
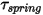 – Drehmoment induziert durch Torsion, die vom Verschiebungswinkel
– Drehmoment induziert durch Torsion, die vom Verschiebungswinkel 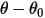 , vom benutzerdefinierten Vorspannungsmoment
, vom benutzerdefinierten Vorspannungsmoment  und von der Torsionskonstante
und von der Torsionskonstante  abhängt.
abhängt.
 der Referenzwinkel. Dieser ist in der Regel die Position der Berandung oder des Volumens während des Modell-Setups, kann jedoch einer anderen Position entsprechen. Bei einer Nullwinkelverschiebung ist der Referenzwinkel
der Referenzwinkel. Dieser ist in der Regel die Position der Berandung oder des Volumens während des Modell-Setups, kann jedoch einer anderen Position entsprechen. Bei einer Nullwinkelverschiebung ist der Referenzwinkel  beispielsweise nicht gleich der Anfangswinkelposition.
beispielsweise nicht gleich der Anfangswinkelposition.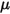 und dem Kontaktmoment aus der Anwendung der Normalkraft
und dem Kontaktmoment aus der Anwendung der Normalkraft 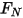 auf die Kontaktfläche:
auf die Kontaktfläche:
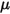 ein benutzerdefinierter Parameter, der in Gleichung 2.438 definiert ist.
ein benutzerdefinierter Parameter, der in Gleichung 2.438 definiert ist.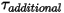 – Für zusätzliche benutzerdefinierte Drehmomente hinzugefügt.
– Für zusätzliche benutzerdefinierte Drehmomente hinzugefügt. freigegeben wird, verursacht die auf seine Masse wirkende Rückstellkraft, dass es um die Gleichgewichtsposition herum schwingt. Der maximale Winkel auf jeder der Seiten der Gleichgewichtsposition
freigegeben wird, verursacht die auf seine Masse wirkende Rückstellkraft, dass es um die Gleichgewichtsposition herum schwingt. Der maximale Winkel auf jeder der Seiten der Gleichgewichtsposition 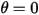 hängt von seiner Freigabeposition
hängt von seiner Freigabeposition  ab. Wenn keine Reibung (reibungsfreier Drehpunkt und Vakuum) vorhanden ist, bleibt der maximale Winkel unverändert, und das Pendel schwingt dauerhaft zwischen denselben Extrempositionen hin und her. Wenn sich ein Pendel dagegen beispielsweise in der Atmosphäre befindet, führt der Luftwiderstand (Dämpfung) dazu, dass der maximale Schwingwinkel mit der Zeit kleiner wird und das Pendel schließlich an der Gleichgewichtsposition anhält.
ab. Wenn keine Reibung (reibungsfreier Drehpunkt und Vakuum) vorhanden ist, bleibt der maximale Winkel unverändert, und das Pendel schwingt dauerhaft zwischen denselben Extrempositionen hin und her. Wenn sich ein Pendel dagegen beispielsweise in der Atmosphäre befindet, führt der Luftwiderstand (Dämpfung) dazu, dass der maximale Schwingwinkel mit der Zeit kleiner wird und das Pendel schließlich an der Gleichgewichtsposition anhält.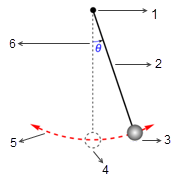
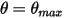 erreicht, die Richtung mit dem Gesamtverlust seiner kinetischen Energie. Bei dem einfachen Schwerkraftpendel wird die kinetische Energie vollständig in die potentielle Energie übertragen, während dann, wenn ein Widerstand des Mediums berücksichtigt wird, ein Teil der kinetischen Energie verloren geht, um die viskose Dämpfung zu überwinden. Die Nettokraft oder die potentielle Energie treibt das Pendel jedoch dazu an, sich in die entgegengesetzte Richtung hin zur Gleichgewichtsposition zu bewegen, wo die kinetische Energie (Geschwindigkeit) maximal und das Potenzial am niedrigsten ist. In diesem Fall gibt
erreicht, die Richtung mit dem Gesamtverlust seiner kinetischen Energie. Bei dem einfachen Schwerkraftpendel wird die kinetische Energie vollständig in die potentielle Energie übertragen, während dann, wenn ein Widerstand des Mediums berücksichtigt wird, ein Teil der kinetischen Energie verloren geht, um die viskose Dämpfung zu überwinden. Die Nettokraft oder die potentielle Energie treibt das Pendel jedoch dazu an, sich in die entgegengesetzte Richtung hin zur Gleichgewichtsposition zu bewegen, wo die kinetische Energie (Geschwindigkeit) maximal und das Potenzial am niedrigsten ist. In diesem Fall gibt  eine No-Bounce-Bedingung für die Gleichung 2.444, den 1-FG-Drehimpuls, an.
eine No-Bounce-Bedingung für die Gleichung 2.444, den 1-FG-Drehimpuls, an.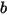 und
und  Ablenkung und Inzidenz und
Ablenkung und Inzidenz und 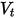 und
und  die Translations- und Rotationsgeschwindigkeit (nur Betrag) darstellen, wird dieses Ablenkungsmodell wie folgt ausgedrückt:
die Translations- und Rotationsgeschwindigkeit (nur Betrag) darstellen, wird dieses Ablenkungsmodell wie folgt ausgedrückt: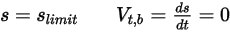
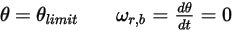
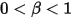 angegeben:
angegeben:
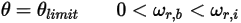
 :
:
