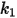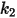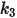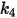粒子沖蝕建模
沖蝕是由於實體粒子在曲面上重複撞擊而導致材料損失的一種現象。沖蝕會損壞管路、閥和其他流體通道。因此,研究沖蝕率及確定流體通道中容易受到沖蝕的區域十分重要。
基於 CFA 的沖蝕建模包括下列步驟:
1. 透過求解納維-斯托克斯方程式可取得流場資料 (如,速度)。
2. 在流場中釋放粒子,並單獨追蹤粒子以獲得撞擊速度與撞擊角度等資訊。
3. 將粒子的撞擊資訊用於沖蝕方程式,可計算撞擊粒子導致的沖蝕比/沖蝕率或表面質量損失。
沖蝕方程式可供研究各種參數對沖蝕的影響,例如:
參考資料:Mazdak Parsi et al. "A comprehensive review of solid particle erosion modeling for oil and gas wells and pipelines applications" (2014)
• 粒子特徵,如大小、形狀、密度、硬度等
• 粒子撞擊資訊,如粒子撞擊速度
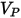
、撞擊角度
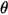
與粒子間相互作用等
• 目標壁內容,如材料密度、硬度等
沖蝕方程式可用來計算沖蝕率
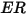
,其定義為 (實體粒子撞擊所致的) 壁材料損失量除以撞擊實體粒子的質量。
Creo Flow Analysis 使用下面部分中所述的沖蝕模型:
參考資料:Mazdak Parsi etc. "CFD simulation of sand particle erosion in gas-dominant multiphase flow" (2015)
Finne 模型
Finne 模型的沖蝕方程式如下所示:
其中,
| 壁材料密度 (kg/m3) |
| 粒子撞擊速度 (m/s) |
| 速度指數 (對於大多數工業應用,等於 2) |
| 維氏硬度 (Pa) |
| 撞擊角度 (度) |
|  此模型會低估粒子撞擊角度大於 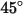 時引起的材料損失程度,並預測法向撞擊不會造成沖蝕。 |
Zhang 模型
Zhang 模型的沖蝕方程式如下所示:
其中,
| 沖蝕比 |
| |
| 壁材料的 Brinell 硬度 (Pa) |
| 粒子形狀係數 |
| 粒子撞擊速度 (m/s) |
| 速度指數 (等於 2.41) |
| 撞擊角度函數 |
對於不同形狀的砂粒,粒子形狀係數
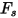
具有下列值:
值 | 砂粒類型 |
1.0 | 尖角或棱角 |
0.53 | 半圓角 |
0.2 | 全圓角 |
撞擊角度函數如下所示:
下表列出
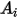
的值:
Oka 模型
Oka 等人的沖蝕方程式如下所示:
方程式 2.406
方程式 2.407
方程式 2.408
方程式 2.409
方程式 2.410
其中,
| 體積沖蝕率 (mm3/kg) |
| 法向撞擊角度下的沖蝕損壞 (mm3/kg) |
| 參照撞擊速度 (m/s) |
| 粒子直徑 (m) |
| 參照粒子直徑 (m) |
| Vicker 硬度 (GPa) |
| | | | | | |
60 | -0.12 | 0.19 | 0.71 | 2.4 | 0.14 | -0.94 |
DNV 模型
DNV 模型的沖蝕方程式如下所示:
其中,
| |
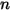 (速度指數) | |
下表列出了
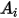
的值:
| | | | | | | |
9.370 | -42.295 | 110.864 | -175.804 | 170.137 | -98.398 | 31.211 | -4.170 |
Mansouri 模型
Mansouri 模型的沖蝕方程式如下所示:
方程式 2.413
方程式 2.414
其中,
| 沖蝕比 |
| 壁材料的 Brinell 硬度 (Pa) |
| 粒子形狀係數 |
| 粒子撞擊速度 (m/s) |
| 速度指數 |
| 撞擊角度函數 |
| Vicker 硬度 (Pa) |
| 撞擊角度 (度) |
下表包含 Mansouri (2015) 沖蝕方程式的
方程式 2.413 與
方程式 2.414 中所使用的不同參數值。
| | | | | |
0.6947 | 2.41 | 0.2 | 0.85 | 0.65 | 4.49e-07 |
Grant-Tabakoff 模型
Grant-Tabakoff 模型的沖蝕方程式如下所示:
方程式 2.415
其中,
方程式 2.416
其中,
| 沖蝕比 |
| 粒子撞擊速度 (m/s) |
| 撞擊角度 (度) |
| 最大沖蝕角度 (度) |
方程式 2.415 中的沖蝕率
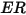
定義為撞擊粒子的每個質量單位 (g) 的材料量 (以 mg 為單位)。速度單位為 ft/s。
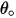
是最大沖蝕角度。例如,對於鋁合金而言,
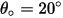
。
Grant-Tabakoff 模型的不同係數值如下表所示:
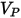 、撞擊角度
、撞擊角度 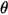 與粒子間相互作用等
與粒子間相互作用等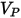 、撞擊角度
、撞擊角度 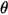 與粒子間相互作用等
與粒子間相互作用等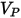 、撞擊角度
、撞擊角度 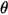 與粒子間相互作用等
與粒子間相互作用等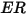 ,其定義為 (實體粒子撞擊所致的) 壁材料損失量除以撞擊實體粒子的質量。
,其定義為 (實體粒子撞擊所致的) 壁材料損失量除以撞擊實體粒子的質量。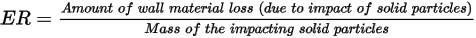
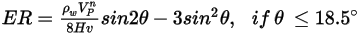
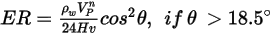
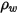
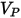
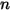
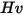
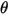
 時引起的材料損失程度,並預測法向撞擊不會造成沖蝕。
時引起的材料損失程度,並預測法向撞擊不會造成沖蝕。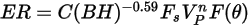
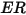
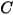
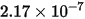
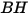
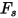
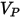
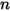
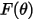
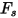 具有下列值:
具有下列值: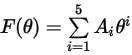
 的值:
的值:
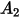
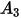
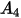
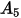
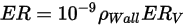
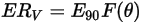
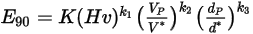
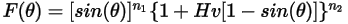
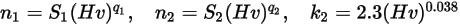
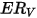
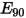
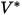
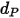
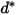
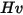
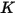
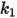
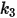
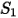
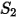
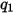
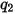
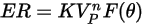
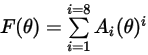
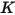
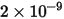
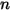 (速度指數)
(速度指數)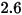
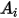 的值:
的值: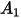
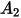
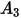
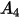
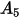
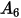
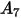
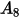
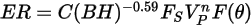
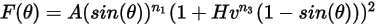
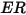
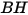
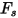
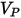
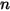
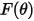
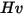
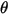
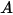
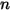
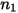
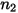
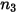
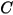
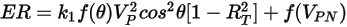
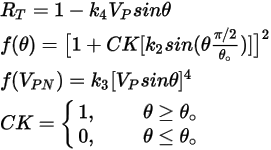
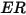
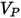
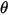
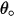
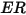 定義為撞擊粒子的每個質量單位 (g) 的材料量 (以 mg 為單位)。速度單位為 ft/s。
定義為撞擊粒子的每個質量單位 (g) 的材料量 (以 mg 為單位)。速度單位為 ft/s。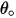 是最大沖蝕角度。例如,對於鋁合金而言,
是最大沖蝕角度。例如,對於鋁合金而言,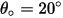 。
。