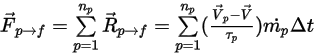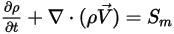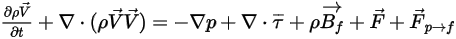離散粒子模型
在離散粒子模型中,可追蹤穿過連續流體相的指定粒子數來建立離散相流動模型。在 Creo Flow Analysis 中,此模型有下列假設與限制:
• 一定數量的球狀粒子穿過連續流體流動相。這些粒子被定義為「有質量」(Has Mass) 或「無質量」(Massless)。
• 釋放位置和時間下的指定半徑決定了粒子的大小,該大小會保持不變。粒子間相互作用可忽略不計。
• 粒子會與流體流和壁邊界相互作用。粒子的體積不會置換任何流體 (粒相的低體積分數) 或干涉幾何 (超大粒子會穿過較小間隙)。
• 連續流體相與粒子之間不會發生熱傳與質傳。假設粒子溫度與流體流的局部溫度相同。
在這些假設下,使用 Lagrangian 方法追蹤每個個別粒子的運動。藉由針對每個粒子形成一組關於時間的常微分方程式 (包含位置與速度方程式) 來執行追蹤。然後,對這些方程式做積分,來計算粒子遍歷流域時的反應。Creo Flow Analysis 中粒子建模方法的特性如下:
• 離散粒子模型遵循歐拉-拉格朗日方法。藉由求解連續性與納維-斯托克斯方程式,可將流體相視為一段連續體。藉由使用拉格朗日方法來追蹤每個個別粒子的運動,可求解離散相。粒子所佔的體積分數並不納入連續相計算中。
• 針對設為「無質量」(Massless) 的粒子,它們會隨流體流移動,或沿流場的流線移動。粒子的大小或半徑並不會影響流體或粒子,而是僅供顯示之用。
• 針對設為「有質量」(Has Mass) 的粒子,其質量由您為指定粒子半徑或直徑所指定的值與粒子密度來決定。作用於粒子的力 (可決定粒子的運動) 包括粒子與流體間的阻力 (慣性力) 與重力。不考量作用於粒子上的紊流分散力。粒子大小會影響粒子與流體間的阻力與後處理。
• 流體相與離散粒相之間動量交換模型的建立方式如下:
◦ 單向耦合 - 僅流體相會影響粒子運動。
◦ 雙向耦合 - 粒子也會透過粒子與流體間的阻力影響流體流。
• 使用粒子壁模型 (例如,粘附反彈、完美反彈與部份反彈) 對壁與粒子間的相互作用進行建模。
• 雖然流體相可以是穩態,也可以是非穩態,但粒子追蹤是一個瞬態過程,在此過程中會牽涉對穿過離散域的粒子路徑做積分。在此方法中,會在不同時間從指定位置釋放或射出個別粒子。從每個粒子的釋放位置開始一直追蹤至目標位置,此目標位置為粒子逸出域的位置或符合特定積分限制的位置。最後,求得全部粒子軌跡的平均值,並將粒子與流體間的相互作用作為流體相動量方程式的源項進行計算。
• 使用「粒子」(Particle) 模組中的相關煙線追蹤方法來顯示粒子的行進路徑。
粒子運動理論
在 Lagrange 方法中,粒子運動由粒子上的力平衡和粒子的釋放條件 (初始條件) 來決定。要對離散粒相進行建模,首先需要根據力平衡建立粒子運動方程式。然後,指定粒子的邊界與初始條件。最後,對粒子運動方程式執行積分,以便實現粒子追蹤。
粒子運動方程式
• 粒子力平衡
對於在連續流體介質中運動行進的離散粒子,粒子的運動由作用於其上的淨力決定。根據牛頓第二定律,可以採用下列拉格朗日形式表示粒子上的力平衡:
方程式 2.366
其中,
| 粒子質量 (kg) |
| 粒子速度 (m/s) |
| 作用於粒子上的淨力 (N),這會影響粒子加速度 |
在卡式座標系中,如果
點 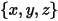 | 粒子的位置 |
| 粒子速度分量 |
使用 Lagrangian 方法時,粒子速度
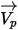
定義為:
方程式 2.367
對於以密度
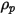
和直徑
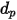
(
Creo Flow Analysis 接受半徑作為輸入) 佔用體積
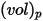
的球狀粒子,按如下方式計算粒子質量
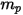
:
方程式 2.368
對於淨力
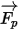
,影響因素包括粒子對流體的阻力、重力效應以及因域旋轉而產生的力 (向心力和科氏力)。其他影響因素是因粒子與流體之間的速度差以及流體受到粒子作用而發生位移時所產生的其他力。在
Creo Flow Analysis 中,
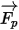
可表示為如下形式:
方程式 2.369
其中,
| 阻力 (N) |
| 重力 (N) |
| 其他力,例如使用者指定的虛擬質量力、壓力梯度力、升力 (n) 等 |
依預設,僅考量作用於粒子的阻力。
方程式 2.370
要封閉
方程式 2.370,需要計算每個個別力產生的作用。
Creo Flow Analysis 中採用的子模型或公式如下:
◦ 施加於粒子的阻力
作用於粒子上的氣動阻力與相滑移速度 (流體與粒子之間的速度差) 成正比。假設粒子在指定時間內與粒子處在同一空間中,流體的流動速度等於
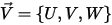
,則阻力可表示為:
方程式 2.371
其中,
對於直徑為
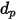
的球狀粒子,
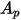
是最大的橫截面面積:
方程式 2.372
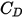
是阻力係數,取決於相對雷諾數
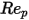
:
方程式 2.373
其中,
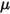
是流體動態黏度 (Pa-s)。
引入阻力係數
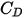
可解釋實心球體之黏性阻力的實驗結果。利用各種模型或經驗相關運算來決定阻力函數
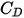
(
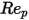
),進而估計流體與粒子間的交換量。對於光滑球狀粒子,在多個模型中,最完整的
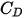
函數是由 Morsi 與 Alexander 修正得到,
參考資料:S. A. Morsi and A. J. Alexander, "An Investigation of Particle Trajectories in Two-Phase Flow Systems", J. Fluid Mech., 55(2) 193–208, September 26 1972.
其通式為:
方程式 2.374
其中,
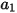
、
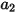
與
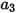
是模型常數,其值取決於相對雷諾數,如下表所示:
| | | |
0 < 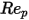 <=0.1 | 0 | 24 | 0 |
0.1 < 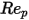 <=1 | 3.690 | 22.73 | 0.0903 |
1< 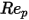 <=10 | 1.222 | 29.1667 | -3.8889 |
10 < 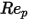 <=100 | 0.6167 | 46.50 | -116.67 |
100 < 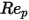 <=1000 | 0.3644 | 98.33 | -2778 |
1000 < 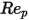 <=5000 | 0.357 | 148.62 | -47500 |
5000 < 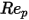 <=10000 | 0.46 | -490.546 | 578700 |
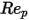 >10000 | 0.5191 | -1662.5 | 5416700 |
該表格顯示,當粒子雷諾數 (黏性流況) 非常低時,即
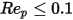
,流經球狀粒子的流動阻力係數仍符合史脫克斯定律:
方程式 2.375
相反地,當
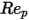
足夠大,以致慣性效應超過黏性效應時,流體與粒子間的流動處於慣性流況或牛頓流況。從此表格中,可以發現阻力係數對相對雷諾數的依存性變低。此外,通常會使用
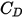
的常數值,而不是完整的 Morsi 和 Alexander 模型:
方程式 2.376
在黏性流況和慣性流況之間的過渡區域 (
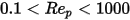
) 中,黏性效應和慣性效應二者對於球狀粒子都很重要。因此,阻力係數是關於相對雷諾數的复變函數,可透過 Morsi 與 Alexander 模型或其他相關運算進行估算。例如,根據 Schiller 與 Naumann 模型:
參考資料:L. Schiller and Z. Naumann, "Z. Ver. Deutsch. Ing. 77. 318. 1935.
方程式 2.377
方程式 2.378
方程式 2.379
因此,預設的 (僅考量阻力) 粒子力平衡方程式為:
方程式 2.380
• 包含重力項
依預設,粒子力平衡方程式中不包含重力項。可以在
Creo Flow Analysis 中啟用重力項。對於浸入流體流中的粒子,因重力效應而產生的浮力等於粒子所置換之流體的重量。假設
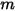
是粒子所置換之流體的質量,而
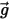
是重力向量,則由此產生的力如下:
方程式 2.381
或將每單位粒子質量的力指定為:
方程式 2.382
力平衡方程式的形式如下:
方程式 2.383
• 施加於粒子的旋轉力
對於旋轉座標系中的流體流動模型,旋轉引起的其他力項
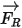
是粒子加速度固有的一部份。它由科氏力與向心力效應構成:
方程式 2.384
或將每單位粒子質量的旋轉力指定為:
方程式 2.385
其中,
新增此力項之後,粒子平衡方程式變為:
方程式 2.386
當在旋轉座標系中求解流動時,
方程式 2.386 用於控制粒子在 Lagrange 系統中的運動。
粒子的邊界與初始條件
在 Lagrange 方法中,粒子追蹤是一個瞬態過程。因此,需要邊界與初始條件才能計算粒子的軌跡。邊界條件用於定義粒子在計算域邊界處的反應,特別是粒子與壁之間的相互作用。初始條件可決定粒子在邊界處的釋放情況,包括釋放位置、頻率、速度、粒子類型和大小 (半徑),以及粒子數。
邊界條件
Creo Flow Analysis 提供離散相邊界條件,用以確定粒子在邊界處的反應。當粒子到達流域邊界 (包括物理邊界和固體與流體間的介面) 時,例如壁或入口邊界,會發生下列其中一種情況:
• 粒子透過彈性或非彈性碰撞發生反射。
• 粒子透過邊界逸出,因此不納入邊界撞擊點的計算中。
• 粒子被壁面俘獲,因此不納入邊界撞擊點的計算中。
• 粒子穿過內部邊界區域,例如,風扇或多孔跳躍。
• 粒子與邊界間的相互作用由使用者定義的方法來決定,以針對粒子撞擊邊界時的粒子反應進行建模。
根據邊界處的粒子反應,將流邊界條件與介面重新編組為三種類型的離散粒子邊界條件:開放、對稱與壁。
• 開放離散粒子邊界
粒子或流線可以流出計算域。開放邊界是尤拉系統中流體流相的入口或出口邊界。它也可套用至諸如壁與對稱等流動邊界。在開放粒子邊界處,粒子會根據粒子速度方向流出或進入域。
假設
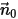
為指向計算域外部之開放邊界的單位法向量,且粒子邊界速度為
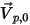
。如果
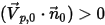
,則速度向量
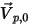
指向計算域外部。這表示粒子穿過邊界逸出,因此不納入邊界撞擊點的計算中。
• 對稱粒子邊界
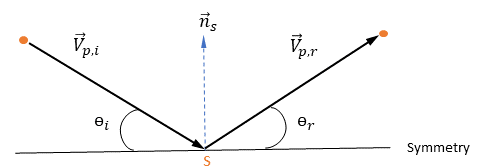
當計算域中的粒子或煙線撞擊離散對稱邊界時,邊界條件會將其反射回域中。對於離散粒相,對稱粒子邊界通常與尤拉系統中的流動對稱相對應。它也可以是粒子的釋放位置。
假設
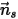
是對稱在點
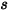
處的法向對稱單位向量,其方向背離對稱,指向計算域外部。引入
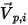
與
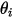
,用以表示粒子對稱邊界處的粒子撞擊速度角,如下圖所示。當粒子發生對稱反射時,其總動能守恆:切向速度保持不變,而法向速度分量僅變更符號。粒子對稱邊界條件可表示為:
方程式 2.387
其中,
| 點 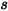 處的角度:對稱 (度) |
| 粒子入射速度的量值 (m/s) |
| 粒子反射速度的量值 (m/s) |
• 壁粒子邊界
對於液滴,液滴與壁之間的相互作用取決於壁溫、壁材料和粗糙度、撞擊角度與撞擊速度、是否存在壁膜,以及各種其他參數。因此,使用一系列子模型來再現壁與粒子間相互作用的不同流況,並解釋流動參數與壁邊界條件的影響。
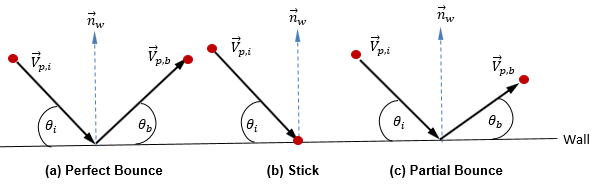
在目前的離散粒子模型中,假設粒子的形狀、大小和質量保持不變。此外,還應該考量流體與粒子處於熱平衡。因此,用一種簡單的方法來描述 (有質量) 粒子與壁的碰撞過程:在此碰撞過程中,粒子僅與壁交換動量,而粒子與壁的相互作用可以三種方式進行。這三種方式是完美反彈、粘附反彈與部份反彈。
◦ 完美反彈 - 粒子或煙線在撞擊壁時發生反射。粒子的動量與動能完全守恆。入射角等於反射角,而壁法向速度分量會變更符號:
方程式 2.388
其中,
| 壁法向單位向量 |
| 壁邊界處的角度 (度) |
| 粒子入射速度的量值 (m/s) |
| 粒子反彈速度的量值 (m/s) |
◦ 粘附 - 粒子與壁碰撞,失去其所有動量與能量,進而粘附於壁上:
如果不考量粒子沿壁累積,則粒子將完全不納入邊界撞擊點的計算中。
◦ 部份反彈 - 介於完美反彈與粘附反彈之間的壁粒子條件。粒子或煙線雖然在壁處發生反彈,但還是會在法向和/或切向方向上損失一部份能量。粒子的動量與動能不守恆,且入射角通常大於反射角:
透過粒子與壁間的相互作用而損失的能量由使用者輸入來指定:
▪ 法向能量損失 - 指定粒子在壁上損失之動能的法向分量。
▪ 切向能量損失 - 指定粒子在壁上損失之動能的切向分量。
在
Creo Flow Analysis 中,是粒子反彈還是粘附由指定的最大和最小法向速度值來決定。假設
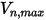
是指定的粒子最大法向速度,而
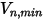
是指定的粒子最小法向速度,且具有以下條件:
▪ 如果
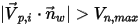
或
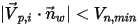
,則粒子會在壁處發生反彈。
▪ 如果
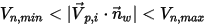
,則粒子會粘附於壁上。
粒子與壁間的相互作用模型僅適用於設為「有質量」(Has mass) 的粒子。無質量的粒子會沿壁跟隨流線移動。
請注意,粒子壁邊界可以是外壁和流固介面。如同開放與對稱粒子邊界一樣,可以從壁邊界釋放粒子。
初始條件 (釋放粒子)
初始條件為所有用於描述個別粒子瞬時條件的離散相因變數提供起始值。對於 Lagrange 系統粒子追蹤,用於確定初始條件的程序包括從邊界 (開放、對稱、壁和介面) 釋放粒子 (頻率及分佈),以及為每個粒子指派屬性。
當啟用「釋放粒子」(Release Particle) 時,下列參數或變數是粒子運動的初始條件:
對粒子運動方程式做積分
要追蹤粒子運動,需要在 Lagrange 系統中對每個粒子的軌跡方程式進行解析求解或數值求解 (積分)。根據
方程式 2.367 和
方程式 2.386,運動方程式改寫如下:
方程式 2.391
方程式 2.392
其中,
| 粒子的位置向量 |
| 包括加速度,因阻力以外的其他所有力 (如重力、旋轉效應等) 而導致 |
方程式 2.391 和
方程式 2.392 是一組耦合的常微分方程式。根據給定的初始條件與邊界條件,對時間步長
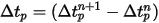
內的粒子速度進行正向歐拉積分,以計算粒子位移 (
方程式 2.391):
方程式 2.393
其中,
在第一個時間步長處,
其中,
方程式 2.394
在此正向積分方法中,假設在時間步驟步長起點計算的粒子速度在整個步長內最大。在時間步長終點,藉由求解粒子動量
方程式 2.392 來計算新的粒子速度。假設
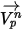
、
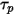
與
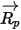
在時間段
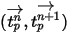
內為常數,且流體屬性取自時間步長起點時間
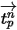
,則
方程式 2.392 的解析解為:
方程式 2.395
要計算
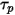
與
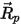
,需要用到粒子所在位置處的密度、黏度與速度等流體變數。將它們視為粒子目前所在流體流相的單元值。此解析法雖然有效,但對於較大時間步長以及粒子與連續流體不處於流體動力平衡的情況,該法可能會變得不太準確。在這種情況下,使用數值法對
方程式 2.392 做積分。
粒子-流體耦合
在 Euler-Lagrange 方法中,假設連續流體流透過力、熱及質量傳遞影響粒子反應。例如,粒子力平衡
方程式 2.370 中的力項
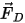
與流體對粒子的氣動阻力有關。粒相雖然被視為離散相且不會以體積形式置換流體,但粒子可以透過動量交換也有可能是質量和熱交換對流體產生反作用。粒子對流的影響稱為粒子-流體耦合。這種耦合分為兩個類別:
• 單向耦合
單向耦合允許流體影響粒子的軌跡,但粒子不會對流體產生任何影響。對於無質量的粒子,粒子與流體間的相互作用是單向耦合: 粒子會隨著流體流移動。對於有質量的粒子,單向耦合可以是具有低離散相負載之流體可接受的近似結果,其中粒子對流體流的影響可忽略不計。
對於連續流體相,按不存在離散粒相的單相流體計算流場。然後,根據計算出的流場與初始條件來追蹤粒子運動。對於穩態流,藉由求解連續性與納維耶何-史托克斯方程式取得連續相流的收斂解之後,進行粒子追蹤。對於瞬態流模擬,系統會在流模擬的每個時間步長終點追蹤粒子運動。
• 雙向耦合
對於有質量的粒子,雙向耦合允許流體影響粒子的軌跡。它也會考量粒子對連續流體相的影響。在不考量質量和熱傳遞的情況下,流體與粒子間的雙向相互作用僅與動量交換有關。藉由追蹤每個個別粒子穿過控制體積時取得或失去的動量來計算從連續相傳遞到離散相的動量。在雙向耦合中,需要將粒子與流體間的動量交換納入流體動量方程式中,才能解釋離散相軌跡對連續體的影響。在
方程式 2.386 中,僅阻力可以解釋粒子與流體間的動量交換,因此將其納入動量方程式中。請注意,對於無質量的粒子,不會計算流體與粒子間的互換項,因此,離散相軌跡不會影響連續體。
要將粒子與流體間的阻力效應納入連續相動量方程式中,需將穿過流體之每個粒子的阻力套用至此時間步長內粒子所在的控制體積塊中。對於粒子
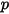
,根據以下微分方程式計算因阻力
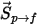
產生的動量源:
方程式 2.396
連續相的粒子源是與該粒子的數值流速 (質量流速除以粒子質量) 相乘的源項
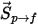
:
方程式 2.397
其中,
假設
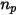
是在時間步長
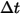
處穿過控制體積塊的粒子數,則粒子與流體間的總源項為:
方程式 2.398
納入流體與粒子間的阻力之後,針對連續相求解的控制方程式現表示為:
方程式 2.399
方程式 2.400
對於單向耦合,
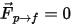
連續流體相由精確的單一相連續性和動量方程式控制。對於雙向耦合,其中包含附加的粒子與流體間阻力源項。
方程式 2.399 和
方程式 2.400 的求解方法與單相流的求解方法相同。
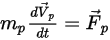
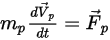
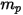
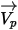
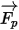
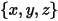
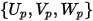
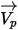 定義為:
定義為: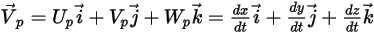
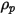 和直徑
和直徑 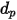 (Creo Flow Analysis 接受半徑作為輸入) 佔用體積
(Creo Flow Analysis 接受半徑作為輸入) 佔用體積 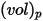 的球狀粒子,按如下方式計算粒子質量
的球狀粒子,按如下方式計算粒子質量 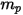 :
: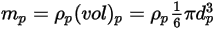
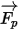 ,影響因素包括粒子對流體的阻力、重力效應以及因域旋轉而產生的力 (向心力和科氏力)。其他影響因素是因粒子與流體之間的速度差以及流體受到粒子作用而發生位移時所產生的其他力。在 Creo Flow Analysis 中,
,影響因素包括粒子對流體的阻力、重力效應以及因域旋轉而產生的力 (向心力和科氏力)。其他影響因素是因粒子與流體之間的速度差以及流體受到粒子作用而發生位移時所產生的其他力。在 Creo Flow Analysis 中,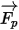 可表示為如下形式:
可表示為如下形式: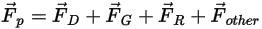
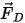
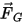
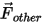
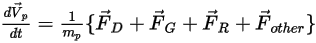
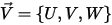 ,則阻力可表示為:
,則阻力可表示為: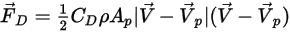
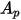
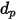 的球狀粒子,
的球狀粒子,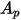 是最大的橫截面面積:
是最大的橫截面面積: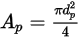
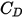 是阻力係數,取決於相對雷諾數
是阻力係數,取決於相對雷諾數 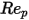 :
: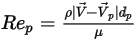
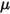 是流體動態黏度 (Pa-s)。
是流體動態黏度 (Pa-s)。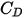 可解釋實心球體之黏性阻力的實驗結果。利用各種模型或經驗相關運算來決定阻力函數
可解釋實心球體之黏性阻力的實驗結果。利用各種模型或經驗相關運算來決定阻力函數 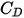 (
(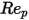 ),進而估計流體與粒子間的交換量。對於光滑球狀粒子,在多個模型中,最完整的
),進而估計流體與粒子間的交換量。對於光滑球狀粒子,在多個模型中,最完整的 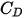 函數是由 Morsi 與 Alexander 修正得到,
函數是由 Morsi 與 Alexander 修正得到,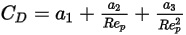
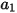 、
、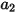 與
與 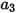 是模型常數,其值取決於相對雷諾數,如下表所示:
是模型常數,其值取決於相對雷諾數,如下表所示: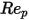
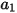
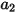
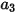
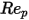 <=0.1
<=0.1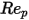 <=1
<=1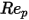 <=10
<=10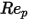 <=100
<=100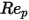 <=1000
<=1000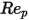 <=5000
<=5000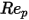 <=10000
<=10000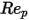 >10000
>10000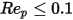 ,流經球狀粒子的流動阻力係數仍符合史脫克斯定律:
,流經球狀粒子的流動阻力係數仍符合史脫克斯定律:
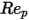 足夠大,以致慣性效應超過黏性效應時,流體與粒子間的流動處於慣性流況或牛頓流況。從此表格中,可以發現阻力係數對相對雷諾數的依存性變低。此外,通常會使用
足夠大,以致慣性效應超過黏性效應時,流體與粒子間的流動處於慣性流況或牛頓流況。從此表格中,可以發現阻力係數對相對雷諾數的依存性變低。此外,通常會使用 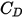 的常數值,而不是完整的 Morsi 和 Alexander 模型:
的常數值,而不是完整的 Morsi 和 Alexander 模型: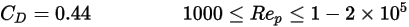
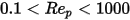 ) 中,黏性效應和慣性效應二者對於球狀粒子都很重要。因此,阻力係數是關於相對雷諾數的复變函數,可透過 Morsi 與 Alexander 模型或其他相關運算進行估算。例如,根據 Schiller 與 Naumann 模型:
) 中,黏性效應和慣性效應二者對於球狀粒子都很重要。因此,阻力係數是關於相對雷諾數的复變函數,可透過 Morsi 與 Alexander 模型或其他相關運算進行估算。例如,根據 Schiller 與 Naumann 模型: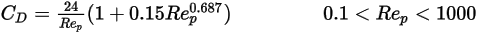
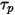 :
: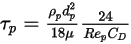
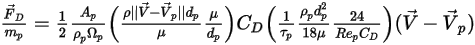
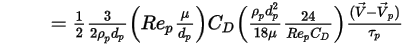
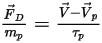
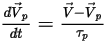
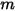 是粒子所置換之流體的質量,而
是粒子所置換之流體的質量,而 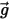 是重力向量,則由此產生的力如下:
是重力向量,則由此產生的力如下: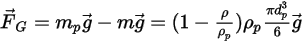
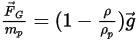
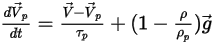
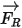 是粒子加速度固有的一部份。它由科氏力與向心力效應構成:
是粒子加速度固有的一部份。它由科氏力與向心力效應構成: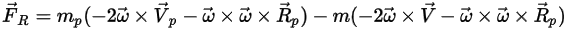
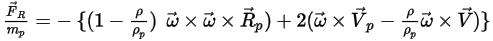
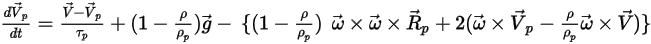
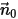 為指向計算域外部之開放邊界的單位法向量,且粒子邊界速度為
為指向計算域外部之開放邊界的單位法向量,且粒子邊界速度為 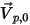 。如果
。如果 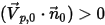 ,則速度向量
,則速度向量 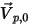 指向計算域外部。這表示粒子穿過邊界逸出,因此不納入邊界撞擊點的計算中。
指向計算域外部。這表示粒子穿過邊界逸出,因此不納入邊界撞擊點的計算中。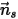 是對稱在點
是對稱在點 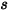 處的法向對稱單位向量,其方向背離對稱,指向計算域外部。引入
處的法向對稱單位向量,其方向背離對稱,指向計算域外部。引入 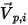 與
與 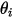 ,用以表示粒子對稱邊界處的粒子撞擊速度角,如下圖所示。當粒子發生對稱反射時,其總動能守恆:切向速度保持不變,而法向速度分量僅變更符號。粒子對稱邊界條件可表示為:
,用以表示粒子對稱邊界處的粒子撞擊速度角,如下圖所示。當粒子發生對稱反射時,其總動能守恆:切向速度保持不變,而法向速度分量僅變更符號。粒子對稱邊界條件可表示為: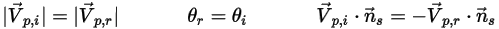
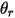
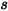 處的角度:對稱 (度)
處的角度:對稱 (度)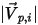
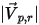
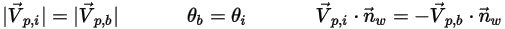
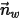
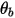
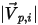
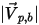
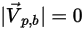
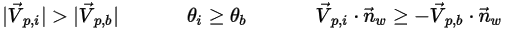
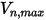 是指定的粒子最大法向速度,而
是指定的粒子最大法向速度,而 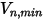 是指定的粒子最小法向速度,且具有以下條件:
是指定的粒子最小法向速度,且具有以下條件: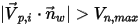 或
或 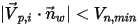 ,則粒子會在壁處發生反彈。
,則粒子會在壁處發生反彈。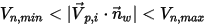 ,則粒子會粘附於壁上。
,則粒子會粘附於壁上。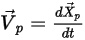
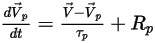
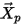
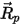
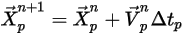
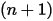
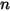
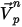
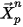
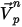

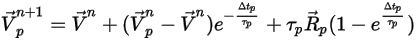
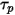 與
與 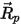 ,需要用到粒子所在位置處的密度、黏度與速度等流體變數。將它們視為粒子目前所在流體流相的單元值。此解析法雖然有效,但對於較大時間步長以及粒子與連續流體不處於流體動力平衡的情況,該法可能會變得不太準確。在這種情況下,使用數值法對方程式 2.392 做積分。
,需要用到粒子所在位置處的密度、黏度與速度等流體變數。將它們視為粒子目前所在流體流相的單元值。此解析法雖然有效,但對於較大時間步長以及粒子與連續流體不處於流體動力平衡的情況,該法可能會變得不太準確。在這種情況下,使用數值法對方程式 2.392 做積分。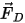 與流體對粒子的氣動阻力有關。粒相雖然被視為離散相且不會以體積形式置換流體,但粒子可以透過動量交換也有可能是質量和熱交換對流體產生反作用。粒子對流的影響稱為粒子-流體耦合。這種耦合分為兩個類別:
與流體對粒子的氣動阻力有關。粒相雖然被視為離散相且不會以體積形式置換流體,但粒子可以透過動量交換也有可能是質量和熱交換對流體產生反作用。粒子對流的影響稱為粒子-流體耦合。這種耦合分為兩個類別: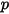 ,根據以下微分方程式計算因阻力
,根據以下微分方程式計算因阻力 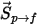 產生的動量源:
產生的動量源: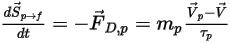
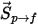 :
: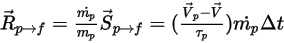
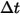
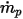
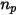 是在時間步長
是在時間步長 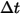 處穿過控制體積塊的粒子數,則粒子與流體間的總源項為:
處穿過控制體積塊的粒子數,則粒子與流體間的總源項為: