辐射传热建模
在热流体系统中,固体表面和/或流体流会因辐射而受到加热或冷却。在 CFA 模型中,通过求解辐射传输方程 (RTE),然后求出总能量守恒方程的辐射源项,以此解释辐射传热。Creo Flow Analysis 中选择了一种广泛使用的建模方法,即表面对表面 (S2S) 辐射模型。
辐射传输方程
当辐射光线以特定方向穿透吸收、发射和散射介质层时,光线会在与其背离的方向上发生吸收和散射现象而损失能量。光线还会在朝向其的方向上发生发射和散射现象而从介质中的光源获得能量。如果光线在无限介质层上的总能量平衡,即会得到一个微分方程,称为辐射传输方程 (RTE)。
为了推导出辐射传输方程,可以考虑强度为
I 的入射辐射光线穿过一介质 (例如气体),在
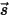
方向上的增量厚度为 ds,如
图所示。穿过介质层后,位置
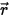
⃗ 和方向
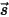
上的入射光线有四种变化方式,其作用在于增强 (能量获得 +) 或减弱 (能量损失 -) 辐射强度
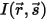
:
• 吸收 - 一种介质 (例如气体) 会吸收穿过其中的一部分辐射能量。如果吸收系数为
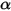
,则通过吸收损失的辐射能量为:
方程 2.282
• 散射 - 当光线穿过介质 (例如气体) 时,介质会将一部分辐射能量散射到另一方向 (背离方向
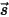
)。如果散射系数为
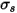
,则通过散射损失的辐射能量为:
方程 2.283
• 发射 - 介质会作为灰体,根据其局部温度 (
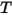
) 和光线的发射特性来发射光线的辐射能量。根据斯特藩-玻尔兹曼定律和发射与吸收之间的互易性 (
方程 2.274 和
方程 2.279),由介质发射出的辐射率为:
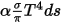
此外,假设 n 是介质的折射率 (定义为光在真空中的速度与其在指定介质中的速度之比),则通过辐射光线获得的实际能量为:
方程 2.284
• 其他辐射源的散射 - 介质层中其他辐射源的一小部分会被散射为辐射光线,具体需视位置和方向矢量
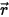
和
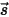
而定。引入
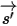
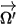
来表示辐射束的方向和立体角,以及引入
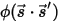
来表示相位函数之后,各个方向上传播的光线散射到
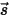
⃗ 方向的强度分量如下:
方程 2.285
如果入射辐射强度为
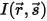
,而出射辐射强度为
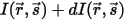
,则
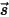
⃗ 方向上的辐射能量平衡具有如下形式:
方程 2.286
方程 2.287
RTE 是表示固定方向
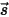
上辐射强度
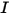
的一阶积分微分方程。要在域中求解此方程,需要给出域中的温度场,同时还需要给出内部和外部表面上
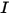
的边界条件,以及两种不同介质之间的界面。
通过求解总能量 (包括辐射源) 守恒方程可得到局部介质温度 (如
热模块中所述)。但是,对于热辐射,边界处理则较为复杂,具体需视辐射模型而定。边界通常可以是发射、反射和吸收能量的不透明介质,也可以是同时透射能量的半透明介质。反射和透射可以是漫反射和/或镜面反射。例如,在发生灰体辐射的发射和反射不透明边界上,根据反射类型,光线强度可表示为如下形式:
◦ 发生漫辐射和反射的不透明边界:
方程 2.288
◦ 发生漫辐射和镜面反射的不透明边界:
方程 2.289
其中,
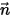 ⃗ | 位置 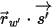 处表面的单位法向矢量 |
| 漫反射光线的方向和立体角 (在各个方向上均匀反射) |
| 镜面反射光线的方向 (理想反射取决于入射方向) |
| 表面反射率、漫反射率和镜面反射率分别具有以下关系: 方程 2.290 |
对于给定的边界条件,
方程 2.287 用于控制辐射强度在指定方向上的传输。对于灰体辐射,应在球面内的各个不同方向上对
方程 2.287 进行求解。对于非灰辐射,其强度还与波长有关。因此,需要在整个波段范围内的各个方向上对其进行求解。很显然,直接求解辐射传输方程会非常耗时。因此,在许多工程模拟中,最好使用近似简化的模型来解释方向和光谱的相关性。在 CFD 仿真中,通常采用下列辐射模型,详细说明可在下列参考资料中找到。
参考资料:R. Siegel and J. R. Howell, "Thermal Radiation Heat Transfer", Hemisphere Publishing Corporation, Washington DC, 1992.
▪ 罗斯兰德辐射模型
参考资料:R, Siegel and J. R. Howell, "Thermal Radiation Heat Transfer", Hemisphere Publishing Corporation, Washington DC, 1992.
▪ P-1 辐射模型
参考资料:R. Siegel and J. R. Howell, Thermal Radiation Heat Transfer, Hemisphere Publishing Corporation, Washington DC, 1992.
▪ 离散传递辐射模型
参考资料:N. G. Shah, "A New Method of Computation of Radiant Heat Transfer in Combustion Chambers", PhD thesis, Imperial College of Science and Technology, London, England, 1979.
参考资料:M. G. Carvalho, T. Farias, and P. Fontes, "Predicting Radiative Heat Transfer in Absorbing, Emitting, and Scattering Media Using the Discrete Transfer Method", In W. A. Fiveland et al., editor, Fundamentals of Radiation Heat Transfer, volume 160, pages 17-26. ASME HTD, 1991.
▪ 表面对表面 (S2S) 辐射模型
参考资料:R. Siegel and J. R. Howell, "Thermal Radiation Heat Transfer", Hemisphere Publishing Corporation, Washington DC, 1992.
▪ 离散坐标 (DO) 辐射模型
参考资料:G. D. Raithby and E. H. Chui, A Finite-Volume Method for Predicting a Radiant Heat Transfer in Enclosures with Participating Media”, J. Heat Transfer, 112:415-423, 1990.
参考资料:E. H. Chui and G. D. Raithby, Computation of Radiant Heat Transfer on a Non-Orthogonal Mesh Using the Finite-Volume Method”, Numerical Heat Transfer, Part B, 23:269-288, 1993.
每个模型在精度和成本方面都有其自身的优势和局限。例如,虽然罗斯兰德模型无法求解入射辐射的传输方程,但该模型是运行速度最快的辐射模型,且所需的额外内存最少。罗斯兰德因其对辐射传输方程的过度简化,只能用于具有光学厚度 (光学厚度是介质中入射辐射功率与透射辐射功率之比的自然对数) 的介质。
离散坐标 (DO) 辐射模型会将
方程 2.287 转换为以空间坐标
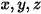
表示的辐射强度传输方程,并针对与矢量方向
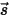
关联的有限个离散立体角进行求解。所选的立体角数量直接决定了精度和计算成本。DO 建模方法也与流体流和能量方程所使用的方法相同。目前,该模型是涵盖整个光学厚度范围的最为常见的一种辐射模型,适合解决从表面对表面辐射到介质参与辐射 (如燃烧系统) 等问题。但是,对于非灰辐射,DO 模型的计算成本很高。
在上述辐射模型中,表面对表面 (S2S) 辐射模型尤其适用于在不考虑参与介质的情况下对封闭体辐射传输进行建模。典型示例有辐射空间加热器和汽车发动机舱与车身底部系统。在这些情况下,介质参与辐射的辐射模型有时不奏效。尽管角系数计算本身可能会占用大量 CPU,但与 DO 辐射模型相比,S2S 模型每次迭代所需的时间更短,执行速度更快。在 Creo Flow Analysis 中,当前选择的辐射传热模型是 S2S 辐射模型。
表面对表面 (S2S) 辐射模型
表面对表面辐射模型解释了在没有参与介质的情况下漫灰表面所构成的封闭体中的辐射能量交换。表面对表面辐射能量交换取决于两个主要因素:所涉及表面的辐射特性,以及包括表面面积和形状,及与其他位置的的相对位置 (分离距离和方向) 在内的几何参数。在 S2S 辐射模型中,表面辐射传热被视为漫灰辐射模型,而几何参数则由称为角系数的几何函数予以解释。
• 漫灰辐射
S2S 辐射模型假设表面为灰体,且具有漫反射特性 (灰体辐射)。对于灰体表面,表面的发射率
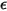
和吸收率
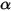
均与出射光线和入射光线的波长无关。根据基尔霍夫热辐射定律 (
方程 2.274),发射率等于吸收率:
方程 2.291
此外,假设一个漫射表面,该表面上不会发生镜面反射,并且此表面上入射辐射的反射率 (
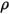
) 相对于立体角各向同性。根据
方程 2.290,表面反射率的计算方式如下:
方程 2.292
其中,
对于透明或半透明表面,透射率
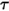
同样与波长无关:
方程 2.293
漫灰表面对表面模型假设表面之间的辐射能量交换几乎不受分隔介质的影响。因此,如果将一定量的辐射能量
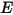
入射到每单位面积的表面上 (辐照度),则反射、吸收和透射的辐射能量分量分别为
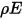
、
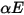
和
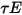
。对于大多数应用而言,表面对红外光谱中的热辐射不透明,因此,可进一步将辐射表面视为不透明表面。因此,可忽略透射率,即
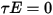
。根据
方程 2.273 和
方程 2.274,表面反射率
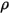
可表示为:
方程 2.294
假设存在表面漫灰辐射,将基于每个表面上的能量守恒来构造 S2S 建模方程。
• S2S 建模方程
S2S 模型的主要假设是在封闭系统中,辐射传热仅发生在漫灰表面之间 (灰体辐射)。可以忽略用于分隔表面的介质中的辐射吸收、发射或散射。因此,对于数值分析,仅需考虑表面对表面辐射。
离开给定表面的辐射能通量由直接发射和反射的能量构成。反射的能通量取决于来自外界的入射能通量,可以用离开其他所有表面的能通量来表示。要计算表面的净辐射能流,为便于计算,可以定义辐射度
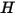
,即每单位面积的发射功率 (发射率)
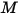
和表面每单位面积所接收的辐射功率的反射分量 (辐照度)
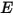
之和:
方程 2.295
对于不透明表面 (
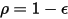
),辐射度为:
方程 2.296
因此,根据 S2S 模型中的假设,可构建下列线性方程组来计算封闭系统中每个表面上的辐射度。假设
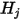
表示任意表面
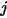
的辐射度,
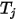
是表面温度,而
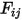
是表面
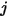
和

之间的角系数,则表面

的辐射度为:
方程 2.297
其中
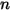
是参与辐射传热的表面数量。引入克罗内克符号
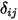
并对灰体辐射应用斯特藩-玻尔兹曼定律 (
方程 2.278) 之后,可重新整理
方程 2.297 并推导出 S2S 建模方程:
方程 2.298
使用预先计算的角系数
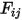
求解
方程 2.298 的线性方程组,可得出参与表面的
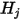
。然后,便可轻松计算出每个表面上的净辐射热流。对于表面

,净辐射热通量
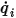
即每单位面积出射 (
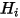
) 与入射 (
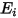
) 辐射的差值。根据
方程 2.278 和
方程 2.296,可以推导出下列通量公式:
方程 2.299
对于给定的表面面积
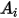
,离开表面的净辐射热流
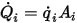
的计算公式为:
方程 2.300
S2S 模型由
方程 2.298 形式的线性方程组构成。应用该模型的优点在于,对于给定的角系数和温度,可通过求解线性方程组来计算净热流,且通过应用数值算法即可完成计算。但是,应用建议的表面对表面模型,其主要难点在于计算 n 个参与表面的
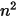
个角系数。此过程非常耗时,特别是表面数量越多,计算越耗时。
计算角系数
在 S2S 建模
方程 2.298 中,角系数
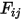
是指离开表面

和撞击表面
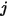
的辐射占比。如
图 2.37 所示,假设
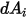
是表面

的微分面积,
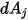
是表面
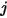
的微分面积,而
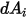
和
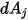
之间的距离是
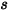
,则在距离
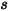
范围内,从
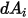
至
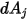
的角系数
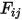
的表达如下所示:
方程 2.301
其中
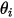
和
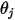
分别是两个微分面积上表面法向与光线之间的夹角。
图 2.37
如果
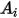
和
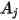
分别是表面

和
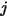
的给定面积,则表面

到表面
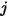
的角系数即
方程 2.301 对表面

和
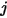
的平均面积积分:
方程 2.302
请注意,仅当两个表面彼此可见,或角系数为非零时,才会发生表面对表面辐射。引入克罗内克符号
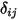
来表示
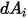
和
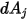
之间的可见性:
方程 2.303
方程 2.304
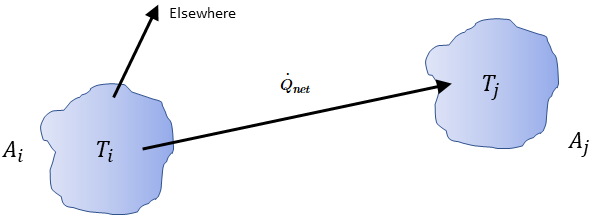
对于任何两个彼此可见的表面,给定表面

仅会将部分出射辐射能量辐射到表面
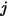
,如
图 2.378 所示。因此,无量纲角系数
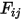
用于表示离开表面

与到达表面
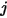
的能量占比。这些特征显示在以下列表中:
图 2.378
• 角系数的总和 - 由于离开表面的辐射是守恒的,因此给定表面

的所有角系数之和恒等于 1。对于
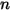
个表面构成的封闭系统,可以得到:
方程 2.305
• 自视表面 - 由于辐射沿直线传播,因此,凸表面中没有任何辐射光线可以在离开表面后再入射到同一表面。因此,无法自视凸表面:
方程 2.306
对于凹表面,表面上一个位置的出射光线之后可入射到同一表面的另一位置。因此,凹表面对其自身可见:
方程 2.307
• 叠加 - 对于由
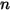
个表面构成的系统,如果给定表面

将能量辐射到
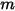
个表面 (
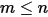
),则表面

和
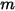
个表面之间的角系数等于表面

和
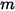
个表面中每个表面之间的角系数之和:
方程 2.308
如果未针对几何提供给定图表或图形,则叠加规则或求和规则将十分有用。通过叠加规则,可以使用已知的几何之和或之差来表示正在求解的几何。
• 互易性 -
方程 2.304 将角系数
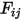
定义为离开表面

与到达表面
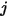
的辐射能占比。同样,角系数
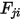
即指离开表面
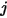
与到达表面

的能量占比,其表示如下:
方程 2.309
方程 2.310
方程 2.310 称为角系数的互易性。通过互易性定理,可以直接计算其中一对角系数。
聚类
当辐射表面的数量很多时,使用 S2S 辐射模型进行计算的成本会很高。要缩短计算时间和降低存储需求,可以通过对一定数量的相邻边界单元面进行分组来创建表面簇,以减少辐射表面的数量。然后,计算表面簇的辐射度 (
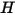
)。随后,再将这些值分配给每个簇内的边界单元面上来计算壁温。由于辐射源项是高度非线性的 (与温度的四次方成正比),因此,请确保计算表面簇的平均温度,并使通量和源项在形成簇的边界面上适当分布。
表面簇温度是通过计算边界面温度的面积平均值得到的,如下列方程所示:
方程 2.311
其中,
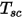
是表面簇的温度,
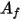
和
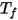
分别是 CFA 仿真中边界单元面的面积和温度。对表面簇内的所有面进行求和运算。
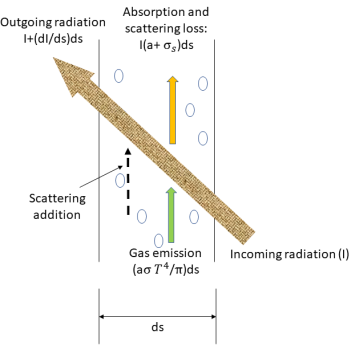

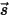 方向上的增量厚度为 ds,如图所示。穿过介质层后,位置
方向上的增量厚度为 ds,如图所示。穿过介质层后,位置 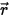 ⃗ 和方向
⃗ 和方向 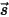 上的入射光线有四种变化方式,其作用在于增强 (能量获得 +) 或减弱 (能量损失 -) 辐射强度
上的入射光线有四种变化方式,其作用在于增强 (能量获得 +) 或减弱 (能量损失 -) 辐射强度 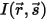 :
: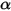 ,则通过吸收损失的辐射能量为:
,则通过吸收损失的辐射能量为: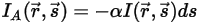
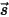 )。如果散射系数为
)。如果散射系数为 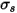 ,则通过散射损失的辐射能量为:
,则通过散射损失的辐射能量为: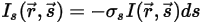
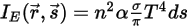
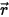 和
和 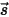 而定。引入
而定。引入 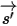
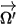 来表示辐射束的方向和立体角,以及引入
来表示辐射束的方向和立体角,以及引入 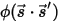 来表示相位函数之后,各个方向上传播的光线散射到
来表示相位函数之后,各个方向上传播的光线散射到 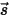 ⃗ 方向的强度分量如下:
⃗ 方向的强度分量如下: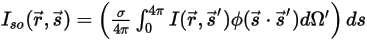
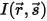 ,而出射辐射强度为
,而出射辐射强度为 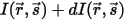 ,则
,则 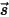 ⃗ 方向上的辐射能量平衡具有如下形式:
⃗ 方向上的辐射能量平衡具有如下形式: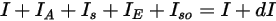
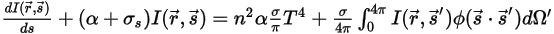
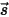 上辐射强度
上辐射强度 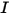 的一阶积分微分方程。要在域中求解此方程,需要给出域中的温度场,同时还需要给出内部和外部表面上
的一阶积分微分方程。要在域中求解此方程,需要给出域中的温度场,同时还需要给出内部和外部表面上 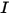 的边界条件,以及两种不同介质之间的界面。
的边界条件,以及两种不同介质之间的界面。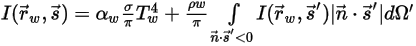
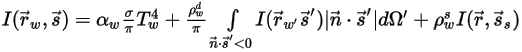
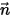 ⃗
⃗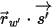 处表面的单位法向矢量
处表面的单位法向矢量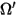
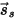
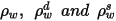
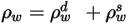
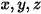 表示的辐射强度传输方程,并针对与矢量方向
表示的辐射强度传输方程,并针对与矢量方向 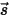 关联的有限个离散立体角进行求解。所选的立体角数量直接决定了精度和计算成本。DO 建模方法也与流体流和能量方程所使用的方法相同。目前,该模型是涵盖整个光学厚度范围的最为常见的一种辐射模型,适合解决从表面对表面辐射到介质参与辐射 (如燃烧系统) 等问题。但是,对于非灰辐射,DO 模型的计算成本很高。
关联的有限个离散立体角进行求解。所选的立体角数量直接决定了精度和计算成本。DO 建模方法也与流体流和能量方程所使用的方法相同。目前,该模型是涵盖整个光学厚度范围的最为常见的一种辐射模型,适合解决从表面对表面辐射到介质参与辐射 (如燃烧系统) 等问题。但是,对于非灰辐射,DO 模型的计算成本很高。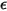 和吸收率
和吸收率 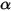 均与出射光线和入射光线的波长无关。根据基尔霍夫热辐射定律 (方程 2.274),发射率等于吸收率:
均与出射光线和入射光线的波长无关。根据基尔霍夫热辐射定律 (方程 2.274),发射率等于吸收率: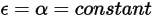
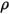 ) 相对于立体角各向同性。根据方程 2.290,表面反射率的计算方式如下:
) 相对于立体角各向同性。根据方程 2.290,表面反射率的计算方式如下: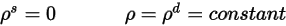
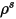
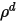
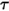 同样与波长无关:
同样与波长无关: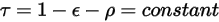
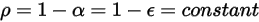
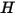 ,即每单位面积的发射功率 (发射率)
,即每单位面积的发射功率 (发射率) 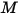 和表面每单位面积所接收的辐射功率的反射分量 (辐照度)
和表面每单位面积所接收的辐射功率的反射分量 (辐照度) 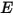 之和:
之和: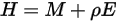
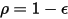 ),辐射度为:
),辐射度为: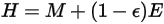
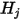 表示任意表面
表示任意表面 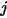 的辐射度,
的辐射度,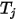 是表面温度,而
是表面温度,而 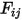 是表面
是表面 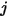 和
和  之间的角系数,则表面
之间的角系数,则表面  的辐射度为:
的辐射度为: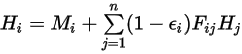
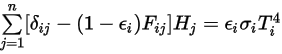
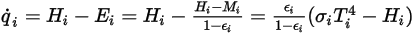
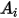 ,离开表面的净辐射热流
,离开表面的净辐射热流 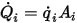 的计算公式为:
的计算公式为: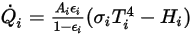
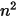 个角系数。此过程非常耗时,特别是表面数量越多,计算越耗时。
个角系数。此过程非常耗时,特别是表面数量越多,计算越耗时。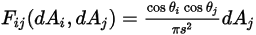
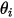 和
和 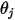 分别是两个微分面积上表面法向与光线之间的夹角。
分别是两个微分面积上表面法向与光线之间的夹角。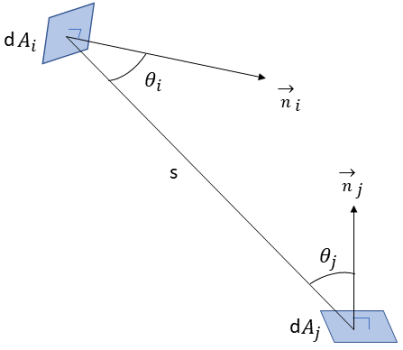
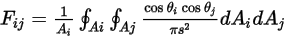
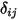 来表示
来表示 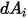 和
和 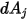 之间的可见性:
之间的可见性: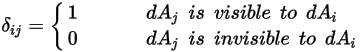
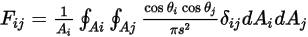
 的所有角系数之和恒等于 1。对于
的所有角系数之和恒等于 1。对于 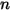 个表面构成的封闭系统,可以得到:
个表面构成的封闭系统,可以得到:
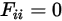
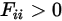
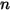 个表面构成的系统,如果给定表面
个表面构成的系统,如果给定表面  将能量辐射到
将能量辐射到 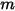 个表面 (
个表面 (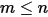 ),则表面
),则表面  和
和 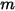 个表面之间的角系数等于表面
个表面之间的角系数等于表面  和
和 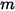 个表面中每个表面之间的角系数之和:
个表面中每个表面之间的角系数之和: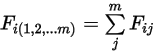
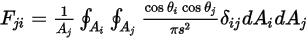
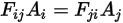
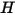 )。随后,再将这些值分配给每个簇内的边界单元面上来计算壁温。由于辐射源项是高度非线性的 (与温度的四次方成正比),因此,请确保计算表面簇的平均温度,并使通量和源项在形成簇的边界面上适当分布。
)。随后,再将这些值分配给每个簇内的边界单元面上来计算壁温。由于辐射源项是高度非线性的 (与温度的四次方成正比),因此,请确保计算表面簇的平均温度,并使通量和源项在形成簇的边界面上适当分布。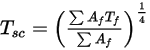
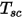 是表面簇的温度,
是表面簇的温度,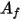 和
和 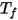 分别是 CFA 仿真中边界单元面的面积和温度。对表面簇内的所有面进行求和运算。
分别是 CFA 仿真中边界单元面的面积和温度。对表面簇内的所有面进行求和运算。