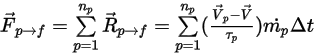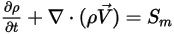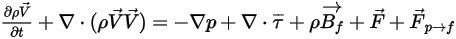离散粒子模型
在离散粒子模型中,借助跟踪穿过连续流体相的指定粒子数来建立离散相流动模型。在 Creo Flow Analysis 中,此模型有以下假设和限制:
• 一定数量的球形粒子穿过连续流体流相。这些粒子被定义为“有质量”(Has Mass) 或“无质量”(Massless)。
• 释放位置和时间下的指定半径确定了粒子的大小,该大小保持不变。粒子间相互作用可忽略不计。
• 粒子与流体流和壁边界相互作用。粒子体积不会置换任何流体 (粒相的低体积分数) 或干涉几何 (超大粒子穿过较小的间隙)。
• 连续流体相和粒子之间不会发生热质传递。假定粒子温度与流体流的局部温度相同。
在这些假设下,将使用 Lagrangian 方法跟踪每个单独粒子的运动。针对每个粒子形成一组有关时间的常微分方程 (包含位置和速度方程),以此来执行跟踪。然后,对这些方程进行积分来计算粒子遍历流域时的反应。Creo Flow Analysis 中粒子建模方法的特点如下:
• 离散粒子模型遵照欧拉-拉格朗日方法。通过求解连续性和纳维-斯托克斯方程,可将流体相视为一个连续体。通过使用拉格朗日力学方法跟踪每个单独粒子的运动,可求解离散相。粒子占用的体积分数并不纳入连续相计算中。
• 对于设置为“无质量”(Massless) 的粒子,它们会随着流体流移动,或沿流场的流线移动。粒子的大小或半径并不会影响流体或粒子,而是仅供显示之用。
• 对于设置为“有质量”(Has Mass) 的粒子,其质量取决于为指定的粒子半径或直径指定的值以及粒子密度。作用在粒子上的力 (可确定粒子的运动) 包括粒子与流体间的阻力 (惯性力) 和重力。不考虑作用在粒子上的湍流分散力。粒子的大小会影响粒子与流体间的阻力和后处理过程。
• 流体相与离散粒相之间的动量交换将通过以下方式建模:
◦ 单向耦合 - 只有流体相会影响粒子的运动。
◦ 双向耦合 - 粒子也会通过粒子与流体间的阻力影响流体流。
• 使用粒子壁模型 (例如,粘附反弹、理想反弹和部分反弹) 对壁与粒子间的相互作用进行建模。
• 虽然流体相可以是稳态,也可以是非稳态,但粒子跟踪是一个瞬态过程,在此过程中会涉及通过离散化域对粒子路径进行积分。在此方法中,将在不同时间从指定位置释放或喷射单个粒子。将从每个粒子的释放位置开始一直跟踪到其目标位置,此目标位置为粒子逸出域外或满足特定积分限制的位置。最后,将求得所有粒子轨迹的平均值,并将粒子与流体间的相互作用作为流体相动量方程的源项进行计算。
• 使用“粒子”(Particle) 模块中的相关脉线跟踪方法,显示粒子的行进路径。
粒子运动理论
在 Lagrange 方法中,粒子运动由粒子上的力平衡和粒子的释放条件 (初始条件) 来确定。要对离散粒相进行建模,首先需要根据力平衡构建粒子运动方程。然后,指定粒子的边界和初始条件。最后,对粒子运动方程进行积分运算,以便实现粒子跟踪。
粒子运动方程
• 粒子力平衡
对于在连续流体介质中移动的离散粒子,粒子的运动由作用在其上的净力决定。根据牛顿第二定律,可以采用以下拉格朗日形式表示粒子上的力平衡:
方程 2.366
其中,
| 粒子质量 (kg) |
| 粒子速度 (m/s) |
| 作用在粒子上的净力 (N),这会影响粒子加速度 |
在笛卡尔坐标系中,如果
点 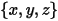 | 粒子的位置 |
| 粒子速度分量 |
使用 Lagrangian 方法时,粒子速度
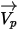
的定义如下:
方程 2.367
对于以密度
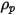
和直径
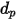
(
Creo Flow Analysis 接受半径作为输入) 占用体积
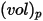
的球形粒子,按以下方式计算粒子质量
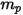
:
方程 2.368
对于净力
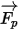
,影响因素如流体对粒子的阻力、重力作用以及由于域旋转而产生的力 (离心力和科氏力)。附加影响因素即由于粒子与流体之间的速度差以及由于流体受到粒子作用而发生位移时所产生的其他力。在
Creo Flow Analysis 中,
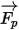
可表示为如下形式:
方程 2.369
其中,
| 阻力 (N) |
| 重力 (N) |
| 其他力,例如用户指定的虚拟质量力、压力梯度力、升力 (n) 等 |
默认情况下,仅考虑作用于粒子的阻力。
方程 2.370
要使
方程 2.370 封闭,需要计算每个单独力产生的作用。下面将介绍
Creo Flow Analysis 中采用的子模型或公式:
◦ 施加于粒子的阻力
作用在粒子上的气动阻力与相滑移速度 (流体与粒子速度之间的差值) 成正比。假定粒子在给定时间内与流体处在同一空间内,流体的流动速度等于
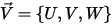
,则阻力可表示为如下形式:
方程 2.371
其中,
对于直径为
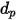
的球形粒子,
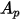
是最大的横截面面积:
方程 2.372
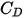
是阻力系数,取决于相对雷诺数
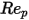
:
方程 2.373
其中,
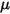
是流体动力黏度 (Pa-s)。
引入阻力系数
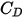
,可解释有关实心球体粘性阻力的实验结果。运用各种模型或经验关联式,可确定阻力函数
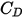
(
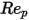
),进而可估算流体与粒子间的交换量。对于光滑球形粒子,在许多模型中,最完整的

函数是由 Morsi 和 Alexander 修正得到,
参考资料:S. A. Morsi and A. J. Alexander, "An Investigation of Particle Trajectories in Two-Phase Flow Systems", J. Fluid Mech., 55(2) 193–208, September 26 1972.
其一般表达式如下:
方程 2.374
其中,
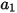
、
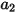
和

为模型常数,它们的值取决于相对雷诺数,如下表所示:
| | | |
0 < 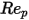 <=0.1 | 0 | 24 | 0 |
0.1 < 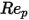 <=1 | 3.690 | 22.73 | 0.0903 |
1< 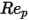 <=10 | 1.222 | 29.1667 | -3.8889 |
10 < 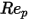 <=100 | 0.6167 | 46.50 | -116.67 |
100 < 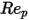 <=1000 | 0.3644 | 98.33 | -2778 |
1000 < 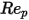 <=5000 | 0.357 | 148.62 | -47500 |
5000 < 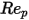 <=10000 | 0.46 | -490.546 | 578700 |
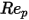 >10000 | 0.5191 | -1662.5 | 5416700 |
该表显示,在极低粒子雷诺数 (粘性流态) (即
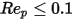
) 下,流经球形粒子的流动阻力系数仍符合斯托克斯定律:
方程 2.375
相反,如果
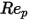
足够大,使惯性效应在粘性效应中占主导,则流体与粒子间的流动处于惯性流态或牛顿流态。在该表中,可以观察到阻力系数与相对雷诺数的相关性变小。此外,通常会使用
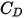
的常数值,而不是完整的 Morsi 和 Alexander 模型:
方程 2.376
在粘性流态与惯性流态之间的过渡区域 (
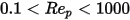
) 中,粘性效应和惯性效应两者对于球形粒子而言都很重要。因此,阻力系数是关于相对雷诺数的复杂函数,可通过 Morsi 和 Alexander 模型或其他关联式估算得到。例如,根据 Schiller 和 Naumann 模型:
参考资料:L. Schiller and Z. Naumann, "Z. Ver. Deutsch. Ing. 77. 318. 1935.
方程 2.377
方程 2.378
方程 2.379
因此,默认的 (仅考虑阻力) 粒子力平衡方程可表示如下:
方程 2.380
• 包含重力项
默认情况下,粒子力平衡方程中不含重力项。可以在
Creo Flow Analysis 中激活重力项。对于浸没在流体流中的粒子,重力效应会产生浮力,该浮力等于由粒子置换的流体重量。假定
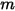
是由粒子置换的流体质量,而
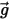
是重力矢量,则由此产生的力如下:
方程 2.381
或将每单位粒子质量的力指定为:
方程 2.382
力平衡方程的形式如下:
方程 2.383
• 施加于粒子的旋转力
对于旋转参考系中的流体流动模型,旋转引起的附加力项
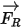
是粒子加速度固有的一部分。它由科氏力和向心力效应构成:
方程 2.384
或将每单位粒子质量的旋转力指定为:
方程 2.385
其中,
添加此力项后,粒子平衡方程变为:
方程 2.386
当在旋转参考系中求解流动时,
方程 2.386 用于控制粒子在 Lagrange 系统中的运动。
粒子的边界和初始条件
在 Lagrange 方法中,粒子跟踪是一个瞬态过程。因此,需要使用边界和初始条件才能计算粒子的轨迹。边界条件用于定义计算域边界处的粒子反应,尤其是粒子与壁之间的相互作用。初始条件可确定粒子在边界处的释放情况,其中包括释放位置、频率、速度、粒子类型和大小 (半径) 以及粒子数。
边界条件
Creo Flow Analysis 提供离散相边界条件,用以确定粒子在边界处的反应。当粒子到达流域边界 (包括物理边界和固体-流体界面),例如壁或入口边界时,将会出现下列情况之一:
• 粒子通过弹性或非弹性碰撞发生反射。
• 粒子通过边界逸出,因此不纳入边界撞击点的计算中。
• 粒子被壁面俘获,因此不纳入边界撞击点的计算中。
• 粒子穿过内部边界区域,如风扇或多孔介质阶跃面。
• 粒子与边界之间的相互作用由用户定义的方法来确定,以对粒子撞击边界时的粒子反应进行建模。
根据边界处的粒子反应,将流动边界条件和界面重新分组为三类离散粒子边界条件:开放、对称和壁。
• 开放离散粒子边界
粒子或流线可流出计算域。开放边界是欧拉系统中流体流相的入口或出口边界。它也可应用于流动边界,例如,壁和对称。在开放粒子边界处,粒子会根据粒子速度方向流出或进入域。
设
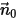
为开放边界的单位法矢量,该矢量指向计算域之外,且粒子边界速度为
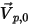
。如果
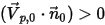
,则速度矢量
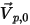
指向计算域之外。这表示粒子穿过边界逸出,因此不纳入边界撞击点的计算中。
• 对称粒子边界
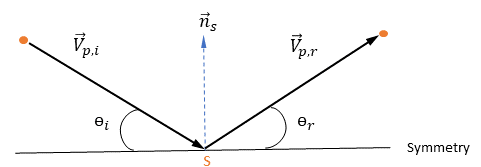
当计算域中的粒子或脉线撞击离散对称边界时,边界条件会将其反射回域中。对于离散粒相,对称粒子边界通常与欧拉系统中的流动对称相对应。它也可以是粒子的释放位置。
设
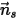
为对称在点
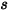
处的法向-对称单位矢量,且其方向背离对称,指向计算域之外。引入
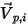
和
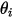
,用以表示粒子对称边界处的粒子撞击速度角,如下图所示。当粒子发生对称反射时,其总动能守恒:切向速度保持不变,而法向速度分量仅更改符号。粒子对称边界条件可表示如下:
方程 2.387
其中,
| 点 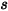 处的角度:对称 (度) |
| 粒子入射速度的大小 (m/s) |
| 粒子反射速度的大小 (m/s) |
• 壁粒子边界
对于液滴,液滴与壁之间的相互作用取决于壁温、壁材料和粗糙度、撞击角度和撞击速度、是否存在壁膜以及各种其他参数。因此,将使用一系列子模型来重现壁与粒子间相互作用的不同流态,并解释流动参数和壁边界条件的影响。
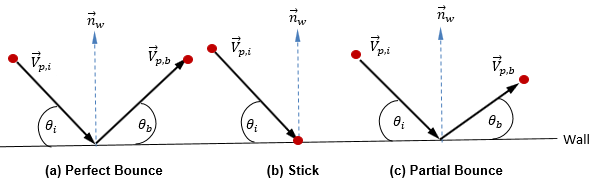
在当前离散粒子模型中,假设粒子的形状、大小和质量保持不变。此外,还应考虑流体和粒子处于热平衡。因此,使用一种简单方法来描述 (有质量) 粒子与壁的碰撞过程:在碰撞过程中,粒子仅与壁交换动量,而粒子与壁之间有三种作用方式。这三种方式即理想反弹、粘附反弹和部分反弹。
◦ 理想反弹 - 粒子或脉线在撞击到壁时发生反射。粒子的动量和动能完全守恒。入射角等于反射角,而壁法向速度分量会更改符号:
方程 2.388
其中,
| 壁法向单位矢量 |
| 壁边界处的角度 (度) |
| 粒子入射速度的大小 (m/s) |
| 粒子反弹速度的大小 (m/s) |
◦ 粘附 - 粒子碰撞壁,失去其所有动量和能量,进而粘附在壁上:
如果不考虑粒子沿壁面的积聚,则粒子将完全不纳入边界撞击点的计算中。
◦ 部分反弹 - 介于理想反弹与粘附反弹之间的壁粒子条件。粒子或脉线虽然在壁处发生反弹,但还是会在法向和/或切向方向上损失一部分能量。粒子的动量和动能不守恒,且入射角通常大于反射角:
通过粒子与壁之间的相互作用产生的能量损失由用户输入来指定:
▪ 法向能量损失 - 指定粒子在壁上损失的动能法向分量。
▪ 切向能量损失 - 指定粒子在壁上损失的动能切向分量。
在
Creo Flow Analysis 中,是粒子反弹还是粘附需由指定的最大和最小法向速度值来确定。假定
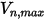
是指定的粒子最大法向速度,而
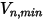
是指定的粒子最小法向速度,且条件如下:
▪ 如果
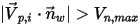
或
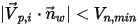
,则粒子会在壁处反弹。
▪ 如果
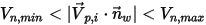
,则粒子会粘附在壁上。
粒子与壁之间相互作用模型仅适用于设为 Has mass 的粒子。无质量的粒子会沿壁随着流线移动。
请注意,粒子壁边界可以是外壁和流-固界面。与开放和对称粒子边界一样,粒子可以从壁边界释放。
初始条件 (释放粒子)
初始条件为所有离散相因变量提供起始值,这些因变量用于描述单个粒子的瞬时条件。对于 Lagrange 系统粒子跟踪,确定初始条件的过程包括从边界 (开放、对称、壁和界面) 释放粒子 (频率和分布),以及为每个粒子分配属性。
激活“释放粒子”(Release Particle) 时,下列参数或变量是粒子运动的初始条件:
粒子运动方程的积分
要跟踪粒子运动,可在 Lagrange 系统中对每个粒子的轨迹方程进行解析求解或数值求解 (积分)。根据
方程 2.367 和
方程 2.386,运动方程改写如下:
方程 2.391
方程 2.392
其中,
| 粒子的位置矢量 |
| 包括加速度,由除了阻力之外的其他所有力 (如重力、旋转效应等) 引起的 |
方程 2.391 和
方程 2.392 是一组耦合的常微分方程。根据给定的初始条件和边界条件,对时间步长
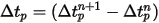
内的粒子速度进行正向欧拉积分,由此计算粒子位移 (
方程 2.391):
方程 2.393
其中,
在首个时间步长处,
其中,
方程 2.394
在此正向积分方法中,假定在时间步长开始时计算的粒子速度在整个步长内最大。在时间步长结束时,将通过求解粒子动量 (
方程 2.392) 来计算新的粒子速度。假定
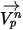
、
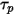
和
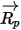
在时间段
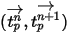
内为常数,且流体属性取自时间步长开始时间
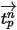
,则
方程 2.392 的解析解为:
方程 2.395
要计算
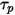
和
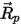
,需要用到粒子所在位置处的密度、黏度和速度等流体变量。它们被视为粒子当前所在的流体流相的单元值。此解析方案虽然高效,但对于较大时间步长以及粒子与连续流体流不处于流体动力平衡的情况,该方法可能会变得不太准确。在这种情况下,将使用数值方案对
方程 2.392 进行积分。
粒子-流体耦合
在欧拉-拉格朗日方法中,假定连续流体流通过力、热和质量传递影响粒子反应。例如,粒子力平衡
方程 2.370 中的力项
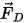
会考虑流体对粒子的气动阻力。虽然将粒相视为离散相且不会以体积形式置换流体,但粒子可以通过动量交换也有可能是质量和热量交换对流体流产生反作用。粒子对流体的影响称为粒子-流体耦合。这种耦合分为两类:
• 单向耦合
单向耦合允许流体影响粒子的轨迹,但粒子不会对流体产生任何影响。对于无质量的粒子,粒子与流体间的相互作用为单向耦合:粒子会随着流体流移动。对于有质量的粒子,单向耦合可以是具有低离散相负载的流中可接受的近似结果,其中粒子对流体流的影响可忽略不计。
对于连续流体相,流场将作为单相流体流进行计算,其中不存在离散粒相。然后,根据计算出的流场和初始条件来跟踪粒子运动。对于稳态流,会通过求解连续性和纳维-斯托克斯方程获得连续相流的收敛解之后进行粒子跟踪。对于瞬态流仿真,系统会在流仿真的每个时间步长结束时跟踪粒子运动。
• 双向耦合
对于有质量的粒子,双向耦合允许流体影响粒子的轨迹。它还会考虑粒子对连续流体相的影响。如果不考虑热质传递,则流体与粒子之间的双向相互作用将仅与动量交换有关。对于从连续相传递到离散相的动量,可通过跟踪每个单独粒子穿过控制体积块时获得或损失的动量来计算。在双向耦合中,需要将粒子与流体间的动量交换纳入流体的动量方程中,才能解释离散相轨迹对连续体的影响。在
方程 2.386 中,仅阻力可以解释粒子与流体间的动量交换,因此将其纳入动量方程中。请注意,对于无质量的粒子,不会计算流体流与其之间的任何交换项,因此,离散相轨迹不会对连续体产生影响。
要将粒子与流体间的阻力效应纳入连续相动量方程中,则需将通过流体的每个移动粒子的阻力施加于此时间步长内粒子所在的控制体积块中。对于粒子
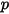
,根据以下微分方程计算其由阻力
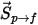
引起的动量源:
方程 2.396
连续相的粒子源是与该粒子的数值流率 (质量流率除以粒子质量) 相乘的源项
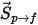
:
方程 2.397
其中,
假定
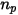
是在时间步长
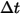
处穿过控制体积块的粒子数,则粒子与流体间的总源项为:
方程 2.398
纳入流体与粒子间的阻力之后,针对连续相求解的控制方程现表示如下:
方程 2.399
方程 2.400
对于单向耦合,
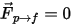
连续流体相受精确的单相连续性和动量方程控制。对于双向耦合,其中包含附加的粒子与流体间阻力源项。
方程 2.399 和
方程 2.400 的求解方法与单相流相同。
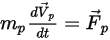
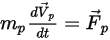
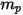
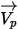
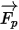
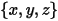
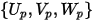
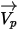 的定义如下:
的定义如下: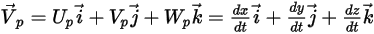
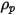 和直径
和直径 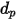 (Creo Flow Analysis 接受半径作为输入) 占用体积
(Creo Flow Analysis 接受半径作为输入) 占用体积 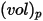 的球形粒子,按以下方式计算粒子质量
的球形粒子,按以下方式计算粒子质量 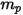 :
: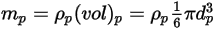
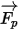 ,影响因素如流体对粒子的阻力、重力作用以及由于域旋转而产生的力 (离心力和科氏力)。附加影响因素即由于粒子与流体之间的速度差以及由于流体受到粒子作用而发生位移时所产生的其他力。在 Creo Flow Analysis 中,
,影响因素如流体对粒子的阻力、重力作用以及由于域旋转而产生的力 (离心力和科氏力)。附加影响因素即由于粒子与流体之间的速度差以及由于流体受到粒子作用而发生位移时所产生的其他力。在 Creo Flow Analysis 中,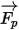 可表示为如下形式:
可表示为如下形式: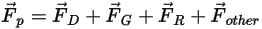
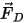
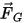
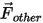
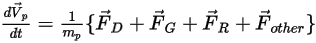
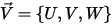 ,则阻力可表示为如下形式:
,则阻力可表示为如下形式: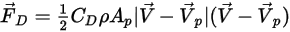
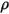
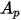
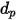 的球形粒子,
的球形粒子,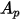 是最大的横截面面积:
是最大的横截面面积: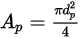
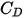 是阻力系数,取决于相对雷诺数
是阻力系数,取决于相对雷诺数 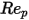 :
: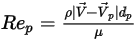
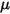 是流体动力黏度 (Pa-s)。
是流体动力黏度 (Pa-s)。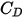 ,可解释有关实心球体粘性阻力的实验结果。运用各种模型或经验关联式,可确定阻力函数
,可解释有关实心球体粘性阻力的实验结果。运用各种模型或经验关联式,可确定阻力函数 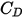 (
(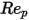 ),进而可估算流体与粒子间的交换量。对于光滑球形粒子,在许多模型中,最完整的
),进而可估算流体与粒子间的交换量。对于光滑球形粒子,在许多模型中,最完整的  函数是由 Morsi 和 Alexander 修正得到,
函数是由 Morsi 和 Alexander 修正得到,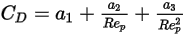
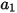 、
、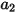 和
和  为模型常数,它们的值取决于相对雷诺数,如下表所示:
为模型常数,它们的值取决于相对雷诺数,如下表所示: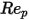
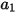
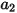
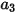
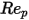 <=0.1
<=0.1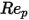 <=1
<=1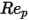 <=10
<=10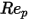 <=100
<=100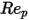 <=1000
<=1000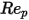 <=5000
<=5000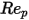 <=10000
<=10000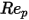 >10000
>10000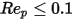 ) 下,流经球形粒子的流动阻力系数仍符合斯托克斯定律:
) 下,流经球形粒子的流动阻力系数仍符合斯托克斯定律:
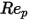 足够大,使惯性效应在粘性效应中占主导,则流体与粒子间的流动处于惯性流态或牛顿流态。在该表中,可以观察到阻力系数与相对雷诺数的相关性变小。此外,通常会使用
足够大,使惯性效应在粘性效应中占主导,则流体与粒子间的流动处于惯性流态或牛顿流态。在该表中,可以观察到阻力系数与相对雷诺数的相关性变小。此外,通常会使用 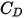 的常数值,而不是完整的 Morsi 和 Alexander 模型:
的常数值,而不是完整的 Morsi 和 Alexander 模型: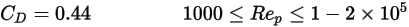
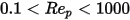 ) 中,粘性效应和惯性效应两者对于球形粒子而言都很重要。因此,阻力系数是关于相对雷诺数的复杂函数,可通过 Morsi 和 Alexander 模型或其他关联式估算得到。例如,根据 Schiller 和 Naumann 模型:
) 中,粘性效应和惯性效应两者对于球形粒子而言都很重要。因此,阻力系数是关于相对雷诺数的复杂函数,可通过 Morsi 和 Alexander 模型或其他关联式估算得到。例如,根据 Schiller 和 Naumann 模型: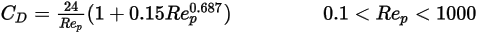
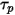 :
: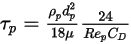
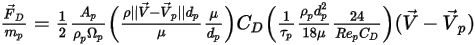
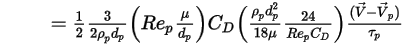
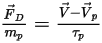
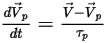
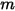 是由粒子置换的流体质量,而
是由粒子置换的流体质量,而 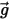 是重力矢量,则由此产生的力如下:
是重力矢量,则由此产生的力如下: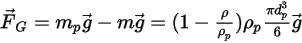
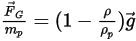
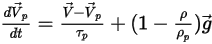
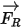 是粒子加速度固有的一部分。它由科氏力和向心力效应构成:
是粒子加速度固有的一部分。它由科氏力和向心力效应构成: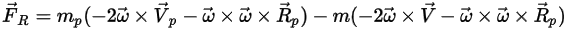
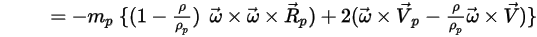
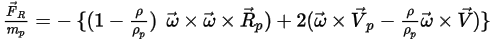
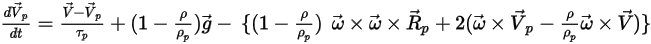
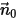 为开放边界的单位法矢量,该矢量指向计算域之外,且粒子边界速度为
为开放边界的单位法矢量,该矢量指向计算域之外,且粒子边界速度为 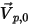 。如果
。如果 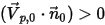 ,则速度矢量
,则速度矢量 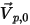 指向计算域之外。这表示粒子穿过边界逸出,因此不纳入边界撞击点的计算中。
指向计算域之外。这表示粒子穿过边界逸出,因此不纳入边界撞击点的计算中。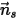 为对称在点
为对称在点 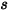 处的法向-对称单位矢量,且其方向背离对称,指向计算域之外。引入
处的法向-对称单位矢量,且其方向背离对称,指向计算域之外。引入 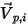 和
和 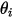 ,用以表示粒子对称边界处的粒子撞击速度角,如下图所示。当粒子发生对称反射时,其总动能守恒:切向速度保持不变,而法向速度分量仅更改符号。粒子对称边界条件可表示如下:
,用以表示粒子对称边界处的粒子撞击速度角,如下图所示。当粒子发生对称反射时,其总动能守恒:切向速度保持不变,而法向速度分量仅更改符号。粒子对称边界条件可表示如下: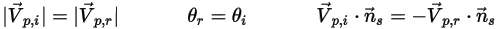
 处的角度:对称 (度)
处的角度:对称 (度)
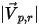
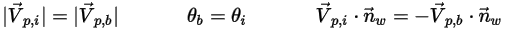
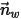
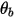
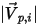
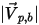
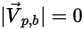
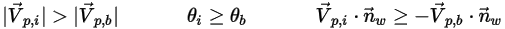
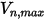 是指定的粒子最大法向速度,而
是指定的粒子最大法向速度,而 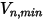 是指定的粒子最小法向速度,且条件如下:
是指定的粒子最小法向速度,且条件如下: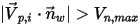 或
或 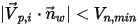 ,则粒子会在壁处反弹。
,则粒子会在壁处反弹。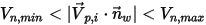 ,则粒子会粘附在壁上。
,则粒子会粘附在壁上。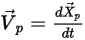
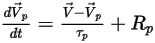
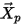
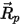
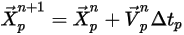
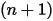
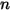
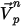
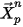
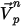

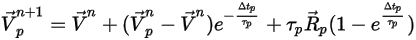
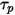 和
和 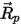 ,需要用到粒子所在位置处的密度、黏度和速度等流体变量。它们被视为粒子当前所在的流体流相的单元值。此解析方案虽然高效,但对于较大时间步长以及粒子与连续流体流不处于流体动力平衡的情况,该方法可能会变得不太准确。在这种情况下,将使用数值方案对方程 2.392 进行积分。
,需要用到粒子所在位置处的密度、黏度和速度等流体变量。它们被视为粒子当前所在的流体流相的单元值。此解析方案虽然高效,但对于较大时间步长以及粒子与连续流体流不处于流体动力平衡的情况,该方法可能会变得不太准确。在这种情况下,将使用数值方案对方程 2.392 进行积分。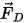 会考虑流体对粒子的气动阻力。虽然将粒相视为离散相且不会以体积形式置换流体,但粒子可以通过动量交换也有可能是质量和热量交换对流体流产生反作用。粒子对流体的影响称为粒子-流体耦合。这种耦合分为两类:
会考虑流体对粒子的气动阻力。虽然将粒相视为离散相且不会以体积形式置换流体,但粒子可以通过动量交换也有可能是质量和热量交换对流体流产生反作用。粒子对流体的影响称为粒子-流体耦合。这种耦合分为两类: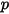 ,根据以下微分方程计算其由阻力
,根据以下微分方程计算其由阻力 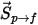 引起的动量源:
引起的动量源: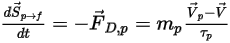
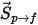 :
: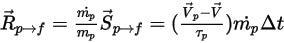
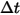
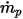
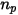 是在时间步长
是在时间步长 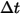 处穿过控制体积块的粒子数,则粒子与流体间的总源项为:
处穿过控制体积块的粒子数,则粒子与流体间的总源项为: