Flussmodelle
Das Modul Flow löst die Erhaltung von Masse und Impuls unter Verwendung der transienten Navier-Stokes-Gleichungen H.Ding, F.C. Visser, Y.Jiang und M. Furmanczyk, "Demonstration and Validation of a 3-D CFD Simulation Tool Predicting Pump Performance and Cavitation for Industrial Applications", FEDSM2009-78256, 2009..
Die integrale Form (konservativ) der Reynolds-gemittelte Navier-Stokes-Gleichungen (Reynold’s Averaged Navier-Stokes Equations, RANS) lautet wie folgt:
• Stetigkeit
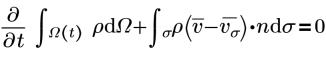
• Impuls
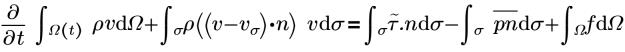
• Spannungstensor
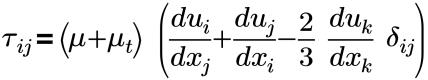
Dabei gilt:
τij | Effektive Scherspannung (molekular + turbulent) |
f | Volumenkraft |
n | Flächennormale |
ρ | statischer Druck (Pa) |
t | Zeit |
v | Flüssigkeitsgeschwindigkeit |
vσ | Netzgeschwindigkeit |
Ω(t) | Steuervolumen als Funktion der Zeit |
r | Durchschnittliche lokale Flüssigkeitsdichte (kg/m3) |
σ | Fläche des Steuervolumens |
µ | Dynamische Viskosität (Poise oder PA-s) |
µt | Turbulente dynamische Viskosität |
δij | Kronecker-Delta (=1 für i=j, =0 für i≠j) |
Viskositätsmodelle
• Konstante dynamische Viskosität (Constant Dynamic Viscosity) – Gibt die Viskosität (Viscosity) der Flüssigkeit in einem ausgewählten Volumen an. Die Einheit der dynamischen Viskosität ist Pa-s oder N-s/m2.
Der Wert der dynamischen Viskosität wird im Feld unter der Auswahl Konstante dynamische Viskosität (Constant Dynamic Viscosity) angegeben.
• Konstante kinematische Viskosität (Constant Kinematic Viscosity) – Gibt die Viskosität (Viscosity) der Flüssigkeit in einem ausgewählten Volumen an. Die Einheit der kinematischen Viskosität ist m2/s. Der Wert der kinematischen Viskosität wird im Feld unter der Auswahl Constant Kinematic Viscosity angegeben.
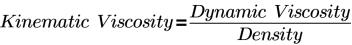
• Sutherland Law – Gibt die Viskosität der Flüssigkeit in einem ausgewählten Volumen durch dynamische Viskosität (Pa-s) an. Die Gleichung und die Eingaben sind wie folgt:
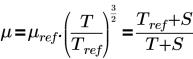
Dabei gilt:
T | Temperatur (K) |
µref | Viskosität bei Referenztemperatur (Pa-s) |
S | Sutherland-Temperatur (K) |
T ist die die Temperatur der Flüssigkeit (K), die als Eingabe benötigt wird, wenn das Energiemodul nicht aktiviert ist. |
Das Sutherland-Gesetz wird verwendet, um die Viskosität eines idealen Gases als Funktion der Temperatur zu berechnen. Sutherland, W. (1893), "The viscosity of gases and molecular force", Philosophical Magazine, S. 5, 36, pp. 507-531 (1893). Die folgende Tabelle zeigt die Sutherland-Konstanten- und Referenztemperatur für ausgewählte Gase. Ref: https://de.wikipedia.org/wiki/Viskosität.
Gas | S (K) | Tref (K) | mref (PA-s) |
|---|---|---|---|
Luft | 120 | 291.15 | 18.27 e-6 |
Stickstoff | 111 | 300.55 | 17.81 e-6 |
Sauerstoff | 127 | 292.25 | 20.81 e-6 |
Kohlendioxyd | 240 | 293.15 | 14.8 e-6 |
Kohlenmonoxid | 118 | 288.15 | 17.2 e-6 |
Wasserstoff | 72 | 293.85 | 8.76 e-6 |
Ammoniak | 370 | 293.15 | 9.82 e-6 |
Schwefeldioxid | 416 | 293.65 | 12.54 e-6 |
Helium | 79.4 | 273 | 19 e-6 |
Nicht newtonsche Viskositätsmodelle
Die nicht newtonschen Viskositätsmodelle sind:
• Herschel-Bulkley-Modell
• Bingham-Modelle
Diese Modelle stellen die entsprechende Viskosität für verschiedene Typen von Flüssigkeiten bereit, die nicht newtonsche Flusseigenschaften aufweisen. Das Herschel-Bulkley-Modell und die Bingham-Modelle verknüpfen die Scherspannung mit der Scherrate wie folgt:
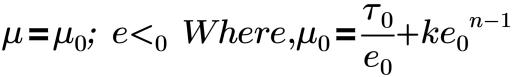
Dabei gilt:
e0 | Kritische Scherrate |
k | Konsistenzindex |
τ0 | Streckgrenze der Flüssigkeit |
n | Potenzgesetzindex. Für Bingham-Modell, n=1 |
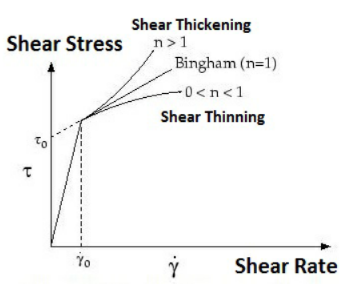
Die Scherrate von 0 entspricht dem Gamma-Punkt im Plot oben. |
Resistance Model
Widerstandsmodell (Resistance Model) ist eine Option des Moduls Fluss (Flow), die Sie zum Festlegen eines Widerstands in einem ausgewählten Volumen verwenden können. Das Widerstandsmodell (Resistance Model) enthält die folgenden beiden Modelle:
• Druckverlust (Pressure Loss): basierend auf der folgenden Gleichung:
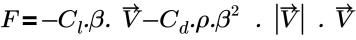
Dabei gilt:
Cl | Linearer Zugkoeffizient (Pa-s/m2) |
Cd | Quadratischer Zugkoeffizient (1/m) |
β | Porosität |
ρ | Dichte |
• Darcy-Gesetz (Darcy's Law): Modell basierend auf der folgenden Gleichung:
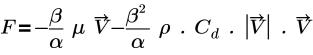
Dabei gilt:
β | Porosität |
α | Durchlässigkeit |
µ | Dynamische Viskosität |
V | Geschwindigkeit |
Cd | Quadratischer Zugkoeffizient (1/m) |
Die Geschwindigkeit, die in der Widerstandsgleichung verwendet wird, ist die lokale Geschwindigkeit. F in der Gleichung wird in der Einheit N/m3 gemessen, wie Kraft/Volumen oder Druckgradient (Dp/Dx) oder rg. Der Druckabfall für die Schnittstelle wird berechnet, indem F mit endlicher Dicke multipliziert wird. Die Porosität wird im Modul Allgemein (Common) festgelegt.