Discrete Particle Model
In the discrete particle model, flow of the dispersed phase is modeled by tracking a specified number of particles through the continuous fluid phase. In Creo Flow Analysis, the model has the following assumptions and restrictions:
• Definite number of spherical particles through the continuous fluid flow phase. The particles are defined as Has Mass or Massless.
• A specified radius at the release position and time determines the size of the particle, which remains unchanged. The particle-particle interaction is negligible.
• Particles interact with the fluid flow and wall boundaries. The volume of a particle does not displace any fluid (low volume fractions in the particle phase) or interfere with the geometry (an oversize particle fits through a smaller gap).
• No heat and mass transfer occurs between the continuous fluid phase and the particles. Particle temperature is assumed to be the same as the local temperature of the fluid flow.
Under these assumptions, the motion of each individual particle is tracked using the Lagrangian approach. Tracking is performed by forming a set of ordinary differential equations in time for each particle, consisting of equations for position and velocity. These equations are then integrated to calculate the reaction of the particles as they traverse the flow domain. The characteristics of the particle modeling approach in Creo Flow Analysis follow:
• The discrete particle model follows the Euler-Lagrange approach. The fluid phase is treated as a continuum by solving the continuity and Navier-Stokes equations. The dispersed phase is solved by tracking the motion of each individual particle using a Lagrangian approach. The fraction of volume taken by the particles is not included in the continuous phase calculation.
• Particles set to Massless move with the fluid flow, or follow the streamlines of the flow field. Particle size or radius does not impact the flow or particles and is for display only.
• For particles set to Has Mass, the mass is determined by values you specify for specified particle radius or diameter, and particle density. The forces that act on a particle, which determine the motion of particles, include particle-fluid drag (inertial force) and gravity. The turbulence dispersion forces on particles are not considered. The size of the particles influences the particle-fluid drag forces and postprocessing.
• Momentum exchange between the fluid phase and the discrete particle phases is modeled by the following:
◦ One-way coupling—Only the fluid phase affects the motions of particles.
◦ Two-way coupling—Particles also affect the fluid flow through particle-fluid drag forces.
• Wall-particle interactions are modeled using particle wall models such as stick, perfect bounce, and partial bounce.
• While the fluid phase can be steady and unsteady, particle tracking is a transient process that involves the integration of particle paths through the discretized domain. In this approach, individual particles are released or injected from specified locations at different times. Each particle is tracked from its release position to destination, where it escapes the domain or meets certain integration limits. Finally, an average of all particle tracks is obtained, and the particle-fluid interactions are calculated as source terms to the fluid phase momentum equations.
• Path traveled by particles appears using the related streakline tracking method in the Particle module.
Particle Motion Theory
In the Lagrange approach, particle motion is determined by the force balance on the particle and the conditions under which the particle is released (initial conditions). To model the discrete particle phase, the equations of motion for particles are first formed based on force balance. Then you specify the boundary and initial conditions for particles. Finally, the integration of particle equation of motion is carried out for particle tracking.
Equations of Motion for Particles
• Particle Force Balance
For a discrete particle traveling in a continuous fluid medium, the motion of the particle is determined by the net force acting on it. According to Newton’s second law, you can express the force balance on the particle in the following Lagrange form:
Equation 2.366
where,
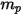 | particle mass kg |
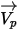 | particle velocity m/s |
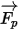 | net force exerted on the particle (N), which affects the particle acceleration |
In a Cartesian coordinate system, if
point 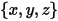 | location of the particle |
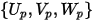 | particle velocity components |
With the Lagrangian approach, the particle velocity 
is defined as:
is defined as:
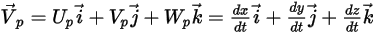
Equation 2.367
For a spherical particle that occupies a volume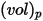 
with density 
and diameter 
(Creo Flow Analysis accepts radius as input), the particle mass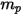 
is computed as:
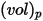with density and diameter (Creo Flow Analysis accepts radius as input), the particle mass 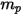is computed as: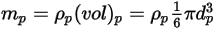
Equation 2.368
As for the net force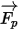 
, contributing factors such as the fluid-to-particle drag force, the gravity effect, and the forces due to domain rotation (centripetal and Coriolis forces). Additional contributing factors are other forces due to the difference in velocity between the particle and fluid, and to the displacement of the fluid by the particle. In Creo Flow Analysis 
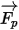can be expressed as follows:
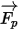, contributing factors such as the fluid-to-particle drag force, the gravity effect, and the forces due to domain rotation (centripetal and Coriolis forces). Additional contributing factors are other forces due to the difference in velocity between the particle and fluid, and to the displacement of the fluid by the particle. In Creo Flow Analysis 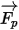can be expressed as follows: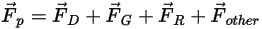
Equation 2.369
where,
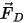 | drag force (N) |
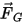 | gravity force (N) |
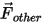 | other forces such as virtual mass force, pressure gradient force, lift force specified by the user (n) |
By default, only the drag force on the particle is considered.
Substituting equation 2.369 into equation 2.366 and dividing it by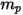 
, the solved force balance equation for a particle has the following form:
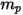, the solved force balance equation for a particle has the following form: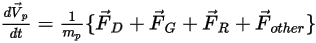
Equation 2.370
To close equation 2.370, you need to calculate the contribution of each individual force. The submodels or formulations adopted in Creo Flow Analysis follow:
◦ Drag Force on Particles
The aerodynamic drag force on a particle is proportional to the phase slip velocity, the difference between the fluid and particle velocities. Assuming that at the same space where the particle is located at a given time, the fluid flow velocity equals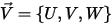 
, you have the drag force expressed as:
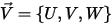, you have the drag force expressed as: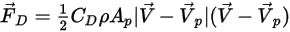
Equation 2.371
where,
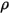 | fluid phase density |
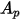 | area of the particle projected in the flow direction |
For a spherical particle with diameter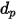 
, 
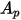is the maximum area of cross section:
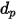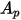, is the maximum area of cross section: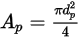
Equation 2.372
is the drag coefficient, which depends on the relative Reynolds number 
:
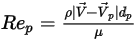
Equation 2.373
where 
is the fluid dynamic viscosity (Pa-s).
is the fluid dynamic viscosity (Pa-s).The drag coefficient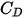 
is introduced to account for experimental results on the viscous drag of a solid sphere. Various models or empirical correlations are developed to determine the drag function 
(
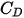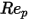) to estimate the fluid-particle exchange. For smooth spherical particles, among many models, the most complete 
function is the corrections by Morsi and Alexander,
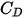is introduced to account for experimental results on the viscous drag of a solid sphere. Various models or empirical correlations are developed to determine the drag function 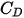(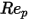) to estimate the fluid-particle exchange. For smooth spherical particles, among many models, the most complete function is the corrections by Morsi and Alexander,References: S. A. Morsi and A. J. Alexander, "An Investigation of Particle Trajectories in Two-Phase Flow Systems", J. Fluid Mech., 55(2) 193–208, September 26 1972.
which has the general expression:
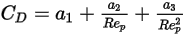
Equation 2.374
where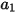 
, 
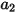, and 
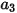are model constants, whose values depend on the relative Reynolds number, as shown in the following table:
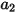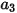, , and are model constants, whose values depend on the relative Reynolds number, as shown in the following table: |  |  |  |
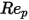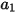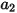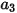0 < 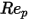 <=0.1 | 0 | 24 | 0 |
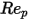0.1 <  <=1 | 3.690 | 22.73 | 0.0903 |
1< 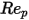 <=10 | 1.222 | 29.1667 | -3.8889 |
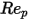10 <  <=100 | 0.6167 | 46.50 | -116.67 |
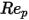100 <  <=1000 | 0.3644 | 98.33 | -2778 |
1000 <  <=5000 | 0.357 | 148.62 | -47500 |
500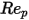0 <  <=10000 | 0.46 | -490.546 | 57870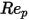0 |
 >10000 | 0.5191 | -1662.5 | 5416700 |
The table shows that at very low particle Reynolds numbers (the viscous regime), 
, the drag coefficient for flow past spherical particles returns to Stokes’ law:
, the drag coefficient for flow past spherical particles returns to Stokes’ law:
Equation 2.375
Conversely, when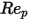 
is sufficiently large so that the inertial effects dominate the viscous effects, the fluid-particle flow is in the inertial or Newton regime. From the table, you observe that the drag coefficient becomes less dependent on the relative Reynolds number. Also, a constant of 
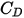value is often used instead of the full Morsi and Alexander model:
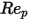is sufficiently large so that the inertial effects dominate the viscous effects, the fluid-particle flow is in the inertial or Newton regime. From the table, you observe that the drag coefficient becomes less dependent on the relative Reynolds number. Also, a constant of 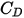value is often used instead of the full Morsi and Alexander model: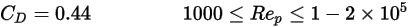
Equation 2.376
In the transitional region between the viscous and inertial regimes, 
, for spherical particles, both viscous and inertial effects are important. Therefore, the drag coefficient is a complex function of the relative Reynolds number, which can be estimated by Morsi and Alexander model or other correlations. For example, according to the Schiller and Naumann model:
, for spherical particles, both viscous and inertial effects are important. Therefore, the drag coefficient is a complex function of the relative Reynolds number, which can be estimated by Morsi and Alexander model or other correlations. For example, according to the Schiller and Naumann model:References: L. Schiller and Z. Naumann, "Z. Ver. Deutsch. Ing. 77. 318. 1935.
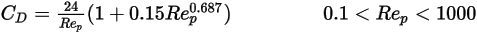
Equation 2.377
To simplify the expression of the drag force term in equation 2.370, the particulate relaxation time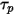 
, is introduced:
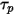, is introduced: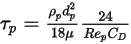
Equation 2.378
If you combine equation 2.368, equation 2.371, equation 2.372, equation 2.373, and equation 2.378, the drag force per unit particle mass has the formulation:
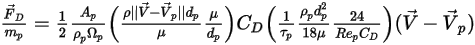
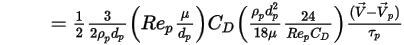
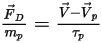
Equation 2.379
Therefore, the default (only the drag force is considered) particle force balance equation is expressed as:
Equation 2.380
• Inclusion of the Gravity Term
By default, the gravity term is not included in the particle force balance equation. You can activate the gravity term in Creo Flow Analysis. For a particle immersed in fluid flow, the effect of gravity results in a buoyancy force which is equal to the weight of the displaced fluid by the particle. Assuming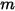 
is the fluid mass displaced by the particle and 
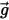is the gravity vector, the resulting force follows as:
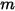is the fluid mass displaced by the particle and 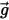is the gravity vector, the resulting force follows as:
Equation 2.381
Or the force per unit particle mass is given as:
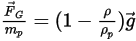
Equation 2.382
And the force balance equation has the form:
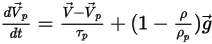
Equation 2.383
• Rotation Force on Particles
For model fluid flows in a rotating reference frame, the rotation-induced additional force term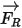 
is an intrinsic part of the particle acceleration. It consists of the effect of the Coriolis and centripetal forces:
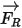is an intrinsic part of the particle acceleration. It consists of the effect of the Coriolis and centripetal forces: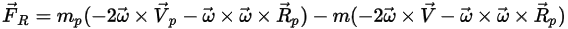
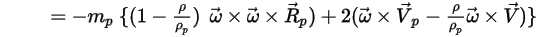
Equation 2.384
Or the rotation force per unit particle mass is given as:
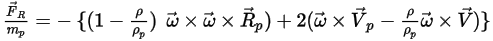
Equation 2.385
where,
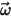 | angular velocity of the rotating reference frame |
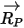 | vector connecting the axis center and particle location |
With the addition of this force term, the particle balance equation is:
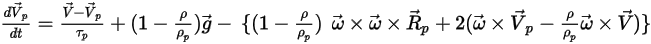
Equation 2.386
Equation 2.386 governs the motion of a particle in a Lagrange system when the flow is solved in a rotating reference frame.
Boundary and Initial Conditions for Particles
In the Lagrange approach, particle tracking is a transient procedure. Therefore, you require the boundary and initial conditions to calculate the trajectories of the particles. Boundary conditions define the particle reaction at the boundaries of the computational domain, particularly of the particle-wall interactions. The initial conditions determine the particle release from boundaries including the release position, frequency, velocity, particle type and size (radius), and the number of particles.
Boundary Conditions
Creo Flow Analysis supplies a discrete phase boundary condition to determine the reaction of particles at a boundary. When a particle reaches a boundary of the flow domain (including physical boundary and solid-fluid interface), for example a wall or an inlet boundary, one of the following occurs:
• Particle reflects through an elastic or inelastic collision.
• Particle escapes through the boundary and is lost from the calculation at the point of impact with the boundary.
• Particle is trapped at the wall and is lost from the calculation at the point of impact with the boundary.
• Particle passes through an internal boundary zone, such as fan or porous jump.
• Particle-boundary interaction is determined by user-defined methods to model the particle reaction when it hits the boundary.
Based on the particle reaction at boundaries, the flow boundary conditions and interfaces are regrouped into three types of discrete particle boundary conditions: Open, Symmetry and Wall.
• Open Discrete Particle Boundary
Particles or streamlines can exit the computational domain. An open boundary is an inlet or outlet boundary of the fluid flow phase in the Euler system. It can also apply to flow boundaries such as wall and symmetry. At an open particle boundary, the particle exits or enters the domain depending on the particle velocity direction.
Let 
be the unit normal vector to the open boundary which points in the direction away from the computational domain, with the particle boundary velocity 
. If 
, the velocity vector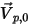 
points away from the computational domain. This indicates that the particle escapes through the boundary and is lost from the calculation at the point of impact with the boundary.
be the unit normal vector to the open boundary which points in the direction away from the computational domain, with the particle boundary velocity . If , the velocity vector 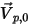points away from the computational domain. This indicates that the particle escapes through the boundary and is lost from the calculation at the point of impact with the boundary.• Symmetry Particle Boundary
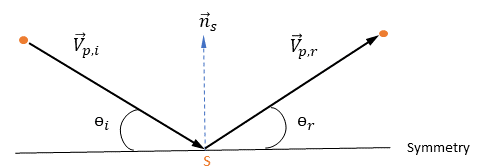
When a particle or streakline in the computational domain hits a discrete symmetry boundary, the boundary condition reflects it back into the domain. For the discrete particle phase, a symmetry particle boundary typically corresponds to a flow symmetry in the Euler system. It can also be a location for particle release.
Let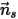 
be the normal-to-symmetry unit vector at point 
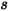of the symmetry, with its direction pointing away from the symmetry to the computational domain. 
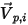and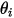 
are introduced to indicate the particle impact velocity angle at the particle symmetry boundary, as shown in the following figure. As the particle reflects from the symmetry, its total kinetic energy is conserved: the tangential velocity remains the same while the normal velocity component only changes the sign. The particle symmetry boundary condition is expressed as:
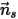be the normal-to-symmetry unit vector at point 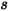of the symmetry, with its direction pointing away from the symmetry to the computational domain. 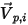and 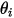are introduced to indicate the particle impact velocity angle at the particle symmetry boundary, as shown in the following figure. As the particle reflects from the symmetry, its total kinetic energy is conserved: the tangential velocity remains the same while the normal velocity component only changes the sign. The particle symmetry boundary condition is expressed as: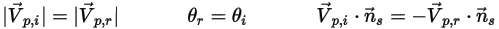
Equation 2.387
where,
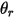 | angle at the point 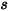 : of the symmetry (deg) |
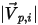 | magnitude of particle incident velocity (m/s) |
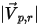 | magnitude of particle reflected velocity (m/s) |
• Wall Particle Boundary
For liquid droplets, the droplet-wall interaction depends on wall temperature, wall material and roughness, impact angle and impact velocity, existence of a wall film, and various other parameters. As a result, a range of submodels are used to reproduce the different regimes of wall-particle interactions and account for the impacts of flow parameters and wall boundary conditions.
In the current discrete particle model, you assume the shape, size, and mass of the particles remain unchanged. Also, you consider the fluid and particles are in thermal equilibrium. Therefore, a simple approach describes the process of particles (has mass) colliding with walls: during the collision process, particles exchange momentum only with the wall, and the particles have one of three ways to interact with the wall. The three ways are perfect bounce, stick bounce, and partial bounce.
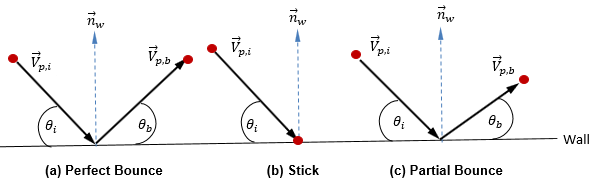
◦ Perfect Bounce—A particle or streakline reflects when it hits a wall. The momentum and kinetic energy of the particle is perfectly conserved. The angle of incidence equals the angle of reflection, while the wall normal velocity component changes sign:
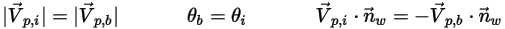
Equation 2.388
where,
 | wall normal unit vector |
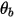 | angle at the wall boundary (deg) |
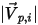 | magnitude of the particle incident velocity (m/s) |
 | magnitude of the particle bounce velocity (m/s) |
◦ Stick—A particle collides with the wall, loses all its momentum and energy, and sticks to the wall:
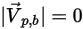
Without the consideration of the particle accumulation along the wall, the particle is then completely lost from the calculation at the point of impact with the boundary.
◦ Partial Bounce—Wall particle condition between the perfect bounce and stick. A particle or streakline bounces from a wall but loses part of the energy in a normal, tangential, or both a normal and tangential direction. Momentum and kinetic energy of the particle is not conserved, and the angle of incidence is usually larger than the angle of reflection:
The loss of energy through particle-wall interaction is specified by user-inputs:
▪ Normal Energy Loss—Specifies loss of the normal component of kinetic energy of a particle on the wall.
▪ Tangential Energy Loss—Specifies loss of the tangential component of kinetic energy of a particle on the wall.
In Creo Flow Analysis, whether a particle bounces, or sticks is determined by the specified values of the maximum and minimum normal velocities. Assuming that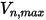 
is the specified particle maximum normal velocity and 
is the specified particle minimum normal velocity, you have the following conditions:
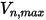is the specified particle maximum normal velocity and is the specified particle minimum normal velocity, you have the following conditions:▪ If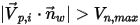 
or 
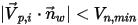, the particle bounces from the wall.
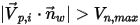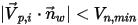or , the particle bounces from the wall.▪ If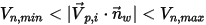 
, the particle sticks to the wall.
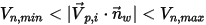, the particle sticks to the wall.Particle-wall interaction models only apply for the particles set to Has Mass. A massless particle follows the flow streamline along the walls.
Note that the particle wall boundaries can be external walls and fluid-solid interfaces. As in the open and symmetry particle boundaries, particles can be released from a wall boundary.
Initial Conditions (Release Particles)
The initial conditions provide the starting values for all dependent discrete phase variables that describe the instantaneous conditions of an individual particle. For the Lagrange system particle tracking, the procedure to determine initial conditions involves particle releases (frequency and distributions) from boundaries (open, symmetry, wall and interface), and assigning properties for each particle.
When you activate Release Particle, the following parameters or variables are the initial conditions for the particle motions:
Integration of Particle Equation of Motion
To track the particle motion, the trajectory equations of each particle are solved (integrated) analytically or numerically in a Lagrange system. From equation 2.367 and equation 2.386, the motion equations are rewritten as:
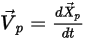
Equation 2.391
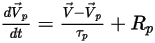
Equation 2.392
where,
 | position vector of the particle |
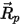 | includes accelerations due to all other forces except drag force such as gravity, rotation effects, and so on |
Equation 2.391 and equation 2.392 are a set of coupled ordinary differential equations. With given initial and boundary conditions, the particle displacement, equation 2.391, is calculated using the forward Euler integration of the particle velocity over time-step,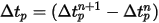 
:
:
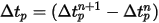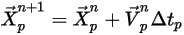
Equation 2.393
where,
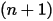 | new values |
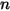 | current values |
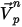 | particle velocity at the current time-step |
At the first time-step,
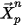 | release position |
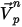| initial velocity |
where,
Equation 2.394
In this forward integration method, the particle velocity calculated at the start of the time-step is assumed to prevail over the entire step. At the end of the time-step, the new particle velocity is calculated by solving the particle momentum equation 2.392. Assuming that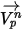 
, 
, and 
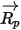are constant over time period 
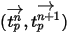, and the fluid properties are taken from the start of the time-step at the time 
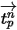, you have the analytical solution of equation 2.392:
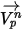, , and 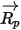are constant over time period 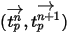, and the fluid properties are taken from the start of the time-step at the time 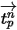, you have the analytical solution of equation 2.392: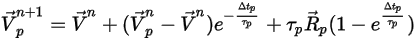
Equation 2.395
To evaluate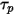 
and 
, you require fluid variables such as density, viscosity, and velocity at the position of the particle. They are considered cell values of the fluid flow phase in which the particle is currently located. Although this analytic scheme is efficient, it can become inaccurate for large time steps and in situations where the particles are not in hydrodynamic equilibrium with the continuous fluid flow. In such a case, the numerical schemes integrate equation 2.392.
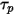and , you require fluid variables such as density, viscosity, and velocity at the position of the particle. They are considered cell values of the fluid flow phase in which the particle is currently located. Although this analytic scheme is efficient, it can become inaccurate for large time steps and in situations where the particles are not in hydrodynamic equilibrium with the continuous fluid flow. In such a case, the numerical schemes integrate equation 2.392.Particle-Fluid Coupling
In the Euler-Lagrange approach, you assume the continuous fluid flow affects particle reaction through forces, heat, and mass transfer. For example, the force term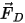 
in the particle force balance equation 2.370 concerns the aerodynamic drag force of flow on the particle. Though the particle phase is considered discrete and does not displace the fluid in volume, the particles can exert a counteracting influence on the fluid flow through the exchanges of momentum, and possibly mass and heat. The effect of the particles on the flow is referred to as particle-fluid coupling. It has two categories:
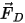in the particle force balance equation 2.370 concerns the aerodynamic drag force of flow on the particle. Though the particle phase is considered discrete and does not displace the fluid in volume, the particles can exert a counteracting influence on the fluid flow through the exchanges of momentum, and possibly mass and heat. The effect of the particles on the flow is referred to as particle-fluid coupling. It has two categories:• One-Way Coupling
One-way coupling allows the fluid to influence trajectories of particles, but particles do not have any effect on the fluid. For massless particles, the particle-fluid interaction is one-way coupling: the particles move along with the fluid flow. For particles that have mass, one-way coupling may be an acceptable approximation in flows with low dispersed phase loadings where particles have a negligible influence on the fluid flow.
For the continuous fluid phase, the flow field is calculated as a single-phase fluid flow without the existence of dispersed particle phase. The particle motion is then tracked based on the computed flow filed and the initial conditions. For a steady-state flow, the particle-tracking occurs after the converged flow solution of the continuous phase is obtained by solving the continuity and Navier-Stokes equations. For a transient flow simulation, the particle motions are tracked at the end of each time-step of the flow simulation.
• Two-Way Coupling
For particles with mass, two-way coupling allows the fluid to influence trajectories of particles. It also accounts for the effect of particles on the continuous fluid phase. Without the inclusion of the mass and heat transfer, the two-way interaction between the fluid and particles only concerns the momentum exchange. For the momentum transferred from the continuous phase to the discrete phase, it is computed by tracking the momentum gained or lost by each individual particle as they pass through a control volume. In two-way coupling, the particle-fluid momentum exchanges are required to be included in the fluid momentum equations to account for the effect of the discrete phase trajectories on the continuum. From equation 2.386, only the drag force accounts for the particle-fluid momentum exchange and is added in the momentum equations. Note that for massless particles, no interchange terms are computed between the fluid flow and them, so that the discrete phase trajectories have no impact on the continuum.
To include the particle-fluid drag effects in the continuous phase momentum equations, the drag force for each particle moving through the flow is applied in the control volume where the particle is located during the time-step. For the particle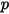 
, you calculate its momentum source due to drag 
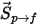from the following differential equation:
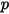, you calculate its momentum source due to drag 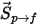from the following differential equation:
Equation 2.396
And the particle source to the continuous phase is the source term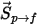 
that you multiply by the number flow rate for that particle (the mass flow rate divided by the mass of the particle):
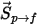that you multiply by the number flow rate for that particle (the mass flow rate divided by the mass of the particle):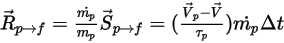
Equation 2.397
where,
 | time-step |
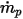 | particle mass flow rate |
Assuming that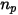 
is the number of particles passing through a control volume at the time-step 
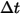, you have the total particle-to-fluid source term:
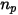is the number of particles passing through a control volume at the time-step 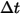, you have the total particle-to-fluid source term: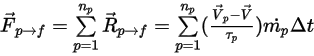
Equation 2.398
With the addition of the fluid-particle drag force, the governing equations solved for the continuous phase are now expressed as:
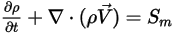
Equation 2.399
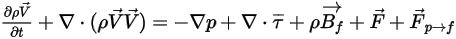
Equation 2.400
With one-way coupling,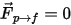 
the continuous fluid phase is governed by the exact single-phase continuity and momentum equations. For two-way coupling, you have the additional particle-to-fluid drag force source term. Equation 2.399 and equation 2.400 are solved identical to the single-phase flow.
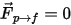the continuous fluid phase is governed by the exact single-phase continuity and momentum equations. For two-way coupling, you have the additional particle-to-fluid drag force source term. Equation 2.399 and equation 2.400 are solved identical to the single-phase flow.