Characteristics of Thermal Radiation
Characteristics of thermal radiation depend on the following properties of the emitting object or body:
• Surface temperature
• Smoothness or roughness of the surface
• Spectral absorptivity
• Spectral emissive power
As electromagnetic waves, thermal radiation comprises of a continuous dispersion of photon energies with a spectrum of frequencies or wavelengths. For an emitting body, the distribution of the spectrum, the peak value of the wavelength, and the total radiated amount of all wavelengths vary with the surface temperature of the emitting body. In turn, at a given surface temperature, the absorptivity, reflectivity and emissivity of the emitting body are all dependent upon the wavelength of the radiation.
Interchange of Radiative Energy
All bodies radiate energy in the form of photons that move in a random direction, with random phase and frequency. When radiated photons from the surface of one body reach the surface of another body, shown in figure 2.35, they may be absorbed, reflected and/or transmitted. The behavior of a surface with radiation incident upon it can be described by the following quantities.
References: R. Siegel and J. R. Howell, “Thermal Radiation Heat Transfer”, Hemisphere Publishing Corporation, Washington DC, 1992.
• Absorptance α—Fraction of incident radiation absorbed at a given wavelength.
• Reflectance ρ—Fraction of incident radiation reflected at a given wavelength.
• Transmittance τ—Fraction of incident radiation transmitted at a given wavelength.
The three coefficients are functions of the wavelength of the electromagnetic waves in radiation λ. From the energy considerations, they must sum to unity:
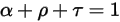
equation 2.273
According to the Kirchhoff’s law of thermal radiation, the emissivity of an emitting body is equal to the spectral absorptivity for any particular wavelength due to reciprocity:
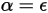
equation 2.274
where ε is the emissivity, the ratio of the radiated energy from an emitting body to that from a perfect emitter (black-body) under the same temperature and wavelength.
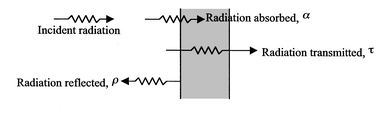
Figure 2.35
Equation 2.273 indicates that the way a body reacts's behavior with regard to thermal radiation is characterized by its absorption α, reflection ρ, and transmission τ. Depending on the values of α,ρ, and τ, the following idealized types of the emitting body are defined:
R. Siegel and J. R. Howell, “Thermal Radiation Heat Transfer”, Hemisphere Publishing Corporation, Washington DC, 1992
• Opaque Body—Does not transmit any radiation that reaches it, but can reflect some radiation. τ=0 and α+ρ=1
• Transparent Body—Transmits all the radiation that reaches it. τ=1 and α=ρ=0
• Black-Body—Theoretical model proposed by Planck. Black-body is an object that absorbs all incident electromagnetic radiation at all wavelengths, regardless of frequency or angle of incidence. If a radiation-emitting object meets the physical characteristics of a black-body in thermodynamic equilibrium, the radiation is called black-body radiation. For a black-body, α=ε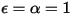 , and
, and 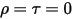
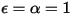 , and
, and 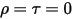
• White Body—Assumed to reflect all incident rays completely and uniformly in all directions. 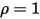 and
and 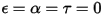
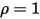 and
and 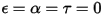
• Gray Body—A body for which 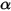 and
and 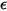 are temperature and wavelength-independent.
are temperature and wavelength-independent.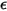 is uniform for all wavelengths. Radiation from a gray body or surface is called gray radiation. Unlike gray radiation, thermal radiation with a spectrum of wavelengths is referred to as nongray radiation.
is uniform for all wavelengths. Radiation from a gray body or surface is called gray radiation. Unlike gray radiation, thermal radiation with a spectrum of wavelengths is referred to as nongray radiation.
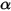 and
and 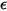 are temperature and wavelength-independent.
are temperature and wavelength-independent.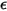 is uniform for all wavelengths. Radiation from a gray body or surface is called gray radiation. Unlike gray radiation, thermal radiation with a spectrum of wavelengths is referred to as nongray radiation.
is uniform for all wavelengths. Radiation from a gray body or surface is called gray radiation. Unlike gray radiation, thermal radiation with a spectrum of wavelengths is referred to as nongray radiation.Radiative Power
• Power 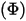 —Total or net radiative energy emitted, reflected, transmitted, or received per unit time for a given source.
—Total or net radiative energy emitted, reflected, transmitted, or received per unit time for a given source.
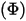 —Total or net radiative energy emitted, reflected, transmitted, or received per unit time for a given source.
—Total or net radiative energy emitted, reflected, transmitted, or received per unit time for a given source.• Irradiance (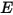 )—Radiation power received by a surface
)—Radiation power received by a surface 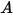 per unit area.
per unit area. 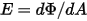
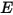 )—Radiation power received by a surface
)—Radiation power received by a surface 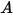 per unit area.
per unit area. 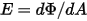
• Emittance (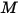 )—Radiation power emitted
)—Radiation power emitted 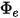 by a surface per unit area.
by a surface per unit area. 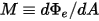
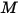 )—Radiation power emitted
)—Radiation power emitted 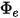 by a surface per unit area.
by a surface per unit area. 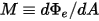
• Intensity (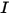 )—Power radiated in a given direction (solid angle
)—Power radiated in a given direction (solid angle  ), for a given source.
), for a given source. 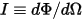
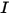 )—Power radiated in a given direction (solid angle
)—Power radiated in a given direction (solid angle  ), for a given source.
), for a given source. 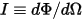
• Radiance (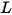 )—Radiant power emitted, reflected, transmitted, or received by a given surface, per unit solid angle per unit projected area.
)—Radiant power emitted, reflected, transmitted, or received by a given surface, per unit solid angle per unit projected area. 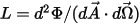
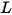 )—Radiant power emitted, reflected, transmitted, or received by a given surface, per unit solid angle per unit projected area.
)—Radiant power emitted, reflected, transmitted, or received by a given surface, per unit solid angle per unit projected area. 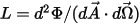
• Planck's Law
Thermal radiation emitted by a body at any temperature consists of a wide range of frequencies. For a black-body, Planck's law describes the frequency distribution of the black-body radiation as only the function of the object’s temperature. Planck showed that the spectral radiance of a black-body, 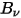 , defined as the power emitted per unit area of the body, per unit solid angle that the radiation is measured over, and per unit frequency,
, defined as the power emitted per unit area of the body, per unit solid angle that the radiation is measured over, and per unit frequency, 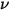 , has the formulation respective to the body temperature:
, has the formulation respective to the body temperature:
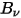 , defined as the power emitted per unit area of the body, per unit solid angle that the radiation is measured over, and per unit frequency,
, defined as the power emitted per unit area of the body, per unit solid angle that the radiation is measured over, and per unit frequency, 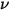 , has the formulation respective to the body temperature:
, has the formulation respective to the body temperature: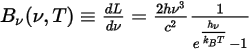
Equation 2.275
where,
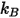 | Boltzmann constant |
h | Planck constant |
c | speed of light in vacuum or material medium |
The spectral radiance is also expressed per unit wavelength, λ:
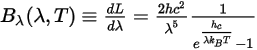
Equation 2.276
• Stefan-Boltzmann’s Law:
Through the integration of Planck’s law over frequency, v, the power output given by Stefan-Boltzmann’s law is the power emitted from a black-body in terms of its temperature. Stefan-Boltzmann’s law is also known as the black-body radiant emittance. Stefan-Boltzmann’s law states that the total energy radiated per unit surface area of a black-body across all wavelengths per unit time, is directly proportional to the fourth power of the black-body's thermodynamic temperature. 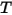 :
:
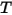 :
: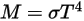
2.277
where,
σ | Stefan-Boltzmann constant |
M | radiant emittance |
For a gray-body, which does not absorb all incident radiation, emits less total energy than a black-body. With the introduction of the emissivity,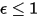 (black-body:
(black-body: 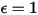 ), equation 2.277 is extended to a gray-body:
), equation 2.277 is extended to a gray-body:
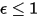 (black-body:
(black-body: 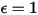 ), equation 2.277 is extended to a gray-body:
), equation 2.277 is extended to a gray-body: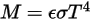
2.278
From Stefan-Boltzmann’s law, the radiance and power emitted by a body are calculated as:
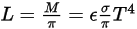
equation 2.279
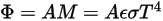
Equation 2.280
• Wien’s Displacement Law
Wien’s displacement law states that the wavelength λ, for which the spectral radiance of a black-body radiation per unit wavelength reaches its peak value, is inversely proportional to the temperature:
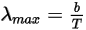
Equation 2.281
where b is Wien’s displacement constant.
Model Constants
The model constants used in the above theoretical models are in the following table:
h | Planck’s constant | 6.626 069 3(11) ×10-34J-s = 4.135 667 43(35) ×10-15eV-s |
b | Wien’s displacement constant | 2.897 768 5(51) ×10-3m-K |
kB | Boltzmann constant | 1.380 650 5(24) ×10-23J/K = 8.617 343 (15) ×10-5eV/K |
σ | Stefan-Boltzmann constant | 5.670 373 (21) ×10-8 W/(m2-K4) |
c | Speed of light | 299 792 458 m/s |