Solver EDO
Las ecuaciones diferenciales ordinarias (EDO), la ecuación 2.432 y la ecuación 2.444, que gobiernan la traslación y rotación 1-GDL de los límites y volúmenes respectivamente, se resuelven de forma numérica en Creo Flow Analysis. Concretamente, para calcular un movimiento de límite y volumen y un desplazamiento para la redefinición de malla, se adoptan los siguientes esquemas de paso de tiempo para integrar las ecuaciones EDO: solver explícito de adherencia, Euler y Runge-Kutta.
Integración de una ecuación de traslación de un GDL
Si se sustituyen la ecuación 2.434, la ecuación 2.435, la ecuación 2.436 en la ecuación 2.432 y se agrupan los términos explícitos de fuerza en un único término, 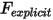 para brevedad, se vuelve a escribir la ecuación de traslación 1-GDL de la siguiente forma:
para brevedad, se vuelve a escribir la ecuación de traslación 1-GDL de la siguiente forma:
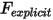 para brevedad, se vuelve a escribir la ecuación de traslación 1-GDL de la siguiente forma:
para brevedad, se vuelve a escribir la ecuación de traslación 1-GDL de la siguiente forma: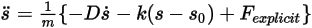
Ecuación 2.455
donde el término de fuerza calculado explícitamente 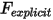 es:
es:
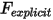 es:
es: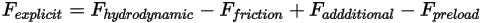
Ecuación 2.456
Con las condiciones iniciales y de límite dadas, el desplazamiento del cuerpo sólido se obtiene al integrar la ecuación 2.455 mediante esquemas de paso de tiempo explícitos. Con el paso del tiempo 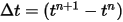 , se disponen de formulaciones generales de la siguiente manera:
, se disponen de formulaciones generales de la siguiente manera:
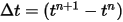 , se disponen de formulaciones generales de la siguiente manera:
, se disponen de formulaciones generales de la siguiente manera: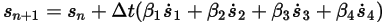
Ecuación 2.457
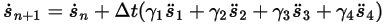
Ecuación 2.458
donde los factores de ponderación suman la unidad:
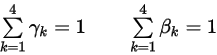
Ecuación 2.459
Con la elección de factores de ponderación, se derivan distintos esquemas. Por ejemplo, los esquemas explícitos de Euler y Runge-Kutta son los siguientes:
• Solver explícito de Euler (1er orden)
Con 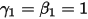 y
y 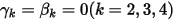 , se dispone del esquema explícito de Euler en lo siguiente:
, se dispone del esquema explícito de Euler en lo siguiente:
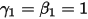 y
y 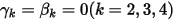 , se dispone del esquema explícito de Euler en lo siguiente:
, se dispone del esquema explícito de Euler en lo siguiente: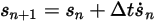
Ecuación 2.460
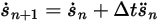
Ecuación 2.461
• Solver explícito de Runge-Kutta
Los solvers de Runge-Kutta son esquemas explícitos de 2o orden y de 4o orden, que son los siguientes:
◦ Esquema de segundo orden
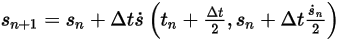
Ecuación 2.462
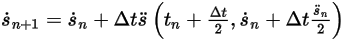
Ecuación 2.463
◦ Esquema de cuarto orden
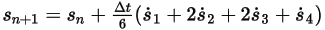
Ecuación 2.464
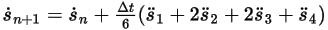
Ecuación 2.465
donde,

Ecuación 2.466

Ecuación 2.467

Ecuación 2.468

Ecuación 2.469
• Solver de adherencia (explícito)
Además de los esquemas estándar de Euler y Runge-Kutta, Creo Flow Analysis ha desarrollado su solver de adherencia para integrar la ecuación de traslación EDO 1-GDL. Es el método por defecto para los movimientos dinámicos de cuerpos sólidos.
Integración de una ecuación de rotación de un GDL
En cuanto a la traslación, mediante la sustitución de la ecuación 2.446 y la ecuación 2.447 en la ecuación 2.444 y la agrupación de los términos de torsión explícitos en un término único 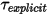 para brevedad, se vuelve a escribir la ecuación de movimiento de rotación 1-GDL, la ecuación 2.444 de la forma siguiente:
para brevedad, se vuelve a escribir la ecuación de movimiento de rotación 1-GDL, la ecuación 2.444 de la forma siguiente:
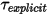 para brevedad, se vuelve a escribir la ecuación de movimiento de rotación 1-GDL, la ecuación 2.444 de la forma siguiente:
para brevedad, se vuelve a escribir la ecuación de movimiento de rotación 1-GDL, la ecuación 2.444 de la forma siguiente: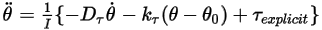
Ecuación 2.470
donde el término de torsión que se calcula explícitamente  es:
es:
 es:
es: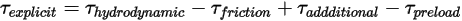
Ecuación 2.471
Con las condiciones iniciales y de límite dadas, el ángulo de rotación se obtiene al integrar la ecuación 2.470 mediante esquemas de paso de tiempo explícitos. Con el paso del tiempo 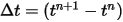 , se disponen de formulaciones generales de la siguiente manera:
, se disponen de formulaciones generales de la siguiente manera:
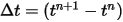 , se disponen de formulaciones generales de la siguiente manera:
, se disponen de formulaciones generales de la siguiente manera: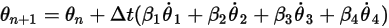
Ecuación 2.472
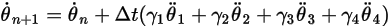
Ecuación 2.473
donde los factores de ponderación suman la unidad:
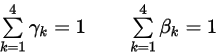
Ecuación 2.474
Con la elección de factores de ponderación, se derivan fácilmente diferentes esquemas numéricos. De nuevo, los esquemas explícitos de Euler y Runge-Kutta se indican a continuación:
• Solver explícito de Euler (1er orden)
Con 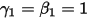 y
y 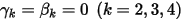 , se dispone del esquema explícito de Euler en lo siguiente:
, se dispone del esquema explícito de Euler en lo siguiente:
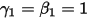 y
y 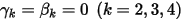 , se dispone del esquema explícito de Euler en lo siguiente:
, se dispone del esquema explícito de Euler en lo siguiente: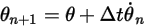
Ecuación 2.475
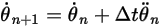
Ecuación 2.476
• Solver explícito de Runge-Kutta
Los solvers de Runge-Kutta son esquemas explícitos de 2o orden y de 4o orden, que son los siguientes:
◦ Esquema de segundo orden
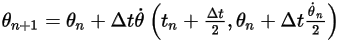
Ecuación 2.477
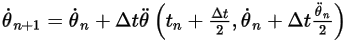
Ecuación 2.478
◦ Esquema de cuarto orden
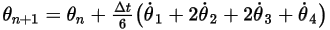
Ecuación 2.479
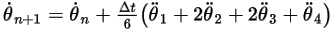
Ecuación 2.480
donde,

Ecuación 2.481

Ecuación 2.482

Ecuación 2.483

Ecuación 2.484
• Solver de adherencia (explícito)
Además de los esquemas estándar de Euler y Runge-Kutta, Creo Flow Analysis ha desarrollado su solver de adherencia para integrar la ecuación 2.444 ODE de rotación 1-GDL. Es el método por defecto para los movimientos dinámicos de cuerpos sólidos.