Movimientos de un cuerpo rígido
En las simulaciones, las superficies de un objeto sólido suelen ser límites de pared en un dominio de flujo. Cuando un objeto sólido o una superficie se somete a fuerzas dinámicas y mecánicas, así como al efecto térmico, el desequilibrio de las fuerzas netas puede hacer que el cuerpo se mueva y deforme. En las simulaciones de flujo, un objeto sólido se considera a menudo como un cuerpo rígido. Por lo tanto, para un objeto sólido sujeto a desequilibrios de fuerzas, se supone que se puede mover de forma lineal (traslación), angular (rotación) o ambas lineal y angular, sin deformación. Sin embargo, en el caso de un dominio computacional CFA, el movimiento de límite puede dar lugar al cambio de dominio y, por consiguiente, la malla de volumen se puede deformar, tal como se describe en el módulo Flujo (Flow).
En el caso de un cuerpo rígido, las ecuaciones que gobiernan sus movimientos se derivan directamente de la conservación del momento lineal y angular:
• Momento lineal (traslación)
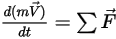
Ecuación 2.426
• Momento angular (rotación)
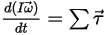
Ecuación 2.427
En la ecuación 2.426, 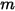 es la masa del objeto en movimiento;
es la masa del objeto en movimiento; 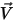 ⃗ es la velocidad lineal/de transición; y
⃗ es la velocidad lineal/de transición; y 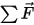 ⃗ corresponde a las fuerzas totales/netas ejercidas en el cuerpo bajo traslación. En la ecuación 2.427,
⃗ corresponde a las fuerzas totales/netas ejercidas en el cuerpo bajo traslación. En la ecuación 2.427, 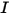 es el momento de inercia;
es el momento de inercia; 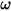 ⃗ es la velocidad angular y
⃗ es la velocidad angular y 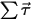 ⃗ es la torsión total/neta que se aplica en el cuerpo rotatorio.
⃗ es la torsión total/neta que se aplica en el cuerpo rotatorio.
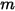 es la masa del objeto en movimiento;
es la masa del objeto en movimiento; 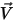 ⃗ es la velocidad lineal/de transición; y
⃗ es la velocidad lineal/de transición; y 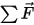 ⃗ corresponde a las fuerzas totales/netas ejercidas en el cuerpo bajo traslación. En la ecuación 2.427,
⃗ corresponde a las fuerzas totales/netas ejercidas en el cuerpo bajo traslación. En la ecuación 2.427, 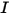 es el momento de inercia;
es el momento de inercia; 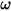 ⃗ es la velocidad angular y
⃗ es la velocidad angular y 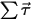 ⃗ es la torsión total/neta que se aplica en el cuerpo rotatorio.
⃗ es la torsión total/neta que se aplica en el cuerpo rotatorio.La ecuación 2.426 y la ecuación 2.427 gobiernan los movimientos generales de un cuerpo sólido, que tienen seis grados de libertad de movimiento (6-GDL) con tres grados para la traslación (3-GDL) y otros tres para la rotación (3-GDL). En Creo Flow Analysis, solo se tienen en cuenta la traslación y la rotación 1-GDL, que se explican en esta sección.
Traslación de un GDL
Suponiendo que un cuerpo sólido se mueva de forma lineal en una dirección especificada arbitrariamente (permanece sin cambios), definida por un vector de unidad 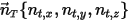 , el movimiento de traslación del cuerpo se reduce a un grado de libertad (1-GDL). Como resultado, para la conservación de momento lineal, la ecuación 2.426 se convierte en una ecuación escalar a lo largo de la dirección del movimiento, ya que la velocidad del movimiento y la fuerza se expresan en términos de
, el movimiento de traslación del cuerpo se reduce a un grado de libertad (1-GDL). Como resultado, para la conservación de momento lineal, la ecuación 2.426 se convierte en una ecuación escalar a lo largo de la dirección del movimiento, ya que la velocidad del movimiento y la fuerza se expresan en términos de 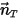 :
:
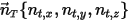 , el movimiento de traslación del cuerpo se reduce a un grado de libertad (1-GDL). Como resultado, para la conservación de momento lineal, la ecuación 2.426 se convierte en una ecuación escalar a lo largo de la dirección del movimiento, ya que la velocidad del movimiento y la fuerza se expresan en términos de
, el movimiento de traslación del cuerpo se reduce a un grado de libertad (1-GDL). Como resultado, para la conservación de momento lineal, la ecuación 2.426 se convierte en una ecuación escalar a lo largo de la dirección del movimiento, ya que la velocidad del movimiento y la fuerza se expresan en términos de 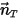 :
: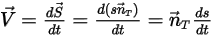
Ecuación 2.428
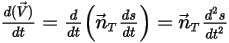
Ecuación 2.429
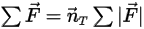
Ecuación 2.430
donde 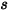 es la magnitud del vector de posición
es la magnitud del vector de posición 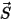 en un punto de interés del cuerpo sólido a lo largo de la dirección del movimiento
en un punto de interés del cuerpo sólido a lo largo de la dirección del movimiento 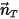 . En un sistema de coordenadas cartesiano, se encuentra lo siguiente
. En un sistema de coordenadas cartesiano, se encuentra lo siguiente
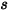 es la magnitud del vector de posición
es la magnitud del vector de posición 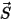 en un punto de interés del cuerpo sólido a lo largo de la dirección del movimiento
en un punto de interés del cuerpo sólido a lo largo de la dirección del movimiento 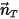 . En un sistema de coordenadas cartesiano, se encuentra lo siguiente
. En un sistema de coordenadas cartesiano, se encuentra lo siguiente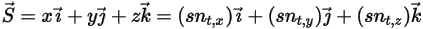
Ecuación 2.431
Si la masa del cuerpo sólido permanece constante y se expande el término de fuerza para incluir explícitamente todas las fuerzas aplicadas en el cuerpo, se tiene la ecuación de momento lineal escalar:
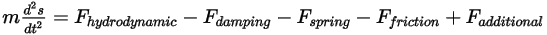
Ecuación 2.432
Las fuerzas del lado derecho indican lo siguiente:
• Fuerza hidrodinámica  : se compone de fuerzas de presión y de corte. Se producen por el movimiento relativo entre el flujo de fluido y las superficies del cuerpo sólido que están en contacto con el flujo. Las fuerzas de presión y corte se obtienen de las soluciones de flujo (cantidades de salida):
: se compone de fuerzas de presión y de corte. Se producen por el movimiento relativo entre el flujo de fluido y las superficies del cuerpo sólido que están en contacto con el flujo. Las fuerzas de presión y corte se obtienen de las soluciones de flujo (cantidades de salida):
 : se compone de fuerzas de presión y de corte. Se producen por el movimiento relativo entre el flujo de fluido y las superficies del cuerpo sólido que están en contacto con el flujo. Las fuerzas de presión y corte se obtienen de las soluciones de flujo (cantidades de salida):
: se compone de fuerzas de presión y de corte. Se producen por el movimiento relativo entre el flujo de fluido y las superficies del cuerpo sólido que están en contacto con el flujo. Las fuerzas de presión y corte se obtienen de las soluciones de flujo (cantidades de salida):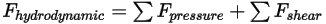
Ecuación 2.433
• Fuerza de amortiguación 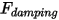 : una fuerza de retardo causada por el efecto de amortiguación por fricción. Se determina por el movimiento del objeto sólido y el coeficiente de amortiguación definido por el usuario
: una fuerza de retardo causada por el efecto de amortiguación por fricción. Se determina por el movimiento del objeto sólido y el coeficiente de amortiguación definido por el usuario 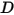 :
:
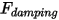 : una fuerza de retardo causada por el efecto de amortiguación por fricción. Se determina por el movimiento del objeto sólido y el coeficiente de amortiguación definido por el usuario
: una fuerza de retardo causada por el efecto de amortiguación por fricción. Se determina por el movimiento del objeto sólido y el coeficiente de amortiguación definido por el usuario 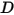 :
: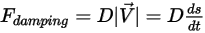
Ecuación 2.434
• Fuerza de muelle 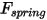 : depende del desplazamiento del muelle
: depende del desplazamiento del muelle 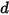 , la constante del muelle
, la constante del muelle 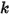 y la fuerza de precarga del muelle
y la fuerza de precarga del muelle 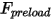 :
:
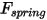 : depende del desplazamiento del muelle
: depende del desplazamiento del muelle 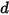 , la constante del muelle
, la constante del muelle 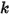 y la fuerza de precarga del muelle
y la fuerza de precarga del muelle 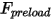 :
: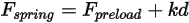
Ecuación 2.435
donde el desplazamiento del muelle 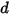 se define como:
se define como:
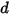 se define como:
se define como: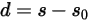
Ecuación 2.436
donde 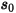 es la magnitud del vector de posición
es la magnitud del vector de posición 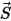 en la ubicación anterior
en la ubicación anterior 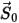 .
.
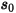 es la magnitud del vector de posición
es la magnitud del vector de posición 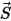 en la ubicación anterior
en la ubicación anterior 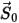 .
.• Fuerza de fricción: se adopta el modelo de fricción por contacto para tener en cuenta el efecto de la fricción en un sistema dinámico. La fuerza de fricción 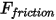 se modela como:
se modela como:
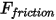 se modela como:
se modela como: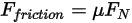
Ecuación 2.437
donde 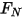 es el componente normal de la fuerza de contacto ejercida sobre la superficie sólida de interés. Para el coeficiente de fricción
es el componente normal de la fuerza de contacto ejercida sobre la superficie sólida de interés. Para el coeficiente de fricción 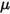 , se introduce además el coeficiente de fricción estática
, se introduce además el coeficiente de fricción estática 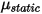 y el coeficiente de fricción deslizante
y el coeficiente de fricción deslizante 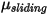 para los cuerpos estacionarios y móviles, respectivamente:
para los cuerpos estacionarios y móviles, respectivamente:
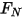 es el componente normal de la fuerza de contacto ejercida sobre la superficie sólida de interés. Para el coeficiente de fricción
es el componente normal de la fuerza de contacto ejercida sobre la superficie sólida de interés. Para el coeficiente de fricción 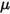 , se introduce además el coeficiente de fricción estática
, se introduce además el coeficiente de fricción estática 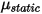 y el coeficiente de fricción deslizante
y el coeficiente de fricción deslizante 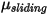 para los cuerpos estacionarios y móviles, respectivamente:
para los cuerpos estacionarios y móviles, respectivamente: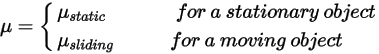
Ecuación 2.438
• Fuerza adicional 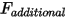 : se añade para fuerzas adicionales especificadas por el usuario.
: se añade para fuerzas adicionales especificadas por el usuario.
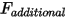 : se añade para fuerzas adicionales especificadas por el usuario.
: se añade para fuerzas adicionales especificadas por el usuario.Rotación de un GDL
Cuando un eje rotatorio arbitrario se define mediante un punto (centro del eje) 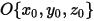 y el vector de unidad direccional
y el vector de unidad direccional 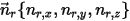 , la rotación del cuerpo sólido alrededor del eje
, la rotación del cuerpo sólido alrededor del eje 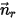 también se reduce a una rotación de 1-GDL. Del mismo modo, para la conservación del momento angular, la ecuación 2.427 también se convierte en una ecuación escalar a lo largo de la dirección tangencial
también se reduce a una rotación de 1-GDL. Del mismo modo, para la conservación del momento angular, la ecuación 2.427 también se convierte en una ecuación escalar a lo largo de la dirección tangencial 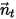 , definida como:
, definida como:
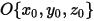 y el vector de unidad direccional
y el vector de unidad direccional 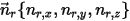 , la rotación del cuerpo sólido alrededor del eje
, la rotación del cuerpo sólido alrededor del eje 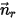 también se reduce a una rotación de 1-GDL. Del mismo modo, para la conservación del momento angular, la ecuación 2.427 también se convierte en una ecuación escalar a lo largo de la dirección tangencial
también se reduce a una rotación de 1-GDL. Del mismo modo, para la conservación del momento angular, la ecuación 2.427 también se convierte en una ecuación escalar a lo largo de la dirección tangencial 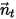 , definida como:
, definida como: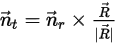
Ecuación 2.439
donde 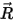 es el vector que apunta desde el centro del eje a un punto arbitrario
es el vector que apunta desde el centro del eje a un punto arbitrario 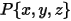 del cuerpo sólido:
del cuerpo sólido:
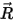 es el vector que apunta desde el centro del eje a un punto arbitrario
es el vector que apunta desde el centro del eje a un punto arbitrario 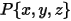 del cuerpo sólido:
del cuerpo sólido: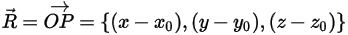
Ecuación 2.440
La velocidad angular y la torsión en el punto 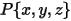 se reformulan como:
se reformulan como:
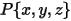 se reformulan como:
se reformulan como: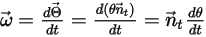
Ecuación 2.441
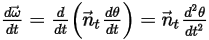
Ecuación 2.442
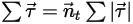
Ecuación 2.443
donde 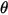 es el ángulo de rotación del punto
es el ángulo de rotación del punto 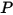 relativo a la ubicación inicial o de referencia.
relativo a la ubicación inicial o de referencia.
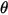 es el ángulo de rotación del punto
es el ángulo de rotación del punto 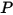 relativo a la ubicación inicial o de referencia.
relativo a la ubicación inicial o de referencia.Si el momento de inercia permanece constante y se expande el término de torsión para incluir explícitamente todas las torsiones aplicadas al cuerpo rotatorio, se dispone de la ecuación de momento angular escalar como:
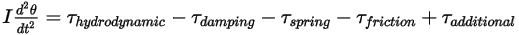
Ecuación 2.444
Los términos de torsión del lado derecho se definen de la siguiente manera:
• Torsión hidrodinámica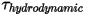 : combinación de torsión debida a las fuerzas de presión y de corte.
: combinación de torsión debida a las fuerzas de presión y de corte.
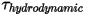 : combinación de torsión debida a las fuerzas de presión y de corte.
: combinación de torsión debida a las fuerzas de presión y de corte.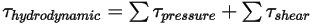
Ecuación 2.445
• Torsión de amortiguación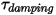 : depende de la velocidad de rotación
: depende de la velocidad de rotación 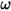 y del coeficiente de amortiguación definido por el usuario,
y del coeficiente de amortiguación definido por el usuario, 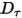 .
.
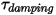 : depende de la velocidad de rotación
: depende de la velocidad de rotación 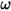 y del coeficiente de amortiguación definido por el usuario,
y del coeficiente de amortiguación definido por el usuario, 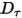 .
.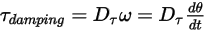
Ecuación 2.446
• Torsión de muelle 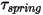 : la torsión inducida por torsión que depende del ángulo de desplazamiento
: la torsión inducida por torsión que depende del ángulo de desplazamiento 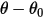 , la torsión precargada definida por el usuario
, la torsión precargada definida por el usuario 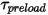 y la constante de torsión
y la constante de torsión 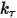 .
.
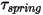 : la torsión inducida por torsión que depende del ángulo de desplazamiento
: la torsión inducida por torsión que depende del ángulo de desplazamiento 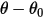 , la torsión precargada definida por el usuario
, la torsión precargada definida por el usuario 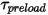 y la constante de torsión
y la constante de torsión 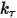 .
.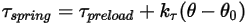
Ecuación 2.447
donde 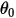 es el ángulo de referencia. Normalmente, se trata de la posición del límite o volumen durante la configuración del modelo, pero puede corresponder a una ubicación diferente. Por ejemplo, en un desplazamiento angular cero, el ángulo de referencia
es el ángulo de referencia. Normalmente, se trata de la posición del límite o volumen durante la configuración del modelo, pero puede corresponder a una ubicación diferente. Por ejemplo, en un desplazamiento angular cero, el ángulo de referencia 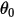 no es el mismo que el de la posición angular inicial.
no es el mismo que el de la posición angular inicial.
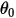 es el ángulo de referencia. Normalmente, se trata de la posición del límite o volumen durante la configuración del modelo, pero puede corresponder a una ubicación diferente. Por ejemplo, en un desplazamiento angular cero, el ángulo de referencia
es el ángulo de referencia. Normalmente, se trata de la posición del límite o volumen durante la configuración del modelo, pero puede corresponder a una ubicación diferente. Por ejemplo, en un desplazamiento angular cero, el ángulo de referencia 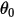 no es el mismo que el de la posición angular inicial.
no es el mismo que el de la posición angular inicial.• Torsión de fricción: torsión causada por la fuerza de fricción que se produce cuando se mueven dos objetos en contacto. En experimentos, se determina por la diferencia entre la torsión aplicada y la torsión observada o de red. Depende del coeficiente de fricción 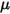 y la torsión de contacto debida a la fuerza normal
y la torsión de contacto debida a la fuerza normal 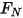 aplicada sobre la superficie de contacto:
aplicada sobre la superficie de contacto:
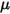 y la torsión de contacto debida a la fuerza normal
y la torsión de contacto debida a la fuerza normal 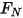 aplicada sobre la superficie de contacto:
aplicada sobre la superficie de contacto: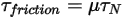
Ecuación 2.448
donde 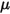 es un parámetro definido por el usuario, definido en la ecuación 2.438.
es un parámetro definido por el usuario, definido en la ecuación 2.438.
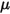 es un parámetro definido por el usuario, definido en la ecuación 2.438.
es un parámetro definido por el usuario, definido en la ecuación 2.438.• Torsiones adicionales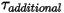 : se añade para las torsiones adicionales especificadas por el usuario.
: se añade para las torsiones adicionales especificadas por el usuario.
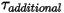 : se añade para las torsiones adicionales especificadas por el usuario.
: se añade para las torsiones adicionales especificadas por el usuario.Modelo de rebote
En muchas situaciones, un cuerpo sólido solo se traslada, gira o se traslada y gira en un espacio limitado (una distancia o ángulo limitados), es decir, que tiene un máximo, un mínimo o bien una posición máxima y una mínima. Por ejemplo, tal como se muestra en la siguiente figura, cuando un péndulo de gravedad simple se libera desde la posición original con el ángulo 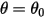 , la fuerza de restauración que actúa sobre su masa provoca que oscile alrededor de la posición de equilibrio. El ángulo máximo en cualquiera de los lados de la posición de equilibrio
, la fuerza de restauración que actúa sobre su masa provoca que oscile alrededor de la posición de equilibrio. El ángulo máximo en cualquiera de los lados de la posición de equilibrio 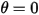 depende de su posición de liberación
depende de su posición de liberación 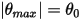 . Si no hay fricción (giro sin fricción y en el vacío), el ángulo máximo permanece sin cambios y el péndulo oscila de un lado a otro permanentemente, con las mismas posiciones extremas. Sin embargo, cuando un péndulo se encuentra en la atmósfera, por ejemplo, la resistencia del aire (amortiguación) hace que el ángulo máximo de oscilación se reduzca con el tiempo y, finalmente, se detenga en la posición de equilibrio.
. Si no hay fricción (giro sin fricción y en el vacío), el ángulo máximo permanece sin cambios y el péndulo oscila de un lado a otro permanentemente, con las mismas posiciones extremas. Sin embargo, cuando un péndulo se encuentra en la atmósfera, por ejemplo, la resistencia del aire (amortiguación) hace que el ángulo máximo de oscilación se reduzca con el tiempo y, finalmente, se detenga en la posición de equilibrio.
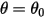 , la fuerza de restauración que actúa sobre su masa provoca que oscile alrededor de la posición de equilibrio. El ángulo máximo en cualquiera de los lados de la posición de equilibrio
, la fuerza de restauración que actúa sobre su masa provoca que oscile alrededor de la posición de equilibrio. El ángulo máximo en cualquiera de los lados de la posición de equilibrio 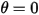 depende de su posición de liberación
depende de su posición de liberación 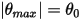 . Si no hay fricción (giro sin fricción y en el vacío), el ángulo máximo permanece sin cambios y el péndulo oscila de un lado a otro permanentemente, con las mismas posiciones extremas. Sin embargo, cuando un péndulo se encuentra en la atmósfera, por ejemplo, la resistencia del aire (amortiguación) hace que el ángulo máximo de oscilación se reduzca con el tiempo y, finalmente, se detenga en la posición de equilibrio.
. Si no hay fricción (giro sin fricción y en el vacío), el ángulo máximo permanece sin cambios y el péndulo oscila de un lado a otro permanentemente, con las mismas posiciones extremas. Sin embargo, cuando un péndulo se encuentra en la atmósfera, por ejemplo, la resistencia del aire (amortiguación) hace que el ángulo máximo de oscilación se reduzca con el tiempo y, finalmente, se detenga en la posición de equilibrio.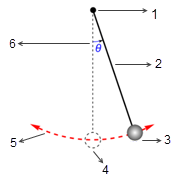
figura
1. Giro sin fricción
2. Varilla sin masa
3. Oscilación masiva
4. Posición de equilibrio
5. Trayectoria de la oscilación
6. Amplitud
Además, en un ciclo de oscilación (período), cuando el péndulo alcanza la posición más alta 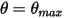 , cambia la dirección con la pérdida total de su energía cinética. En el péndulo de gravedad simple, la energía cinética se transfiere completamente a energía potencial, mientras que cuando se considera la resistencia del medio, se pierde una parte de la energía cinética para superar la amortiguación viscosa. Sin embargo, la fuerza neta o la energía potencial gobierna el péndulo para que empiece a moverse en dirección opuesta hacia la posición de equilibrio, donde la energía cinética (velocidad) es la máxima, mientras que la potencial es la mínima. En este caso,
, cambia la dirección con la pérdida total de su energía cinética. En el péndulo de gravedad simple, la energía cinética se transfiere completamente a energía potencial, mientras que cuando se considera la resistencia del medio, se pierde una parte de la energía cinética para superar la amortiguación viscosa. Sin embargo, la fuerza neta o la energía potencial gobierna el péndulo para que empiece a moverse en dirección opuesta hacia la posición de equilibrio, donde la energía cinética (velocidad) es la máxima, mientras que la potencial es la mínima. En este caso, 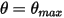 indica una condición de sin rebote para la ecuación 2.444 de momento angular 1-GDL.
indica una condición de sin rebote para la ecuación 2.444 de momento angular 1-GDL.
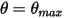 , cambia la dirección con la pérdida total de su energía cinética. En el péndulo de gravedad simple, la energía cinética se transfiere completamente a energía potencial, mientras que cuando se considera la resistencia del medio, se pierde una parte de la energía cinética para superar la amortiguación viscosa. Sin embargo, la fuerza neta o la energía potencial gobierna el péndulo para que empiece a moverse en dirección opuesta hacia la posición de equilibrio, donde la energía cinética (velocidad) es la máxima, mientras que la potencial es la mínima. En este caso,
, cambia la dirección con la pérdida total de su energía cinética. En el péndulo de gravedad simple, la energía cinética se transfiere completamente a energía potencial, mientras que cuando se considera la resistencia del medio, se pierde una parte de la energía cinética para superar la amortiguación viscosa. Sin embargo, la fuerza neta o la energía potencial gobierna el péndulo para que empiece a moverse en dirección opuesta hacia la posición de equilibrio, donde la energía cinética (velocidad) es la máxima, mientras que la potencial es la mínima. En este caso, 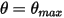 indica una condición de sin rebote para la ecuación 2.444 de momento angular 1-GDL.
indica una condición de sin rebote para la ecuación 2.444 de momento angular 1-GDL.Además de la condición sin rebote, es posible que un cuerpo en movimiento en la posición de limite no pierda ninguna energía cinética y rebote (rebote perfecto) o pierda solo parte de la energía cinética (rebote parcial). Por lo tanto, se aplican las tres condiciones de rebote siguientes cuando se resuelven las ecuaciones de traslación y rotación dinámicas 1-GDL, la ecuación 2.432 y la ecuación 2.444, para determinar los movimientos de un cuerpo sólido o un límite de pared para el dominio de flujo:
• Sin rebote: modelo por defecto de Creo Flow Analysis. Esto determina que cuando un cuerpo sólido o un límite alcanza el límite de su movimiento, cambia la dirección con la pérdida total de su energía cinética. Con 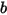 y
y  que representan el rebote y la incidencia, y
que representan el rebote y la incidencia, y 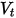 y
y 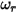 la velocidad de traslación y rotación (solo magnitud), este modelo de rebote se expresa de la siguiente manera:
la velocidad de traslación y rotación (solo magnitud), este modelo de rebote se expresa de la siguiente manera:
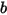 y
y  que representan el rebote y la incidencia, y
que representan el rebote y la incidencia, y 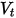 y
y 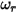 la velocidad de traslación y rotación (solo magnitud), este modelo de rebote se expresa de la siguiente manera:
la velocidad de traslación y rotación (solo magnitud), este modelo de rebote se expresa de la siguiente manera:◦ Traslación
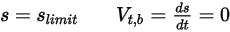
Ecuación 2.449
◦ Rotación
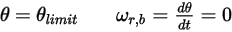
Ecuación 2.450
• Rebote parcial: modelo que dicta que cuando un cuerpo sólido o un límite alcanza el límite de su movimiento, cambia de dirección con la pérdida parcial de su energía cinética, determinada por un factor especificado por el usuario 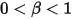 :
:
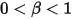 :
:◦ Traslación
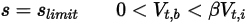
Ecuación 2.451
◦ Rotación
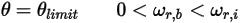
Ecuación 2.452
• Rebote perfecto: modelo que determina que cuando un cuerpo sólido o un límite alcanza el límite de su movimiento, cambia de dirección con pérdida cero de su energía cinética 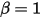 :
:
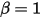 :
:◦ Traslación

Ecuación 2.453
◦ Rotación

Ecuación 2.454