Consideraciones numéricas
En modelos multifase homogéneos, sin tener en cuenta los deslizamientos de velocidad, no se requiere ningún tratamiento especial para resolver las ecuaciones de momento de la mezcla y la formulación del flujo volumétrico de cara. Esto se debe a que son las mismas que las ecuaciones que gobiernan los flujos de una sola fase de densidad variable. En este tema se pone el foco en la construcción de la ecuación de corrección de la presión y el tratamiento de las ecuaciones de fracción volumétrica de fase, especialmente, los esquemas de resolución de interfaz del modelo de VOF.
Ecuación de continuidad de volumen
Para satisfacer la restricción de continuidad y garantizar la estabilidad numérica, la ecuación de corrección de la presión se construye en función de la continuidad total del volumen, en lugar de la continuidad de la masa. Cuando la ecuación 2.57 de la fracción de continuidad/volumen de la fase qth se divide por una densidad de referencia de fase, ρrq, y se combinan todas las fases, se obtiene una ecuación de la continuidad total del volumen que satisface la ley de conservación de la masa:
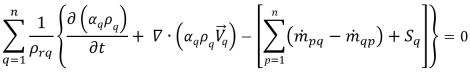
ecuación 2.135
donde la densidad de referencia de fase se suele definir como la densidad de fase, ρrq = ρq
La introducción de Ω como volumen de una celda de cálculo y la integración de la ecuación 2.135 sobre el volumen de control generan las ecuaciones algebraicas discretas:
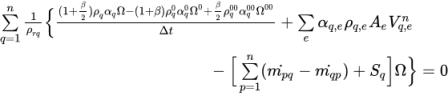
ecuación 2.136
Si se utiliza el mismo método que en el solver basado en la presión de una sola fase descrito en valores numéricos y se supone lo siguiente:
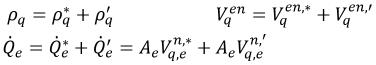
ecuación 2.137
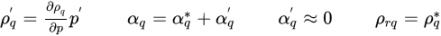
ecuación 2.138
se puede reorganizar la ecuación 2.136 como la siguiente ecuación de corrección:
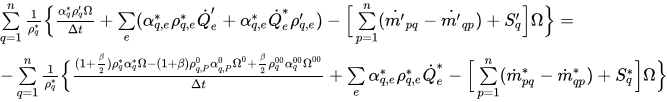
ecuación 2.139
Aquí * y ' representan los valores anteriores y las correcciones.
Δt | paso de tiempo |
Ae | área en la cara e |
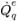 | flujo de volumen |
Siguiendo el mismo método que en el solver basado en la presión de una sola fase, aplique el tipo simple de algoritmos (Simple, SimpleC y SimpleS) para conectar las correcciones de velocidad y presión y obtener la ecuación de corrección de la presión para flujos multifase:
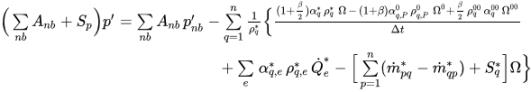
ecuación 2.140
donde,
Anb | coeficiente de vínculo |
Sp | término linealizado |
Ecuaciones de fracción volumétrica de fase
El transporte de una fracción volumétrica de fase está gobernado por la conservación de la masa de fase. Puesto que la conservación del volumen total se aplica a la formación de la ecuación de corrección de la presión, las ecuaciones reales resueltas para fracciones volumétricas de fase también aplican la conservación del volumen por coherencia numérica:
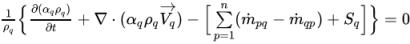
ecuación 2.141
Normalmente, para un sistema de n fases, solo se resuelven (n-1) ecuaciones, mientras que la fase nth se obtiene de la restricción física:
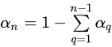
ecuación 2.142
Después del método de discretización, la formulación integral de la ecuación 2.141 es la siguiente:
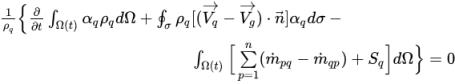
ecuación 2.143
Igual que en las ecuaciones de conservación del momento, la energía y el volumen total, los esquemas temporales de discretización son cruciales para la precisión numérica. Para las ecuaciones de fracción volumétrica, además de los esquemas de tiempo implícitos estándar, es una práctica habitual utilizar el avance de tiempo explícito con esquemas de advección del alta resolución para poder capturar las interfaces de los modelos de VOF con mayor precisión. En esta sección, se describen con detalle las formulaciones implícitas y explícitas de VOF.
• Formulación implícita de VOF
Con la formulación implícita de VOF, la ecuación de fracción volumétrica de fase discretizada tiene la siguiente expresión general:
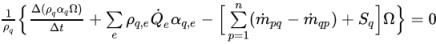
ecuación 2.144
En esta ecuación, la fracción volumétrica de fase αq en el paso de tiempo actual es una función de otras cantidades en el paso de tiempo actual. Por lo tanto, como las ecuaciones de corrección de la presión, energía y momento, la ecuación 2.144 de fracción volumétrica discretizada se resuelve iterativamente en cada paso de tiempo. En Creo Flow Analysis, la formulación implícita adoptada se resume de la siguiente manera:
◦ Esquemas de advección: el flujo volumétrico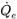 
se calcula en función del campo de flujo del paso de tiempo actual. El valor de cara αq,e es aproximado por lo que respecta a los valores de centro de la celda αq,P,αq,E y los gradientes (
,
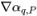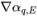) de las celdas vecinas P y E. Igual que en la ecuación escalar pasiva, los esquemas de advección tienen el formato general:
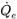se calcula en función del campo de flujo del paso de tiempo actual. El valor de cara αq,e es aproximado por lo que respecta a los valores de centro de la celda αq,P,αq,E y los gradientes (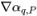,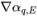) de las celdas vecinas P y E. Igual que en la ecuación escalar pasiva, los esquemas de advección tienen el formato general: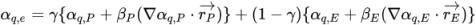
ecuación 2.145
Mediante la utilización de diferentes valores para los parámetros γ, βP y βE, así como los esquemas para calcular los gradientes de fracción volumétrica, se desarrollan cuatro esquemas de advección para las ecuaciones de fracción de volumen: contraviento de primer orden, contraviento de segundo orden, diferencia de centro y alta resolución.
◦ Esquemas temporales: para describir el esquema temporal implícito, se puede generalizar la ecuación 2.144 en la expresión que se indica a continuación.
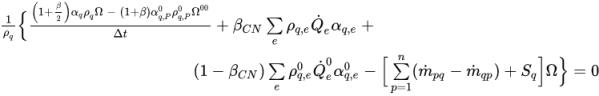
ecuación 2.146
Las variables sin superíndice son los valores del paso de tiempo actual. Las variables con el superíndice 0 o 00 indican los valores de los pasos de tiempo anteriores.
Los parámetros β y βCN varían entre 0 y 1, y determinan los esquemas de tiempo. En concreto, se adoptan tres esquemas temporales para la discretización de las ecuaciones de fracción volumétrica de fase:
▪ Contraviento de primer orden de Euler: β = 0, βCN = 1
▪ Segundo orden de tres niveles: β = 0, βCN = 1
▪ Método de Crank-Nicolson: β = 0, βCN = 0.6 (por defecto)
• Formulación explícita de VOF
Cuando se utiliza la formulación explícita para resolver las ecuaciones de VOF, las fracciones volumétricas de fase del paso de tiempo actual se calculan directamente en función de las cantidades conocidas del paso de tiempo anterior. Por lo tanto, la formulación explícita de VOF no requiere una solución iterativa para la ecuación 2.144 durante cada paso de tiempo. Sin embargo, dado que el resto de las ecuaciones de transporte se resuelven implícitamente, el paso de tiempo que se utiliza para el cálculo de la fracción volumétrica es generalmente menor que el paso de tiempo de las otras ecuaciones de transporte. Se debe determinar un paso de subtiempo para la formulación explícita de VOF, que se calcula automáticamente o que se puede proporcionar en Creo Flow Analysis.
Con la formulación explícita, la ecuación de fracción volumétrica de fase discretizada se formula como:
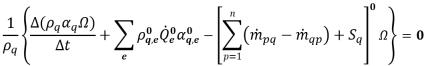
ecuación 2.147
donde los términos de advección y origen se calculan en función de las cantidades conocidas del paso de tiempo anterior. El flujo volumétrico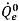 
se calcula de la misma manera que 
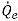en la formulación implícita. La fracción volumétrica de cara 
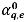también se puede estimar mediante uno de los cuatro esquemas de advección: contraviento de primer orden, contraviento de segundo orden, diferencia de centro y alta resolución.
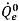se calcula de la misma manera que 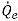en la formulación implícita. La fracción volumétrica de cara 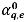también se puede estimar mediante uno de los cuatro esquemas de advección: contraviento de primer orden, contraviento de segundo orden, diferencia de centro y alta resolución.Creo Flow Analysis proporciona los tres algoritmos siguientes para los esquemas de avance de tiempo explícitos:
• Primer orden de Euler explícito: la ecuación de fracción volumétrica se discretiza de la manera que se indica a continuación.
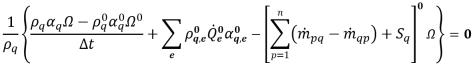
ecuación 2.148
• Segundo orden de Runge-Kutta: permite introducir la función que se indica a continuación.
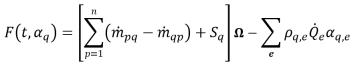
ecuación 2.149
La ecuación 2.147 se reescribe de la siguiente manera:
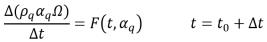
ecuación 2.150
El esquema explícito de Runge-Kutta de segundo orden tiene este formato:
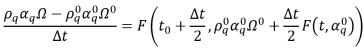
ecuación 2.151
• Cuarto orden de Runge-Kutta: para la ecuación de fracción volumétrica de la fase q, el esquema explícito de Runge-Kutta de cuarto orden tiene el formato que se indica a continuación.
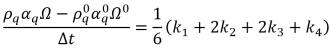
ecuación 2.152
donde:
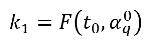
ecuación 2.153
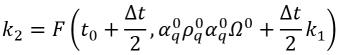
ecuación 2.154
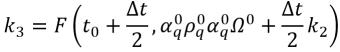
ecuación 2.155
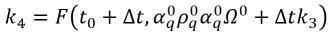
ecuación 2.156
Para el sistema de n fases, normalmente solo se resuelven (n-1) fracciones de volumen de fase y la restante se obtiene de la restricción física, ecuación 2.142. Sin embargo, también se pueden resolver las n ecuaciones de fracción volumétrica de fase y la ecuación 2.142 se satisface aplicando una escala a cada fase empleando la suma de la fracción volumétrica total calculada. Esto podría ser menor o mayor que 1 en un proceso iteractivo.