Modelos de flujo
El módulo Flow (Flujo) resuelve la conservación de masa y momento con las ecuaciones transitorias de Navier-Stokes H.Ding, F.C. Visser, Y.Jiang, and M. Furmanczyk, "Demonstration and Validation of a 3-D CFD Simulation Tool Predicting Pump Performance and Cavitation for Industrial Applications", FEDSM2009-78256, 2009.
La formulación integral (conservadora) de las ecuaciones promedio de Navier-Stokes de Reynold (RANS) es la siguiente:
• Continuidad
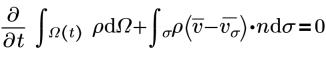
• Momento
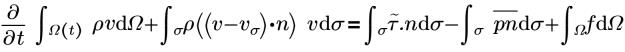
• Tensor de tensión
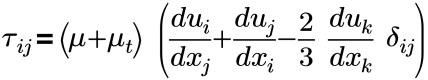
donde,
τij | tensión efectiva de corte (molecular+turbulenta) |
f | fuerza sobre el cuerpo |
n | normal de superficie |
ρ | presión estática (Pa) |
t | tiempo |
v | velocidad de fluido |
vσ | velocidad de malla |
Ω(t) | volumen de control como función de tiempo |
r | densidad de fluido local promedio (kg/m3) |
σ | superficie de volumen de control |
µ | viscosidad dinámica (poise o Pa-s) |
µt | viscosidad dinámica turbulenta |
δij | Delta de Kronecker(=1 para i=j, =0 para i≠j) |
Modelos de viscosidad
• Viscosidad dinámica constante (Constant Dynamic Viscosity): permite especificar la viscosidad del fluido en un volumen seleccionado. La unidad de viscosidad dinámica es Pa-s o N-s/m2.
El valor de la viscosidad dinámica se especifica en el cuadro en la selección de Viscosidad dinámica constante (Constant Dynamic Viscosity).
• Viscosidad cinemática constante (Constant Kinematic Viscosity): permite especificar la viscosidad del fluido en un volumen seleccionado. La unidad de viscosidad cinemática es m2/s. El valor de la viscosidad cinemática se especifica en el cuadro en la selección de Constant Kinematic Viscosity.
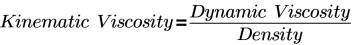
• Sutherland Law: permite especificar la viscosidad del fluido en un volumen seleccionado en términos de viscosidad dinámica (Pa-s). La ecuación y las entradas son las siguientes:
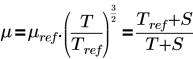
donde,
T | temperatura (K) |
µref | viscosidad en la temperatura de referencia (Pa-s) |
S | Temperatura de Sutherland (K) |
T es la temperatura (K) del fluido necesaria como entrada si el módulo de energía no está activo. |
La ley de Sutherland se utiliza para calcular la viscosidad de un gas ideal como función de temperatura. Sutherland, W. (1893), "The viscosity of gases and molecular force", Philosophical Magazine, S. 5, 36, pág. 507-531 (1893). En la siguiente tabla se muestra la constante y la temperatura de referencia de Sutherland para los gases seleccionados. Ref.: en.wikipedia.org/wiki/viscosity.
Gas | S (K) | Tref (K) | mref (Pa-s) |
|---|---|---|---|
aire | 120 | 291.15 | 18.27 e-6 |
nitrógeno | 111 | 300.55 | 17.81 e-6 |
oxígeno | 127 | 292.25 | 20.81 e-6 |
dióxido de carbono | 240 | 293.15 | 14.8 e-6 |
monóxido de carbono | 118 | 288.15 | 17.2 e-6 |
hidrógeno | 72 | 293.85 | 8.76 e-6 |
amoníaco | 370 | 293.15 | 9.82 e-6 |
dióxido sulfúrico | 416 | 293.65 | 12.54 e-6 |
helio | 79.4 | 273 | 19 e-6 |
Modelos no newtonianos de viscosidad
Los modelos no newtonianos de viscosidad son los siguientes:
• Modelo de Herschel-Bulkley
• Modelos de Bingham
Estos modelos proporcionan la viscosidad adecuada para los distintos tipos de fluidos que exhiben propiedades de flujo no newtonianas. El modelo de Herschel-Bulkley y los modelos de Bingham relacionan la tensión de corte con la velocidad de corte de la siguiente manera:
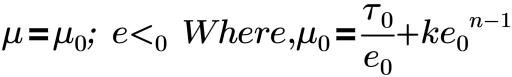
donde,
e0 | velocidad crítica de corte |
k | índice de coherencia |
τ0 | tensión de esfuerzo del fluido |
n | Índice de la ley potencial. Para el modelo de Bingham, n=1 |
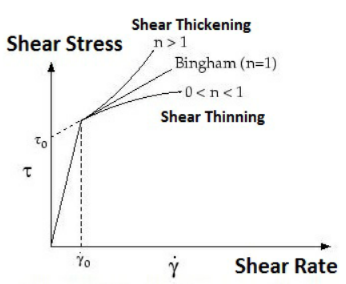
La velocidad de corte de 0 es la misma que el punto gamma del trazado anterior. |
Modelo de resistencia
Modelo de resistencia (Resistance Model) es una opción del módulo Flujo (Flow) que se puede utilizar para definir una resistencia en un volumen seleccionado. En la opción Modelo de resistencia (Resistance Model) se incluyen los dos modelos siguientes:
• Pérdida de presión (Pressure Loss): basado en ecuación que se indica a continuación.
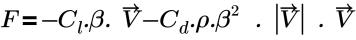
donde,
Cl | coeficiente de resistencia lineal (Pa-s/m2) |
Cd | coeficiente de resistencia cuadrática (1/m) |
β | porosidad |
ρ | Densidad |
• Ley de Darcy (Darcy's Law): modelo basado en la ecuación que se indica a continuación.
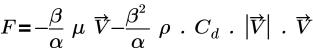
donde,
β | porosidad |
α | permeabilidad |
µ | viscosidad dinámica |
V | Velocidad |
Cd | coeficiente de resistencia cuadrática (1/m) |
La velocidad que se utiliza en la ecuación de resistencia es la velocidad local. F en la ecuación se mide en la unidad N/m3, como fuerza/volumen, gradiente de presión (Dp/Dx) o rg. La caída de presión a través de la interfaz se calcula mediante la multiplicación de F por un espesor finito. La porosidad se define en el módulo Común (Common).