Eulersche Modelle und zugrunde liegende Gleichungen
in diesem Abschnitt werden die zugrunde liegenden Gleichungen für die VOF (Volume of Fluid)- und Mischungs-Mehrphasenmodelle erläutert, die Turbulenz und Berandungen in Mehrphasenflüssen modellieren.
Allgemeine zugrunde liegende Gleichungen für Multiphase
Im Euler-Euler-Ansatz wird angenommen, dass die verschiedenen Phasen oder Komponenten eines Mehrphasensystems mathematisch einander durchdringende Kontinua sind. Da der physikalische Raum oder das Volumen von allen Phasen gemeinsam genutzt wird, wird das Konzept des Phasen-Volumen-Anteils eingeführt, um den Phasentransport zu beschreiben. Für die Phasen-Volumen-Anteile wird angenommen, dass sie kontinuierliche Funktionen von Raum und Zeit sind und ihre Summe gleich 1 ist. Erhaltungssätze werden für jede Phase angewendet, um einen Satz von zugrunde liegenden Gleichungen abzuleiten, die durch theoretische oder empirische konstitutive Beziehungen geschlossen werden. Im Euler-Euler-Ansatz für die Mehrphasen-Modellierung werden zwei Typen von Modellen regelmäßig verwendet:
• Inhomogenes oder Eulersches Multi-Fluid-Modell – Löst direkt die zugrunde liegenden Gleichungen jeder Phase, einschließlich der Phase des Impulses, der Energie, der Turbulenz, der Spezies und die Volumenanteilgleichungen. Die Interaktionen von Phase zu Phase, die Interphasen-Übergänge von Impuls, Masse, Spezies und Wärme werden durch physikalische Untermodelle modelliert.
Unter Verwendung des allgemeinen Phasenskalars ϕq, q für die q-te Phase hat die verallgemeinerte Gleichung für die Phase q die folgende Form:
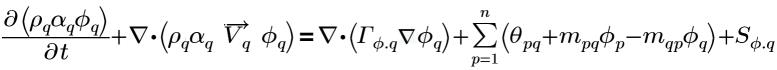
Gleichung 2.54
Dabei gilt:
ρq | Dichte q |
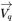 | Geschwindigkeit |
Sϕq | Quellenterm |
Tϕq | Diffusionskoeffizient |
αq | Volumenanteil der q-ten Phase |
und ϕq stellt die abhängigen Variablen in einem Mehrphasensystem dar:
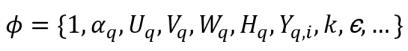
Gleichung 2.55
Dabei gilt:
Uq, Vq, Wq | Phasengeschwindigkeitskomponenten |
Hq | Gesamtenthalpie der Phase |
Yqi | Massenanteil der Spezies "i" in der q-ten Phase |
k | Kinetische Turbulenzenergie |
ε | kinetische Turbulenzenergie-Dissipationsrate für k-ε-Modelle |
In Gleichung 2.54 stellt der zweite Term rechts den Interphasen-Austausch dar. Speziell gilt:
p | p-te Phase |
n | Anzahl der Phasen im Mehrphasensystem |
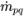 | Massenübergang von der q-ten Phase zur p-ten Phase |
θpq | direkter Phasenaustausch der transportierenden Mengen einschließlich Impuls, Energie und Spezies |
Durch die Verwendung von Untermodellen für den Interphasen-Austausch von Spezies, Masse, Impuls und Wärme können Sie den vollständigen Satz von zugrunde liegenden Gleichungen aus den Transportgleichungen ableiten, die hier verallgemeinert werden.
• Homogenes Mehrphasenmodell – Vereinfachte und ökonomische Alternative zum inhomogenen Modell. Der homogene Modellierungsansatz mittelt die den Phasen zugrunde liegenden Gleichungen von Fluss, Energie und Turbulenz, um einen Satz von Mischungstransportgleichungen zu erhalten, während die Phasen-Volumen-Anteile weiterhin gelöst werden. Für den Mischungsskalar ϕm hat die verallgemeinerte zugrunde liegende Gleichung den folgenden Ausdruck:
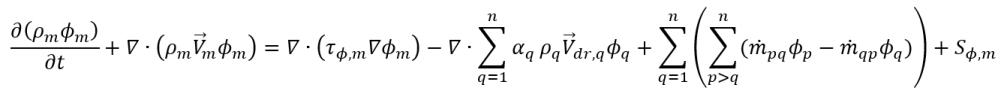
Gleichung 2.56
Dabei gilt:
m | Mischung von Phasen |
alle Variablen mit m | mischungs- oder phasengemittelte Werte |
und 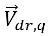 ist die Differenz zwischen der Geschwindigkeit der Phase q und der Mischungsgeschwindigkeit:
ist die Differenz zwischen der Geschwindigkeit der Phase q und der Mischungsgeschwindigkeit:
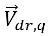 ist die Differenz zwischen der Geschwindigkeit der Phase q und der Mischungsgeschwindigkeit:
ist die Differenz zwischen der Geschwindigkeit der Phase q und der Mischungsgeschwindigkeit: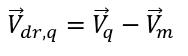
Das homogene Mehrphasenmodell ist ein Grenzfall des Euler-Euler-Mehrphasenflusses, in dem die Interphasen-Übertragungsrate groß ist. Die grundlegende Annahme ist, dass alle Phasen das gleiche Druckfeld gemeinsam nutzen. Mit dieser Annahme hat das homogene Modell eine weitere Vereinfachung des vollständig inhomogenen Eulerschen Multi-Fluid-Modell zum Ergebnis, indem angenommen wird, dass alle Phasen ein gemeinsames Geschwindigkeits-, Temperatur- und Turbulenzfeld gemeinsam nutzen. Dieser Ansatz ist ein guter Ersatz für das vollständige Eulersche Multi-Fluid-Modell, da er einfach zu implementieren und wirtschaftlich zu berechnen ist. Physikalisch kann das homogene Modell, ohne die Anforderung von Interphasen-Austauschmodellen in Impuls- und Energiegleichungen, in Fällen wie freien Oberflächenflüssen (VOF), Kavitation und anderen hochgradig gemischten Mehrphasenflüssen eine ebenso gute Leistung wie das vollständige Multi-Fluid-Modell bringen.
In Creo Flow Analysis übernimmt das aktuelle Modul "Multiphase" nur den homogenen Modellierungsansatz. Der Fokus liegt auf der Modellierung des freien Oberflächenflusses (Volume of Fluid-Modell) und der homogenen Flüssigkeit-Gas-Zweiphasenflüsse (Mischungsmodell). Im Prinzip können Sie die Modellierungsfunktion für n Phasenflüsse anwenden.
VOF- und Mischungs-Mehrphasenmodelle
Die Volume of Fluid (VOF)- und Mischungs-Mehrphasenmodelle verwenden den homogenen Modellierungsansatz. Die Transportgleichung des Volumenanteils in jeder Phase wird aus Gleichung 2.54 bezogen. Die zugrunde liegenden Gleichungen für den Mischungsimpuls und die Mischungsenergie werden unter Verwendung der Gleichung 2.56 und den Erhaltungssätzen von Masse, Impuls und Energie abgeleitet. Der Satz der zugrunde liegenden Gleichungen wird in diesem Abschnitt dargestellt.
• Phase-q-Volumenanteil-Gleichung
In Gleichung 2.54, Einstellung ϕq=1, wird die Phase-q-Volumenanteil-Gleichung bezogen:
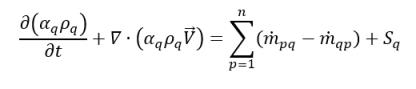
Gleichung 2.57
Hierbei stellt die Rate der Massenaustauschterme 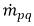 und
und 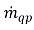 den Betrag von Quelle bzw. Senke für die Phase q dar. In einem Interphasen-Massenübergangsprozess ist einer der beiden Terme normalerweise null. Siehe hierzu das folgende Beispiel:
den Betrag von Quelle bzw. Senke für die Phase q dar. In einem Interphasen-Massenübergangsprozess ist einer der beiden Terme normalerweise null. Siehe hierzu das folgende Beispiel:
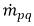 und
und 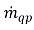 den Betrag von Quelle bzw. Senke für die Phase q dar. In einem Interphasen-Massenübergangsprozess ist einer der beiden Terme normalerweise null. Siehe hierzu das folgende Beispiel:
den Betrag von Quelle bzw. Senke für die Phase q dar. In einem Interphasen-Massenübergangsprozess ist einer der beiden Terme normalerweise null. Siehe hierzu das folgende Beispiel:In einem Verdampfungsprozess verliert die Flüssigphase q Masse, 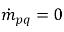 und
und 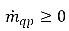 , während in der Dampfphase
, während in der Dampfphase 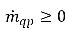 und
und 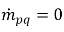 ist.
ist.
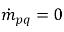 und
und 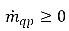 , während in der Dampfphase
, während in der Dampfphase 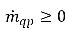 und
und 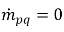 ist.
ist.Beim n-Phasensystem erfüllt die Summe der Phasen-Volumen-Anteile die physikalische Randbedingung:
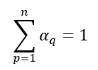
Gleichung 2.58
Oder die Gesamtmassenerhaltung:
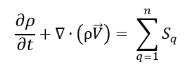
Gleichung 2.59
wobei die Mischungsmengen wie folgt definiert sind:
◦ Volumengemittelte Mischungsdichte
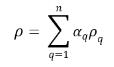
Gleichung 2.60
◦ Massegemittelte Mischungsgeschwindigkeit
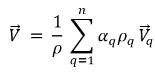
Gleichung 2.61
• Mischungsimpulsgleichung – Ermittelt durch Summieren der einzelnen Impulsgleichungen für alle Phasen im System. Aus Gleichung 2.56 erhalten Sie durch Festlegen von 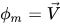
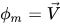
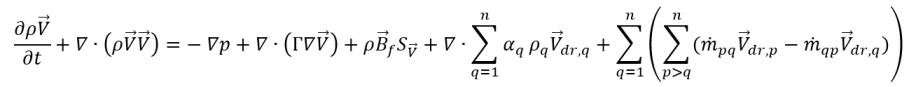
Gleichung 2.62
Hierbei sind die Mischungsmengen im Folgenden definiert:
◦ Volumengemittelte Mischungsviskosität:

Gleichung 2.63
Der Diffusionskoeffizient Γ in Gleichung 2.62 wird unter Verwendung der dynamischen Viskosität µ und der turbulenten Viskosität μt der Mischung berechnet. Die letzten zwei Terme rechts stellen die direkte Impulsübertragung und den durch den Massenübergang eingeleiteten Impulsaustausch dar. Sie werden durch die Phasendriftgeschwindigkeiten bestimmt, 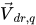 , definiert als:
, definiert als:
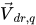 , definiert als:
, definiert als:
Gleichung 2.69
Im homogenen Ansatz können Sie diese Driftgeschwindigkeit mithilfe eines algebraischen Modells modellieren. Im aktuellen VOF- und Mischungs-Modell wir jedoch kein Schlupf zwischen den Phasen angenommen:
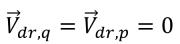
Daher sind beide Impulsaustauschterme null.
◦ Mischungsenergiegleichung
Ohne den Geschwindigkeitsschlupf nimmt die Energiegleichung für die Mischung die folgende Form an:
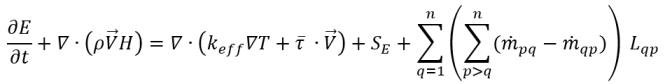
Gleichung 2.70
Hierbei sind die Mischungsvariablen wie folgt definiert:
▪ Volumengemittelte Wärmeleitfähigkeit
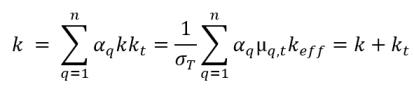
Gleichung 2.71
▪ Massegemittelte Mischungsenergie und -enthalpie
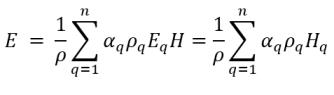
Gleichung 2.72
In der Mischungsenergiegleichung Gleichung 2.70 wird der viskose Wärmeterm 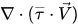 wie in einem Einphasenfluss berechnet; und SE ist die gesamte externe oder Benutzerwärmequelle.
wie in einem Einphasenfluss berechnet; und SE ist die gesamte externe oder Benutzerwärmequelle.
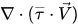 wie in einem Einphasenfluss berechnet; und SE ist die gesamte externe oder Benutzerwärmequelle.
wie in einem Einphasenfluss berechnet; und SE ist die gesamte externe oder Benutzerwärmequelle.Der letzte Term rechts ist die Schnittstellen-Wärmeübertragung, verursacht durch den Massenübergang. Unter der Annahme, dass die Phasen die gleiche Temperatur teilen, ist Lgp abhängig von der Definition von Hq und Hp in der gelösten Energiegleichung.
Wie im Modul Wärme (Heat) beschrieben, besteht die statische Enthalpie eines Materials aus zwei Teilen: Normzustand-Referenzenthalpie und fühlbare Enthalpie. Unter der Annahme, dass Phase-q flüssig ist und Phase-p Dampf ist, haben wir die folgenden statischen Gesamtenthalpien für die Phasen:
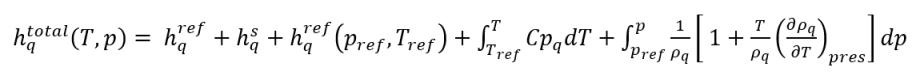
Gleichung 2.73
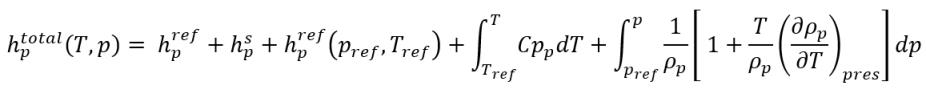
Gleichung 2.74
Dabei gilt:
pref | Referenzdruck |
Tref | Referenztemperatur |
hq,ref | Normzustand-Referenzenthalpien für Phase-q |
hp,ref | Normzustand-Referenzenthalpien für Phase-p |
Die Differenz der Referenzenthalpien
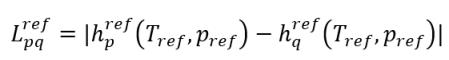
Gleichung 2.75
ist die latente Wärme bei der Referenztemperatur Tref und dem Referenzdruck pref.
▪ Einschließlich der Standardreferenzenthalpie:
Wenn in Gleichung 2.70 die Enthalpie H die Gesamtmischungsenthalpie ist, ergibt sich
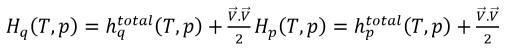
Gleichung 2.76
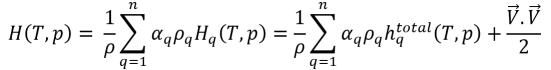
Gleichung 2.77
Dann ist die Differenz aufgrund der Phasenbildungsenthalpien oder der latenten Wärme Lpq bereits in die Energiegleichung eingeschlossen. Die Menge wird auf null gesetzt:
Lpq=0
Die Wärmeübertragung aufgrund des Massenübergangs, der letzte Term rechts in Gleichung 2.70, ist in der Mischungsenergiegleichung gleich null.
▪ Ohne die Standardreferenzenthalpie:
In einem CFD-Gleichungslöser wird die Gesamtenthalpie nicht direkt gelöst. Stattdessen wird nur die fühlbare Enthalpie relativ zur Sättigungstemperatur in die gelöste Enthalpie und die innere Energie eingeschlossen:
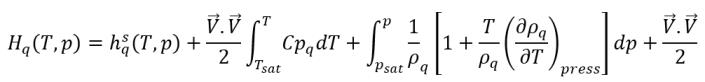
Gleichung 2.79
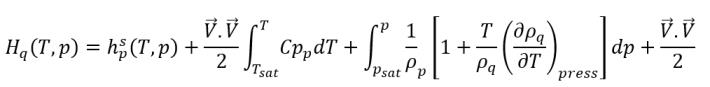
Gleichung 2.80
In diesem Fall ist Lpq nicht null. Er sollte die latente Wärme sein:
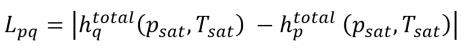
Gleichung 2.81
Dabei gilt:
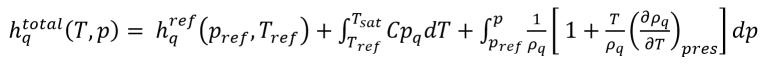
Gleichung 2.82
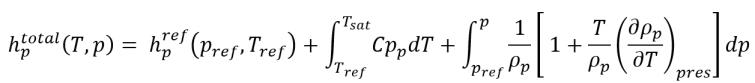
Gleichung 2.83
In Creo Flow Analysis wird standardmäßig wird die Normzustand-Referenzenthalpie automatisch berücksichtigt. Eine Benutzereingabe ist nicht erforderlich.
Turbulenzmodelle
• Mischungs-k-ε Turbulenzmodelle
In den Volume of Fluid (VOF)- und Mischungsmehrphasen-Modellen wird der Turbulenzeffekt auf die Phasenmischung berücksichtigt, indem die Erweiterungen der Einphasen-Turbulenzmodelle verwendet werden. Die Turbulenzmodelle und die wandnahen Behandlungen, die im Modell Turbulence beschrieben sind, werden in Creo Flow Analysis auf die Multiphasenflüsse ausgedehnt. Mit den Mischungsflussmengen haben die Standard- und RNG-k-ε Modelle die gleichen allgemeinen Formen wie in den Einphasen-Turbulenzmodellen:
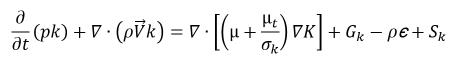
Gleichung 2.84
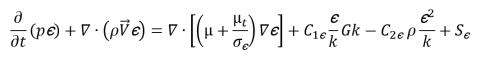
Gleichung 2.85
Hierbei werden die Mischungsdichte ρ, die Geschwindigkeit 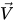 und die molekulare Viskosität μ aus den jeweiligen Phasenwerten unter Verwendung der Beziehungen in Gleichung 2.60, Gleichung 2.61 und Gleichung 2.63 berechnet; Sk und Sε umfasst sowohl mögliche externe und Benutzerquellen als auch die Phaseninteraktionsquellen. Die turbulente Viskosität für die Mischung μt wird direkt aus dem Ausdruck berechnet:
und die molekulare Viskosität μ aus den jeweiligen Phasenwerten unter Verwendung der Beziehungen in Gleichung 2.60, Gleichung 2.61 und Gleichung 2.63 berechnet; Sk und Sε umfasst sowohl mögliche externe und Benutzerquellen als auch die Phaseninteraktionsquellen. Die turbulente Viskosität für die Mischung μt wird direkt aus dem Ausdruck berechnet:
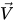 und die molekulare Viskosität μ aus den jeweiligen Phasenwerten unter Verwendung der Beziehungen in Gleichung 2.60, Gleichung 2.61 und Gleichung 2.63 berechnet; Sk und Sε umfasst sowohl mögliche externe und Benutzerquellen als auch die Phaseninteraktionsquellen. Die turbulente Viskosität für die Mischung μt wird direkt aus dem Ausdruck berechnet:
und die molekulare Viskosität μ aus den jeweiligen Phasenwerten unter Verwendung der Beziehungen in Gleichung 2.60, Gleichung 2.61 und Gleichung 2.63 berechnet; Sk und Sε umfasst sowohl mögliche externe und Benutzerquellen als auch die Phaseninteraktionsquellen. Die turbulente Viskosität für die Mischung μt wird direkt aus dem Ausdruck berechnet: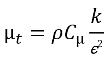
Gleichung 2.86
während die Produktion der kinetischen Turbulenzenergie auf der Basis der turbulenten Viskositäts- und Geschwindigkeitsgradienten der Mischung berechnet wird:
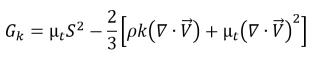
Gleichung 2.87
Hierbei ist S der Modul der mittleren Dehnungsrate der Mischung, 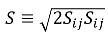
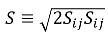
Die turbulente Viskosität für Phase-q kann berechnet werden als:
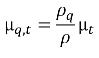
Gleichung 2.87
• Effekt der turbulenten Diffusion
Bei mehrphasigen turbulenten Flüssen entsteht eine turbulente Dispersionskraft, wenn der momentane Grenzflächenwiderstandsterm gemittelt wird, die wie die bei der Phasendiffusion agiert. Das inhomogene Eulersche Multi-Fluid-Modell behandelt diesen Turbulenzeffekt im Allgemeinen als zusätzliche Interphasen-Kraft, die durch die Gradienten der Phasen-Volumen-Anteile in Phasenimpulsgleichungen bestimmt wird. Dieser Turbulenzeffekt kann auch modelliert werden, indem er direkt als Term der turbulenten Diffusion in den Phasenvolumenanteilsgleichungen betrachtet wird. Durch Dividieren von 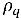 und Gruppieren aller Quellen als
und Gruppieren aller Quellen als 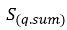 (die Summe von Interphasen-Massenübergangs und externen Massenquellen) gelangt man zu der folgenden zugrunde liegenden Gleichung für den Phase-q-Volumenanteil in turbulenten Flüssen:
(die Summe von Interphasen-Massenübergangs und externen Massenquellen) gelangt man zu der folgenden zugrunde liegenden Gleichung für den Phase-q-Volumenanteil in turbulenten Flüssen:
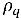 und Gruppieren aller Quellen als
und Gruppieren aller Quellen als 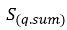 (die Summe von Interphasen-Massenübergangs und externen Massenquellen) gelangt man zu der folgenden zugrunde liegenden Gleichung für den Phase-q-Volumenanteil in turbulenten Flüssen:
(die Summe von Interphasen-Massenübergangs und externen Massenquellen) gelangt man zu der folgenden zugrunde liegenden Gleichung für den Phase-q-Volumenanteil in turbulenten Flüssen: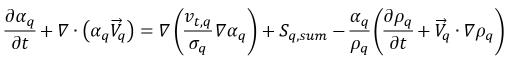
Hierbei ist der erste Term auf der rechten Seite der Term der turbulenten Diffusion in Phase-q ist, der die folgende Randbedingung erfüllen muss, damit die Gesamtmassenerhaltung erfüllt ist:
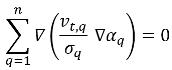
Die Terme der turbulenten Diffusion werden in der Regel als Option implementiert. Standardmäßig sind sie nicht eingeschlossen.
Modellierung von Mehrphasenberandungen
In Volume of Fluid (VOF)- und Mischungs-Mehrphasenmodellen sind die Randbedingungen für Fluss- und Energiegleichungen die gleichen wie für die einphasigen Flüsse. Diese werden in den Modulen Flow und "Heat" beschrieben. Für die Phasen-Volumen-Anteile werden nur feste Werte und Null-Gradienten im Folgenden angewendet:
• n-Phase-Einlass-Berandung
Für (n-1) Phasen sind die Einlassvolumenanteile vorbestimmt, während die n-te Phase unter Verwendung der physikalischen Randbedingung ermittelt wird:
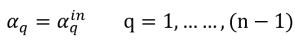
Gleichung 2.88
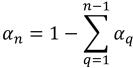
Gleichung 2.89
Der Volumenanteil jeder Phase darf nicht negativ sein.
• Auslass/Symmetrie/Wand-Berandung
Für (n-1) Phasen gelten die Null-Gradienten-Bedingungen für alle Auslass-, Symmetrie- und Wandberandungen, während die n-te Phase unter Verwendung der physikalischen Randbedingung ermittelt wird:
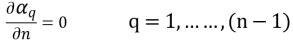
Gleichung 2.90
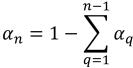
Gleichung 2.91
Die oben genannten zugrunde liegenden Gleichungen, Turbulenzmodelle und Randbedingungen bilden die Grundlage der homogenen VOF- und Mischungs-Mehrphasenmodelle. Ohne externe oder Benutzerquellenausdrücke und Interphasen-Massenübergänge sind sie ein geschlossenes Gleichungssystem und werden mit einem druckbasierten Finite-Volume-Mehrphasen-Gleichungslöser numerisch gelöst. Viele praktische Anwendungen erfordern spezifische Untermodelle wie die Oberflächenspannungskraft in VOF-Modellen und Interphasen-Massenübergänge, um die entsprechenden physikalischen Phänomene und Prozesse genau zu erfassen. Anstatt die Untermodelle in externe oder Benutzerquellen zusammenzufassen, wird empfohlen, sie direkt in die integrierten Modelle einzuschließen.