流體體積 (VOF) 模型的特殊考量
VOF 模型與混合模型
在均相尤拉 多相建模法中,流體體積 (VOF) 與混合尤拉模型皆會求解相同的一組混合物 (平均) 統御方程式。但是,它們以不同的物理機制為基礎,且適用於不同的多相流狀態:
• 混合模型 - 針對會被視為互穿連續體的二相或多相 (流體或微粒) 所設計。它會為混合物動量方程式與能量方程式求解,且不會追蹤相與相之間的界面,也不會觀察明顯界面。混合模型的應用包括處於低負載狀態下的含微粒流、氣泡與液滴流、沈積以及旋風分離器。您也可以使用已為分散相指定相對速度的混合模型來建模非均相多相流。
• VOF 模型 - 通常是一種瞬態表面追蹤法,針對相與相間界面位置受到關注的二或多種不混溶流體所設計。在 VOF 模型中,所有相會共用一組混合物動量與能量方程式,並會以隱式方式求解。您可使用平流法階數較高的精確顯式或隱式時間演算法,來取得相體積分數,以為一對相之間的明顯界面求解。VOF 模型的一般應用包括層變流、自由表面流、填充、攪動、大氣泡在液體中的運動、潰壩之後液體的運動、預測噴射斷裂 (表面張力) 以及追蹤任何液氣界面。
VOF 公式依賴於二或多種流體 (或相) 並不會相互穿透這項事實。因此在任何給定的控制體積單元中,局部相體積分數可以單獨確定其是僅包含其中一個相,還是混合相。例如,對於第 q 相,如果單元中的體積分數是 αq,則只有下列三個條件可行:
◦ αq = 0:單元缺乏第 q 相
◦ αq = 1:單元充滿第 q 相
◦ 0< αq < 1:單元包含第 q 相與一或多個其他相之間的界面。
因此,您可以透過求解一或多個相的體積分數的傳輸方程式,完成追蹤相之間的界面。
表面張力效應
表面張力是流體表面的彈性傾向,這可以使其取得可能的最小表面面積。請考慮液體中的空氣泡泡。在氣泡中,分子上的淨力會因它的鄰近分子而為零。在液氣界面中,表面張力源自液體分子彼此之間因凝聚所產生的更大引力 (相較於與空氣中分子間因附著所產生的引力而言)。淨效應是其表面的徑向內向力,它可以使氣泡收縮。氣泡內的壓力會增加,以抵銷分子間的吸引力。
• 連續體表面力模型
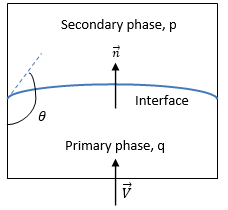
在 Creo Flow Analysis 中,VOF 模型可能包括表面張力效應以及每一對相之間的界面。所採用的表面張力模型以 Brackbill 等人提出的「連續體表面力」(Continuum Surface Force, CFS) 模型為基礎。此方法會將表面張力效應視為集中在界面的一種額外容量力,而非表面力。對於圖 2.26 所示的自由表面界面,主流體為相 q (液相),次流體為相 p (通常為氣相)。根據連續體表面力模型,表面曲率是使用表面法向在界面的局部梯度計算所得。將 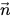 作為表面法向向量,定義為主流體體積分數的梯度,αq:
作為表面法向向量,定義為主流體體積分數的梯度,αq:
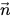 作為表面法向向量,定義為主流體體積分數的梯度,αq:
作為表面法向向量,定義為主流體體積分數的梯度,αq: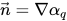
界面曲率 k 在單位法向向量散度的各項中定義:
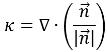
方程式 2.93
其中,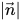 是向量
是向量 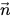 的量值。
的量值。
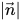 是向量
是向量 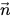 的量值。
的量值。表面的表面張力可以使用散度定理表示為容量力,其為新增到混合物動量方程式的額外一項源項。
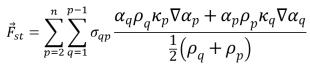
方程式 2.94
其中,σqp 是流體 q 與流體 p 之間的表面張力係數,單位為 N/m。方程式 2.94 允許在存在二個相以上的單元附近平滑疊加力。如果一個單元只有兩個相存在,您會擁有下列關係:
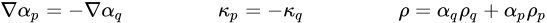
方程式 2.95
其中,ρ 是混合物密度。然後方程式 2.94 減少為
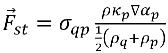
方程式 2.96
• 包括表面張力
表面張力效應的重要性由兩個無因次參數所決定:雷諾數 Re 與毛細數 Ca,或雷諾數與韋伯數 We:
如果 Re<<1,則關注的參數是毛細數:
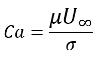
方程式 2.97
其中,U∞ 是自由流速度。如果 Ca>>1,由於表面張力過小,可忽略表面張力效應。
如果 Re>>1,則關注的參數是韋伯數:
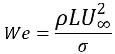
方程式 2.98
其中,L 是特徵長度。如果 We>>1,當慣性力比表面張力大很多時,也可以忽略表面張力效應。
壁附著 (接觸角)
流體體積 (VOF) 模型提供一個選項,用來指定與曲面張力模型搭配使用的壁附著力角度。根據 Brackbill 等人的理論,而非直接根據此邊界條件在壁的應用,流體與壁之間在界面的接觸角可用來調整壁附近單元中的表面法向。這個所謂的動態邊界條件會導致壁附近表面的曲率發生調整。
如果 θ 是自由表面界面在壁的接觸角 (如圖 2.26 所示),那麼近壁單元的單位法向向量計算方式如下:
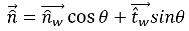
方程式 2.99
其中,
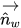 | 法向於壁的單位向量 |
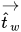 | 與壁相切的單位向量 |
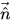 來確定表面的局部曲率,
來確定表面的局部曲率,