ODE 求解器
分別控制邊界和體積塊的 1-DOF 平移及旋轉常微分方程式 (ODE) 方程式 2.432 與方程式 2.444 以數值方式在 Creo Flow Analysis 中求解。具體而言,欲計算邊界與體積塊之用於重新網格化的移動與位移,請採用下列時間推進配置對 ODE 方程式進行積分:剛性、歐拉、Runge-Kutta 顯式求解器。
1-DOF 平移方程式的積分
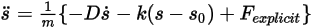
方程式 2.455
其中顯式計算的力項 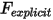 是:
是:
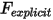 是:
是: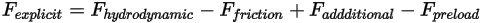
方程式 2.456
指定初始與邊界條件後,使用顯式時間推進配置對方程式 2.455 進行積分來獲得固體主體的位移。針對時間步長 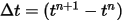 ,必須使用一般公式,如下所示:
,必須使用一般公式,如下所示:
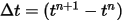 ,必須使用一般公式,如下所示:
,必須使用一般公式,如下所示: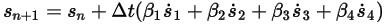
方程式 2.457
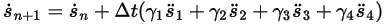
方程式 2.458
其中加權係數的總和為 1:
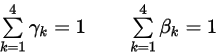
方程式 2.459
選擇加權係數可衍生不同的配置。例如,歐拉與 Runge-Kutta 顯式配置如下所示:
• 歐拉顯式求解器 (第 1 階)
透過 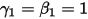 與
與 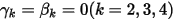 ,可使用如下歐拉顯式配置:
,可使用如下歐拉顯式配置:
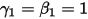 與
與 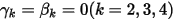 ,可使用如下歐拉顯式配置:
,可使用如下歐拉顯式配置: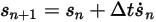
方程式 2.460
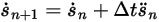
方程式 2.461
• Runge-Kutta 顯式求解器
Runge-Kutta 求解器是第 2 階與第 4 階顯式配置,如下所示:
◦ 第二階配置
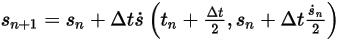
方程式 2.462
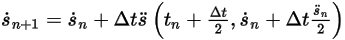
方程式 2.463
◦ 第四階配置
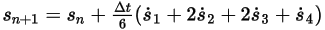
方程式 2.464
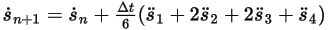
方程式 2.465
其中,

方程式 2.466

方程式 2.467

方程式 2.468

方程式 2.469
• 剛性求解器 (顯式)
除了標準歐拉與 Runge-Kutta 配置外,Creo Flow Analysis 已研發出其剛性求解器,以對平移 1-DOF ODE 方程式進行積分。此選項是固體主體動態運動的預設方法。
1-DOF 旋轉方程式的積分
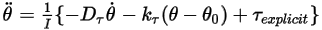
方程式 2.470
其中顯式計算的扭矩項 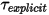 是:
是:
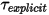 是:
是: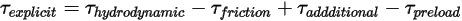
方程式 2.471
指定初始與邊界條件後,使用顯式時間推進配置對方程式 2.470 進行積分來獲得旋轉角度。針對時間步長 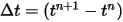 ,必須使用一般公式,如下所示:
,必須使用一般公式,如下所示:
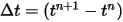 ,必須使用一般公式,如下所示:
,必須使用一般公式,如下所示: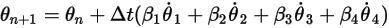
方程式 2.472
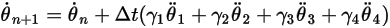
方程式 2.473
其中加權係數的總和為 1:
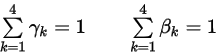
方程式 2.474
選擇加權係數可輕鬆衍生不同的數值配置。同樣地,歐拉與 Runge-Kutta 顯式配置如下:
• 歐拉顯式求解器 (第 1 階)
透過 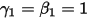 與
與 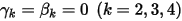 ,可使用如下歐拉顯式配置:
,可使用如下歐拉顯式配置:
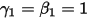 與
與 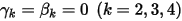 ,可使用如下歐拉顯式配置:
,可使用如下歐拉顯式配置: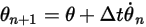
方程式 2.475
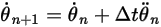
方程式 2.476
• Runge-Kutta 顯式求解器
Runge-Kutta 求解器是第 2 階與第 4 階顯式配置,如下所示:
◦ 第二階配置
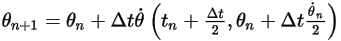
方程式 2.477
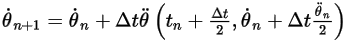
方程式 2.478
◦ 第四階配置
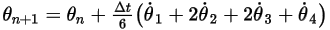
方程式 2.479
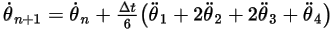
方程式 2.480
其中,

方程式 2.481

方程式 2.482

方程式 2.483

方程式 2.484
• 剛性求解器 (顯式)
除了標準歐拉與 Runge-Kutta 配置外,Creo Flow Analysis 已研發出其剛性求解器,以對 1-DOF 旋轉 ODE 方程式 2.444 進行積分。此選項是固體主體動態運動的預設方法。
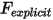 。為簡潔起見,您可採用下列格式重寫運動的 1-DOF 平移方程式:
。為簡潔起見,您可採用下列格式重寫運動的 1-DOF 平移方程式: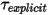 。為簡潔起見,您可採用下列格式重寫運動的 1-DOF 旋轉方程式 (
。為簡潔起見,您可採用下列格式重寫運動的 1-DOF 旋轉方程式 (