剛體運動
在模擬中,固體物件的曲面通常是流域中的壁邊界。當固體物件或曲面受到動態力和機械力以及熱效應的作用時,若受到的淨力不平衡,則可能會導致主體移動與變形。在流動模擬中,固體物件通常被視為剛體。因此,對於受力不平衡的固體物件,假設它可以線性方式移動 (平移) 和/或以一定的角度移動 (旋轉),而不發生任何變形。例如,對於 CFA 計算域,邊界移動會導致域發生變化,因此,體積塊網格可能會變形,如流動模組中所述。
對於剛體,可透過線動量與角動量守恆直接推導出控制其運動的方程式:
• 線動量 (平移)
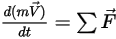
方程式 2.426
• 角動量 (旋轉)
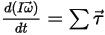
方程式 2.427
在方程式 2.426 中,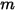 是移動物件的質量;
是移動物件的質量;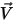 ⃗ 是線性/平移速度;而
⃗ 是線性/平移速度;而 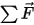 ⃗ 是施加於平移主體的總力/淨力。在方程式 2.427 中,
⃗ 是施加於平移主體的總力/淨力。在方程式 2.427 中,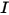 是慣性矩;
是慣性矩;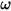 ⃗ 是角速度;而
⃗ 是角速度;而 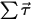 ⃗ 是作用於旋轉體的總扭矩/凈扭矩。
⃗ 是作用於旋轉體的總扭矩/凈扭矩。
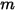 是移動物件的質量;
是移動物件的質量;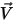 ⃗ 是線性/平移速度;而
⃗ 是線性/平移速度;而 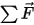 ⃗ 是施加於平移主體的總力/淨力。在方程式 2.427 中,
⃗ 是施加於平移主體的總力/淨力。在方程式 2.427 中,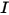 是慣性矩;
是慣性矩;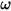 ⃗ 是角速度;而
⃗ 是角速度;而 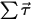 ⃗ 是作用於旋轉體的總扭矩/凈扭矩。
⃗ 是作用於旋轉體的總扭矩/凈扭矩。方程式 2.426 和方程式 2.427 用於控制固體主體的一般運動,這些運動具有六個自由度 (6-DOF),其中平移 (3-DOF) 和旋轉 (3-DOF) 分別具有三個自由度。Creo Flow Analysis 僅考量本節中所述的 1-DOF 平移與旋轉。
1-DOF 平移
假設固體主體沿著任意指定的方向 (保持不變) 作線性移動 (由單位向量 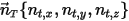 定義),則該主體的平移運動會減少為一個自由度 (1-DOF)。因此,根據線動量守恆,方程式 2.426 會沿著移動方向變成純量方程式,因為移動速度和力是由
定義),則該主體的平移運動會減少為一個自由度 (1-DOF)。因此,根據線動量守恆,方程式 2.426 會沿著移動方向變成純量方程式,因為移動速度和力是由 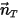 表示的:
表示的:
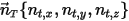 定義),則該主體的平移運動會減少為一個自由度 (1-DOF)。因此,根據線動量守恆,方程式 2.426 會沿著移動方向變成純量方程式,因為移動速度和力是由
定義),則該主體的平移運動會減少為一個自由度 (1-DOF)。因此,根據線動量守恆,方程式 2.426 會沿著移動方向變成純量方程式,因為移動速度和力是由 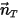 表示的:
表示的: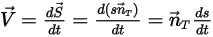
方程式 2.428
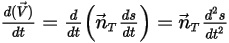
方程式 2.429
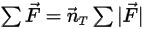
方程式 2.430
其中,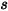 是沿移動方向
是沿移動方向 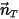 運動的固體主體上某一關注點處位置向量
運動的固體主體上某一關注點處位置向量 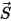 的量值。在笛卡兒座標系中,可以得到
的量值。在笛卡兒座標系中,可以得到
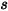 是沿移動方向
是沿移動方向 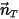 運動的固體主體上某一關注點處位置向量
運動的固體主體上某一關注點處位置向量 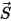 的量值。在笛卡兒座標系中,可以得到
的量值。在笛卡兒座標系中,可以得到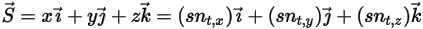
方程式 2.431
如果固體主體的質量保持恆定,並且展開的力項以顯性方式包含施加於主體的全部力,則所得純量線動量方程式的形式如下:
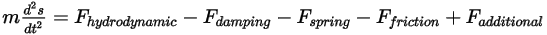
方程式 2.432
右邊的力指示下列內容:
• 流體動力  - 由壓力與剪切力構成。它們是由流體流與接觸流的固體主體曲面之間的相對運動引起的。壓力與剪切力是透過流解 (輸出量) 求得的:
- 由壓力與剪切力構成。它們是由流體流與接觸流的固體主體曲面之間的相對運動引起的。壓力與剪切力是透過流解 (輸出量) 求得的:
 - 由壓力與剪切力構成。它們是由流體流與接觸流的固體主體曲面之間的相對運動引起的。壓力與剪切力是透過流解 (輸出量) 求得的:
- 由壓力與剪切力構成。它們是由流體流與接觸流的固體主體曲面之間的相對運動引起的。壓力與剪切力是透過流解 (輸出量) 求得的: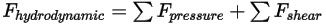
方程式 2.433
• 阻尼力 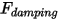 - 由摩擦阻尼作用引起的阻滯力。它是由固體物件的運動與使用者定義的阻尼係數
- 由摩擦阻尼作用引起的阻滯力。它是由固體物件的運動與使用者定義的阻尼係數 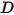 確定的:
確定的:
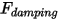 - 由摩擦阻尼作用引起的阻滯力。它是由固體物件的運動與使用者定義的阻尼係數
- 由摩擦阻尼作用引起的阻滯力。它是由固體物件的運動與使用者定義的阻尼係數 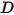 確定的:
確定的: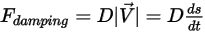
方程式 2.434
• 彈簧力 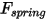 - 由弦
- 由弦 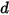 的位移、彈簧常數
的位移、彈簧常數 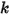 與彈簧預負載力
與彈簧預負載力 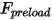 來確定:
來確定:
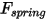 - 由弦
- 由弦 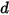 的位移、彈簧常數
的位移、彈簧常數 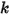 與彈簧預負載力
與彈簧預負載力 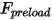 來確定:
來確定: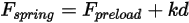
方程式 2.435
其中,彈簧位移 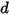 的定義如下:
的定義如下:
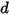 的定義如下:
的定義如下: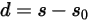
方程式 2.436
其中,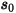 是先前位置
是先前位置 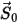 處位置向量
處位置向量 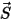 的量值。
的量值。
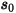 是先前位置
是先前位置 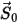 處位置向量
處位置向量 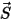 的量值。
的量值。• 摩擦力 - 採用接觸摩擦模型來解釋摩擦對動態系統的影響。摩擦力 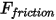 的建模如下:
的建模如下:
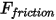 的建模如下:
的建模如下: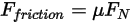
方程式 2.437
其中,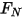 是施加於所關注固體曲面的接觸力的法向分量。針對摩擦係數
是施加於所關注固體曲面的接觸力的法向分量。針對摩擦係數 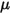 ,分別為靜止主體與移動主體引入靜態摩擦係數
,分別為靜止主體與移動主體引入靜態摩擦係數 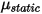 與滑動摩擦係數
與滑動摩擦係數 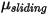 :
:
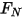 是施加於所關注固體曲面的接觸力的法向分量。針對摩擦係數
是施加於所關注固體曲面的接觸力的法向分量。針對摩擦係數 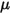 ,分別為靜止主體與移動主體引入靜態摩擦係數
,分別為靜止主體與移動主體引入靜態摩擦係數 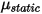 與滑動摩擦係數
與滑動摩擦係數 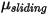 :
: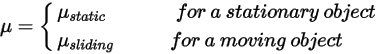
方程式 2.438
• 附加力 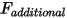 - 施加的使用者指定附加力。
- 施加的使用者指定附加力。
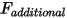 - 施加的使用者指定附加力。
- 施加的使用者指定附加力。1-DOF 旋轉
當任意旋轉軸由點 (軸中心) 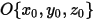 與方向單位向量
與方向單位向量 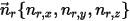 定義時,固體主體繞軸
定義時,固體主體繞軸 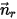 的旋轉也會降為 1 DOF 旋轉。同樣地,根據角動量守恆,方程式 2.427 也會沿切向方向變為純量方程式
的旋轉也會降為 1 DOF 旋轉。同樣地,根據角動量守恆,方程式 2.427 也會沿切向方向變為純量方程式 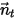 ,其定義如下:
,其定義如下:
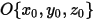 與方向單位向量
與方向單位向量 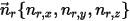 定義時,固體主體繞軸
定義時,固體主體繞軸 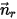 的旋轉也會降為 1 DOF 旋轉。同樣地,根據角動量守恆,方程式 2.427 也會沿切向方向變為純量方程式
的旋轉也會降為 1 DOF 旋轉。同樣地,根據角動量守恆,方程式 2.427 也會沿切向方向變為純量方程式 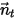 ,其定義如下:
,其定義如下: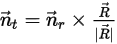
方程式 2.439
其中,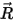 是從軸中心指向固體主體上任意點
是從軸中心指向固體主體上任意點 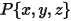 的向量:
的向量:
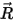 是從軸中心指向固體主體上任意點
是從軸中心指向固體主體上任意點 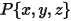 的向量:
的向量: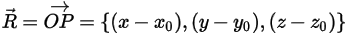
方程式 2.440
點 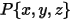 處的角速度和扭矩可改寫為:
處的角速度和扭矩可改寫為:
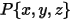 處的角速度和扭矩可改寫為:
處的角速度和扭矩可改寫為: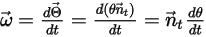
方程式 2.441
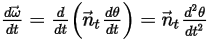
方程式 2.442
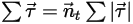
方程式 2.443
其中,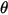 是點
是點 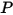 相對於起始或參照位置的旋轉角度。
相對於起始或參照位置的旋轉角度。
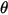 是點
是點 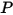 相對於起始或參照位置的旋轉角度。
相對於起始或參照位置的旋轉角度。如果慣性矩保持恆定,並且展開的扭矩項以顯性方式包含施加於旋轉體的所有扭矩,則所得純量角動量方程式的形式如下:
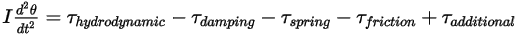
方程式 2.444
右邊扭矩項的定義如下:
• 流體動力扭矩 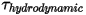 - 由於壓力與剪切力而產生的組合扭矩:
- 由於壓力與剪切力而產生的組合扭矩:
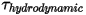 - 由於壓力與剪切力而產生的組合扭矩:
- 由於壓力與剪切力而產生的組合扭矩: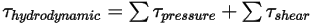
方程式 2.445
• 阻尼扭矩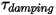 - 由旋轉速度
- 由旋轉速度 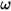 與使用者定義的阻尼係數
與使用者定義的阻尼係數 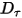 來確定:
來確定:
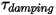 - 由旋轉速度
- 由旋轉速度 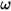 與使用者定義的阻尼係數
與使用者定義的阻尼係數 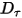 來確定:
來確定: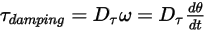
方程式 2.446
• 彈簧扭矩 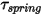 - 由扭轉引起的扭矩、位移角
- 由扭轉引起的扭矩、位移角 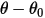 、使用者定義的預負載扭矩
、使用者定義的預負載扭矩 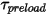 以及扭轉常數
以及扭轉常數 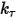 來確定。
來確定。
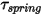 - 由扭轉引起的扭矩、位移角
- 由扭轉引起的扭矩、位移角 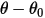 、使用者定義的預負載扭矩
、使用者定義的預負載扭矩 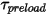 以及扭轉常數
以及扭轉常數 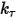 來確定。
來確定。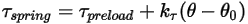
方程式 2.447
其中,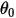 是參照角度。它通常是模型建構期間邊界或體積塊所在的方位,但可對應至不同的位置。例如,零角位移處的參照角度
是參照角度。它通常是模型建構期間邊界或體積塊所在的方位,但可對應至不同的位置。例如,零角位移處的參照角度 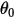 與初始角度位置處的參照角度不同。
與初始角度位置處的參照角度不同。
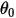 是參照角度。它通常是模型建構期間邊界或體積塊所在的方位,但可對應至不同的位置。例如,零角位移處的參照角度
是參照角度。它通常是模型建構期間邊界或體積塊所在的方位,但可對應至不同的位置。例如,零角位移處的參照角度 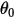 與初始角度位置處的參照角度不同。
與初始角度位置處的參照角度不同。• 摩擦扭矩 - 由兩個物件接觸移動時所產生的摩擦力引起的扭矩。在實驗中,它是由所施加的扭矩與觀測扭矩或凈扭矩之間的差異確定的。這具體取決於摩擦係數 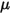 與施加於接觸曲面的法向力
與施加於接觸曲面的法向力 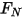 所引起的接觸扭矩:
所引起的接觸扭矩:
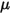 與施加於接觸曲面的法向力
與施加於接觸曲面的法向力 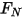 所引起的接觸扭矩:
所引起的接觸扭矩: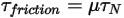
方程式 2.448
其中,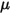 是一個使用者定義參數,其在方程式 2.438 中定義。
是一個使用者定義參數,其在方程式 2.438 中定義。
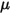 是一個使用者定義參數,其在方程式 2.438 中定義。
是一個使用者定義參數,其在方程式 2.438 中定義。• 附加扭矩 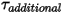 - 新增使用者指定的附加扭矩。
- 新增使用者指定的附加扭矩。
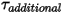 - 新增使用者指定的附加扭矩。
- 新增使用者指定的附加扭矩。反彈模型
在許多情況下,固體主體僅在有限的空間 (有限的距離或角度) 內進行平移和/或旋轉,即其處於最大值和/或最小值位置。例如,如下圖所示,當一個簡易重力擺錘以角度 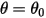 從原始位置釋放時,作用在其質量上的恢復力使其在平衡位置附近擺動。平衡位置
從原始位置釋放時,作用在其質量上的恢復力使其在平衡位置附近擺動。平衡位置 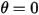 任意一側的最大角度取決於其釋放位置
任意一側的最大角度取決於其釋放位置 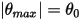 。如果不存在摩擦 (無摩擦樞軸及真空),則最大角度會保持不變,而擺錘會在相同的極值位置永久地來回擺動。但是,例如,當擺錘處於大氣中時,空氣阻力 (阻尼作用) 會導致最大擺角減小,並最終停止在平衡位置。
。如果不存在摩擦 (無摩擦樞軸及真空),則最大角度會保持不變,而擺錘會在相同的極值位置永久地來回擺動。但是,例如,當擺錘處於大氣中時,空氣阻力 (阻尼作用) 會導致最大擺角減小,並最終停止在平衡位置。
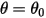 從原始位置釋放時,作用在其質量上的恢復力使其在平衡位置附近擺動。平衡位置
從原始位置釋放時,作用在其質量上的恢復力使其在平衡位置附近擺動。平衡位置 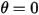 任意一側的最大角度取決於其釋放位置
任意一側的最大角度取決於其釋放位置 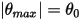 。如果不存在摩擦 (無摩擦樞軸及真空),則最大角度會保持不變,而擺錘會在相同的極值位置永久地來回擺動。但是,例如,當擺錘處於大氣中時,空氣阻力 (阻尼作用) 會導致最大擺角減小,並最終停止在平衡位置。
。如果不存在摩擦 (無摩擦樞軸及真空),則最大角度會保持不變,而擺錘會在相同的極值位置永久地來回擺動。但是,例如,當擺錘處於大氣中時,空氣阻力 (阻尼作用) 會導致最大擺角減小,並最終停止在平衡位置。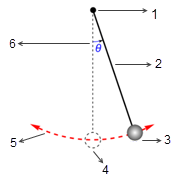
圖
1. 無摩擦樞軸
2. 無質量桿
3. 大擺錘
4. 平衡方位
5. 擺錘的軌跡
6. 幅度
此外,在擺動週期中,當擺錘到達最高位置 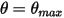 時,它會隨著其動能的總損失而變更方向。在此簡易重力擺錘中,動能會完全轉化為位能,而當考量介質阻力時,即會損失一部份動能來克服黏滯阻尼。但是,淨力或位能會驅動擺錘開始在背離平衡位置的方向上運動,而當處於平衡位置時,動能 (速度) 最大,勢能最小。在此情況下,
時,它會隨著其動能的總損失而變更方向。在此簡易重力擺錘中,動能會完全轉化為位能,而當考量介質阻力時,即會損失一部份動能來克服黏滯阻尼。但是,淨力或位能會驅動擺錘開始在背離平衡位置的方向上運動,而當處於平衡位置時,動能 (速度) 最大,勢能最小。在此情況下,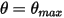 指示 1-DOF 角動量 (方程式 2.444 ) 的無反彈條件。
指示 1-DOF 角動量 (方程式 2.444 ) 的無反彈條件。
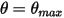 時,它會隨著其動能的總損失而變更方向。在此簡易重力擺錘中,動能會完全轉化為位能,而當考量介質阻力時,即會損失一部份動能來克服黏滯阻尼。但是,淨力或位能會驅動擺錘開始在背離平衡位置的方向上運動,而當處於平衡位置時,動能 (速度) 最大,勢能最小。在此情況下,
時,它會隨著其動能的總損失而變更方向。在此簡易重力擺錘中,動能會完全轉化為位能,而當考量介質阻力時,即會損失一部份動能來克服黏滯阻尼。但是,淨力或位能會驅動擺錘開始在背離平衡位置的方向上運動,而當處於平衡位置時,動能 (速度) 最大,勢能最小。在此情況下,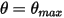 指示 1-DOF 角動量 (方程式 2.444 ) 的無反彈條件。
指示 1-DOF 角動量 (方程式 2.444 ) 的無反彈條件。除了無反彈條件之外,限制位置處的移動主體可能根本不會失去任何動能而發生反彈 (理想反彈),或僅會失去其部份動能 (部份反彈)。當對平移與旋轉的 1-DOF 動態方程式 (方程式 2.432 與方程式 2.444) 進行求解來確定固體主體或壁邊界在流域中的運動時,會套用下列三個反彈條件:
• 無反彈 - Creo Flow Analysis 中的預設模型。這會確定當固體主體或邊界到達其運動極限時,它會隨著其動能的總損失而變更方向。使用 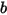 與
與  分別表示反彈和入射,以及
分別表示反彈和入射,以及 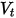 與
與 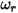 分別表示平移與旋轉速度 (僅限量值) 時,此反彈模型的表示如下:
分別表示平移與旋轉速度 (僅限量值) 時,此反彈模型的表示如下:
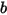 與
與  分別表示反彈和入射,以及
分別表示反彈和入射,以及 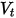 與
與 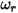 分別表示平移與旋轉速度 (僅限量值) 時,此反彈模型的表示如下:
分別表示平移與旋轉速度 (僅限量值) 時,此反彈模型的表示如下:◦ 平移
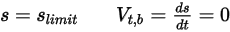
方程式 2.449
◦ 旋轉
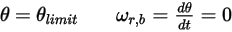
方程式 2.450
• 部份反彈 - 此模型規定,當固體主體或邊界到達其運動極限時,它會隨著其動能的部份損失 (由使用者指定的係數來確定,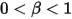 ) 而變更方向:
) 而變更方向:
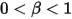 ) 而變更方向:
) 而變更方向:◦ 平移
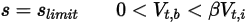
方程式 2.451
◦ 旋轉
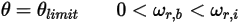
方程式 2.452
• 理想反彈 - 此模型規定,當固體主體或邊界到達其運動極限時,它會在無動能損失 (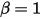 ) 的情況下變更方向:
) 的情況下變更方向:
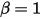 ) 的情況下變更方向:
) 的情況下變更方向:◦ 平移

方程式 2.453
◦ 旋轉

方程式 2.454