空蝕模型
在 Creo Flow Analysis 中,與在由 Singhal 等人 開發的原始模型中一樣,空蝕流中的工作流體始終假設為液體、蒸汽與某些不凝結氣體的混合流。依預設,空蝕模型會考慮液汽相變以及不凝結氣體的影響。根據針對不凝結氣體效應的建模方法,下表提供了五個不同的模型以供預測液體系統中的曝氣與空蝕。本節詳細介紹這些模型。
|
NCG 模型
|
描述
|
|---|---|
|
恆定氣體質量分數
|
(不凝結氣體) NCG 的質量分數恆定,可將其視為具有微小可壓縮氣泡的不溶性氣體
|
|
可變氣體質量分數
|
與恆定氣體質量分數模型類似,但 NCG 的質量分數是可變的,例如入口可以引入不同的質量分數
|
|
平衡溶解氣體模型
|
液體中溶解的 NCG 的質量分數等於平衡值
|
|
溶解氣體模型
|
液體中溶解的 NCG 的質量分數取決於吸收或解吸率以及平衡值
|
|
完整氣體模型
|
組合溶解氣體模型與可變氣體質量分數
|
恆定氣體質量分數模型
恆定氣體質量分數模型是 Creo Flow Analysis 中的基本或預設空蝕模型。它基於 Singhal 等人取得的成果。此模型假設在工作流體中,液體中先前存在的不凝結氣體 (NCG) 會變為不可溶解氣體或遵循理想氣體定律的自由氣泡。雖然預先規定的所有不凝結氣體都會隨著空蝕區域內壓力的減小而自由膨脹,但是會預先規定不凝結氣體的質量分數,使其在空蝕流中保持不變:
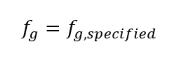
方程式 2.217
其中 fg,specified 是使用者指定的值。
不凝結氣體的密度遵循理想氣體定律:
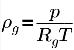
方程式 2.218
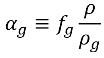
方程式 2.219
雖然 NCG 的質量分數固定,通常在天然水等中具有極小的值 (通常為 1.5e-05 或 15 ppm),但是其體積分數 αg 會有所不同,可以是相當大的值。在孔穴或低壓力區域中,不凝結氣體會與蒸汽爭先填充空間內的空泡,具體取決於氣體與蒸汽密度。
針對液汽質量傳遞,會基於方程式 2.194 和方程式 2.195 建構蒸汽質量分數方程式 2.169 中的空蝕源項與匯項。具體而言,需要使用氣泡增長與塌陷期間的已知流動量估計氣泡半徑 RB。Singhal 等人 認為,如果典型氣泡大小 RB 與極限 (可能的最大) 氣泡大小相同,則可根據氣動阻力與表面張力之間的平衡確定 RB。核子工業使用的關係式如下:
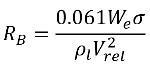
方程式 2.220
其中 Vrel 為液汽相對速度的量值。在氣泡流態 (發生空蝕) 下,Vrel 較小,通常約為液體速度的 5-10%。透過將不同極限引數 (例如 RB →0) 用作 αv →0 並基於單位體積的相變率與提供相的體積分數 (或質量分數) 成比例這一事實,可取得蒸汽產生/凝結率的下列運算式,以完成空蝕模型︰
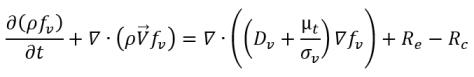
方程式 2.221
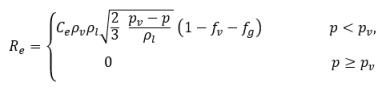
方程式 2.222
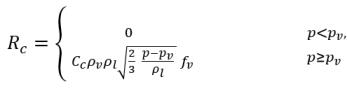
方程式 2.223
其中 Ce 與 Cc 是蒸發與凝結係數,二者可以是使用者指定的常數值 (依預設設定為 1.0) 或已知流動量的函數。在 方程式 2.222 和方程式 2.223 中,引入了新臨界壓力 ρv 以取代方程式 2.194 與方程式 2.195 中的飽和蒸汽壓力 ρsat。根據 Singhal 等人 的研究,為了解釋亂流對空蝕流的影響 (透過試驗研究觀察),將 Hinze 指定的亂流壓力波動局部值:
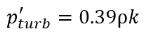
方程式 2.224
加到飽和蒸汽壓力上,以將相變臨界壓力值提高到:
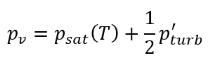
方程式 2.225
針對層流,pv=psat(T)
當考慮熱傳並且所有相密度 (包括液體、蒸汽與不凝結氣體) 會隨溫度發生變化時,飽和蒸汽壓力 psat 也是溫度的函數。因此,在此空蝕模型中可以考慮對空蝕的直接熱效應。
可變氣體質量分數模型
可變氣體質量分數模型假設不凝結氣體總是保持為無法溶解到液體中的自由氣體,但質量分數不再是預先規定的常數,這與恆定氣體質量分數模型不同。相反地,局部質量分數的分佈由傳輸方程式控制。而液汽質量傳遞透過方程式 2.221、方程式 2.222 及方程式 2.223 中參照的相同空蝕模型進行建模。為清楚起見,完整的建模方程式組如下所示:
• 液汽相變
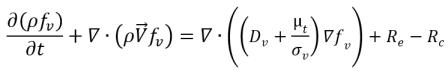
方程式 2.226
其中
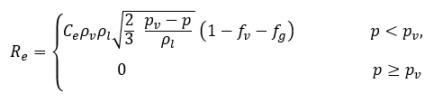
方程式 2.227
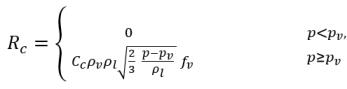
方程式 2.228
• 不凝結氣體傳輸方程式
根據方程式 2.199,不凝結氣體 (fg) 的傳輸方程式如下:
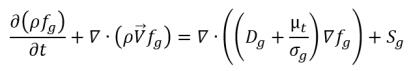
方程式 2.229
其中 Sg 是不凝結氣體的外部或使用者定義的源。
平衡溶解氣體模型
在空蝕流中,流體中的不凝結氣體可以在液體中溶解或釋放,以實現液相與氣相之間的質量濃度動態平衡。平衡溶解氣體模型假設總不凝結氣體的質量分數保持為常數。但一部分氣體會溶解到液體中以立即滿足局部平衡條件。在數學方面,除了蒸汽質量分數方程式和蒸汽質量傳遞模型相同之外,還會求解溶解氣體質量分數 fgd (假設始終處於平衡狀態) 的其他傳輸方程式。建模方程式如下所示:
• 液汽相變
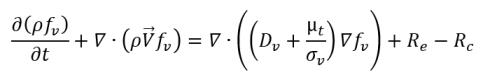
方程式 2.230
其中
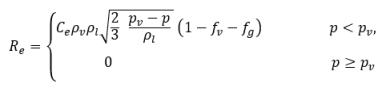
方程式 2.231
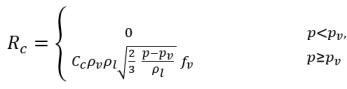
方程式 2.232
• 氣體吸收/溶解或釋放
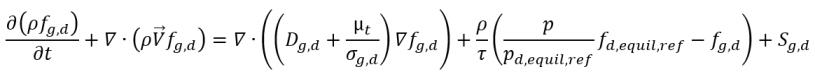
方程式 2.233
其中
Sg,d | 使用者定義的氣體溶解或釋放定律 |
fd,equil,ref | 在參照壓力 pd,equil,ref 下溶解氣體的平衡質量分數 |
fd,equil,ref 和 pd,equil,ref | 使用者指定的值 |
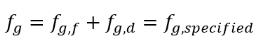
方程式 2.234
其中 fg,specified 是使用者指定的值。
溶解氣體模型
此模型對液體中的溶解氣體始終處於平衡狀態這一條件進行了放寬。溶解氣體質量分數 (fg,d) 取決於成分傳輸與溶解或釋放率 (有限率),而不是由瞬時質量傳遞的平衡條件決定。因此,溶解氣體模型與平衡溶解氣體模型共用相同的建模公式,方程式 2.230 - 方程式 2.234。不過,氣體溶解與釋放的有限質量傳遞率使用不同的時間尺度 (Γ) 進行表徵。針對在液體中吸收或溶解的氣體,會根據指定的吸收時間 (依預設,溶解氣體的溶解時間為 10 s) 指定 Γ。而針對液體中溶解氣體的釋放,會根據指定的氣體釋放時間 (根據預設 Γ,溶解氣體的釋放時間為 10 s) 規定質量傳遞率。
完整氣體模型
完整氣體模型是溶解氣體模型與可變氣體模型的組合。不凝結氣體的質量分數會隨著時間與空間而發生變化,而不凝結氣體也可能發生氣體溶解或吸收與釋放。完整的建模方程式組如下所示:
• 液汽相變
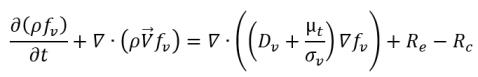
方程式 2.235
其中
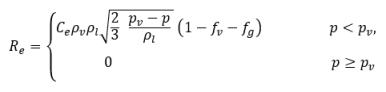
方程式 2.236
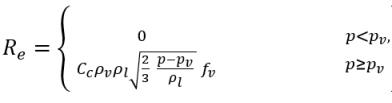
方程式 2.237
• 不凝結氣體之傳輸
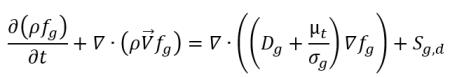
方程式 2.238
• 氣體溶解或釋放
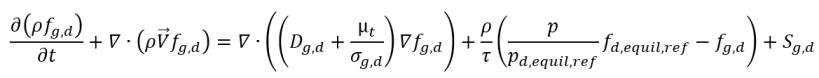
方程式 2.239