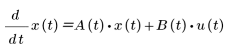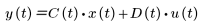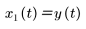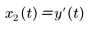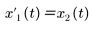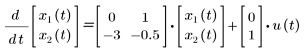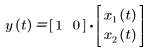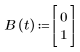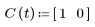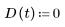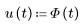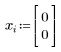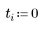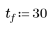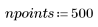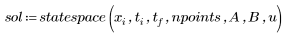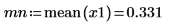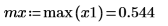任務 3 - 1:建立狀態空間下的 ODE 模型
請閱讀以下定義的問題,然後在任務 3 - 1 到任務 3 - 3 中,使用下列方法求解:
• 狀態空間 ODE 求解器
• ODE 求解器
• 解題指令群
問題定義
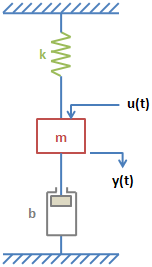
考量到正統質量彈簧阻尼系統:
此方程組的動態方程式由下列方程式提供:
您可使用以下列格式表現的狀態空間模型,表示此系統:
其中:
• A - 狀態矩陣
• B - 輸入矩陣
• C - 輸出矩陣
• D - 直接傳輸矩陣
• x - 狀態向量
• u - 輸入
• y - 量測或控管的輸出
| 您可將狀態和建立系統動態模型之輸出非線性方程組加以線性化,以取得上述線性系統。 |
對此二階系統使用兩個狀態變數。
假設 m = 1、b = 0.5 且 k = 3,則系統方程組如下:
此模型以狀態空間矩陣的格式撰寫如下:
狀態空間 ODE 求解器
1. 定義矩陣函數 A、B、C 及 D。
2. 將輸入定義成為 heaviside 階梯函數。若要插入階梯函數,請鍵入 F,再按 Ctrl+G。
3. 定義兩個變數的初始條件。若要鍵入 i 作為文字下標,請在「數學」標籤的「樣式」群組中,按一下「下標」,然後鍵入 i。
4. 定義要求解方程組的時間邊界。
5. 定義要求解的點數,排除 ti。
6. 呼叫 statespace 函數。
矩陣 sol 的第一欄包含求得解的時間。其餘的欄包含那時的狀態變數 x1 及 x2。
7. 從矩陣 sol 萃取 t、x1 及 x2。
8. 計算 x1 的平均值與最大值。
9. 繪製一段時間的 x1,並使用標記顯示其平均值與最大值。
繪圖可顯示暫態回應特性,例如上升時間、過衝及安定時間。