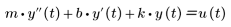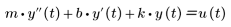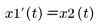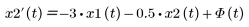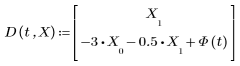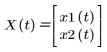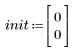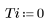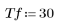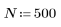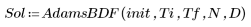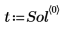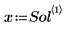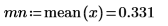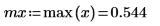任務 3 - 2:利用 ODE 求解器求解 ODE
在上個任務中,使用狀態空間 ODE 求解器,求解了質量彈簧阻尼系統。您也可以使用 ODE 求解器求解此問題。舉原先的動態方程式為例:
系統參數原先為 m = 1、b = 0.5 且 k = 3。此輸入原先為 heaviside 階梯函數 u(t) = Φ(t)。您可以根據一階 ODE 重寫二階方程式:
1. 定義指定系統右側的向量函數。
D 的引數為 t、自變數及 X (因變數的向量):
2. 定義 x1 及 x2 的初始值。
3. 定義計算解的初始與最終時間。
4. 定義時間步距數。
5. 呼叫 AdamsBDF 求解器以計算解。
◦ AdamsBDF 求解器是混合求解器。它從非剛性 Adams 求解器開始。它若視此為剛性問題,則會切換至剛性 BDF 求解器。
◦ 或者,可以其他的 ODE 求解器取代 AdamsBDF 求解器。如需詳細資訊,請參閱「說明」的「關於微分方程式求解器」主題。
◦ 解為具有每個 N 步距之系統時間、位移及速度的 3 欄矩陣:
6. 從 Sol 萃取時間及位移,並繪製其關係圖。
7. 計算 x 的平均值與最大值。
8. 繪製一段時間的 x,並使用標記顯示其平均值與最大值。
繪圖可顯示暫態回應特性,例如上升時間、過衝及安定時間。