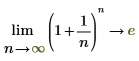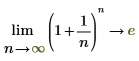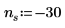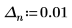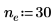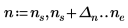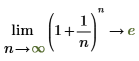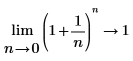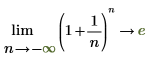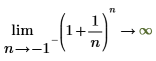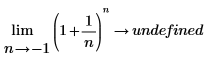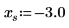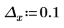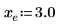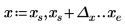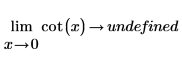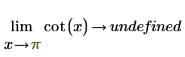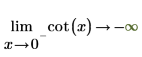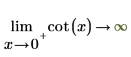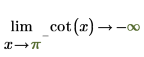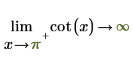範例︰使用極限運算子
使用無限大作為限制值
1. 使用極限運算子,並以符號方式計算當期引數接近無限大時的運算式。
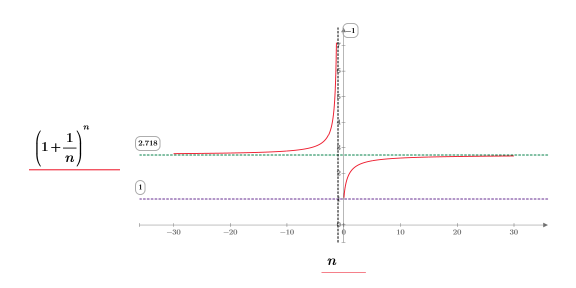
2. 繪製函數以促進其視覺化。使用水平標記來表示 e。
在 (x, y) 象限中,我們觀察下列項目︰
◦ 隨著 n 逐漸接近 positive infinity,函數將接近 y=e。
◦ 隨著 n 逐漸接近 0,函數將接近 y=1。
在進行數學運算時,這會以下列符號計算來表示︰
在 (-x, y) 象限中,我們觀察下列項目︰
◦ 隨著 n 逐漸接近 negative infinity,函數將接近 y=e。
◦ 隨著 n 逐漸接近 -1,函數將接近 y=infinity。
在進行數學運算時,這會以下列符號計算來表示︰
| 使用第二個方程式中的左側極限方向,表示將從曲線的左側接近 -1。如果未指定,則因為未針對 -1 < n < 0 定義函數,因此計算將會傳回「未定義」: |
使用極限方向
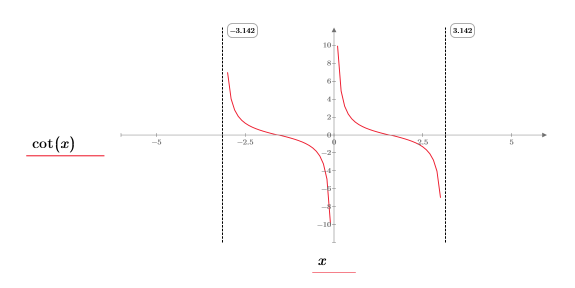
1. 繪製 cot 函數。
在 (x, y) 象限中,我們觀察下列項目︰
◦ 隨著 x 逐漸接近 0,函數將接近 y=infinity。
◦ 隨著 x 逐漸接近 π,函數將接近 y=-infinity。
在進行數學運算時,這會以下列符號計算來表示︰
由於此函數相對於 x=+/- n*π/2 對稱,因此符號計算會傳回「未定義」,這是因為圍繞 x=0 的函數 (與任意多個 π) 可以是 infinity 或 -infinity,取決於 x 接近 0 的方向。
這是指定「極限方向」的較好方法。
2. 指定「極限方向」,然後以符號方式重新計算圍繞 0 與 π 的 cot 函數。
傳回的結果與繪圖相符。
| 有時它有助於繪製函數,以實現其視覺化,以及檢驗符號計算結果的有效性。 |