変数についての仮説を立てる
キーワード assume および 1 つまたは複数の変更式を使用して、シンボリック式における変数の領域 (実数に制限するなど) についての仮説を立てます。assume の後に挿入できる変更式のタイプは次のとおりです。
|
変更式
|
仮説
|
|---|---|
|
x=real
|
x は実数です。
|
|
x=complex
|
x は複素数です。
|
|
x=integer
|
x は整数です。
|
|
x>a
|
x は a よりも大きい実数です。
|
|
x≥a
|
x は a 以上の実数です。
|
|
x<b
|
x は b 未満の実数です。
|
|
x≤b
|
x は b 以下の実数です。
|
|
x=RealRange(a, b)
|
x は a<x<b (ここで a<b) の実数です。
|
|
n=even
|
n は偶数の整数です。
|
|
n=odd
|
n は奇数の整数です。
|
先行するリストで等式を指定するには、論理演算子の等号を使用します。
変数には次の規則が適用されます。
• 複数のキーワードの後に assume を挿入した場合、変数についての仮説は最初のキーワードで実行される演算に適用されます。
• キーワード assume は割り当てや代入を行いません。これを行うには、変数を定義するかキーワード substitute を使用します。
• 数値的に定義された変数を除外または代入するには、キーワード explicit を使用します。キーワード assume は PTC Mathcad で解を求める領域にはほとんど制約を与えないので、簡素化とシンボリックな積分でよく使用されます。
• デフォルトでは、Mathcad 内の変数はすべて実数です。変数が複素数であることを示すには、complex 変更因子を使用します。



• Mathcad は、関数外の変数 t だけが複素数であることを前提としています。
• 関数内の変数を含むすべての t 変数が複素数であることを示すには、All 変更因子を使用します。

例
• x の領域を実数に制限するには、次のようにします。
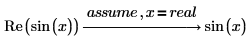
• x の領域を複素数に制限するには、次のようにします。

• 式における 2 つ以上の変数の領域を制限するには、コンマで区切った変更式のリストを assume キーワードの後ろに次のように挿入します。

• 式におけるすべての変数の領域を制限するには、変更式に変更因子 ALL を挿入します。
