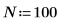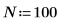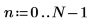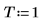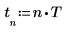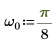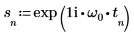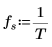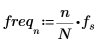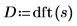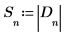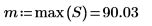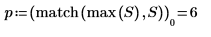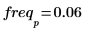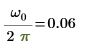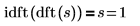Ejemplo: DFT de funciones complejas
Utilice las funciones dft y idft para calcular las transformadas de Fourier directas o inversas, complejas o reales.
1. Cree varios datos complejos simulados con N puntos de datos:
2. Defina el espaciado de muestreo.
3. Utilice la función exp para definir la siguiente señal.
4. Defina la frecuencia de muestreo y la frecuencia correspondiente a la entrada de orden n en el vector transformado.
5. Aplique la función dft para transformar los datos en el dominio de frecuencias.
6. Guarde la magnitud de los elementos del array D en un nuevo array.
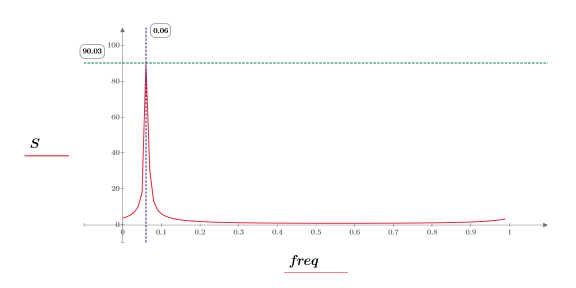
7. Utilice las funciones match y max para calcular la amplitud y la frecuencia del pico.
8. Trace la magnitud de DFT como una función de frecuencia.
9. Muestre que la frecuencia del valor pico se corresponde con ω0/2π.
10. Utilice la función idft para mostrar que la IDFT de DFT de una señal devuelve la señal en sí.